【培优分级练】北师大版数学九年级上册 第一次月考试卷02（含解析）

这是一份【培优分级练】北师大版数学九年级上册 第一次月考试卷02（含解析），文件包含北师大版2022-2023学年九年级上册第一次月考试卷02解析版docx、北师大版2022-2023学年九年级上册第一次月考试卷02原卷版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。
北师大版2022-2023学年九年级上册第一次月考试卷02
一、单选题
1．下列方程中，一定是一元二次方程的是（        ）
A． B． C． D．
【答案】C
【解析】
【分析】
根据“只含有一个未知数，并且未知数的最高次数是2的整式方程：进行判断即可．
解：A、当a=0时， 不是一元二次方程，故本选项不符合题意．
B、该方程含有2个未知数，不是一元二次方程，故本选项不符合题意．
C、该方程符合一元二次方程的定义，故本选项符合题意．
D、该方程不是整式方程，不是一元二次方程，故本选项不符合题意．
故选C．
【点睛】
本题主要考查了一元二次方程，判断一个方程是否是一元二次方程应注意抓住5个方面：“化简后”；“一个未知数”；“未知数的最高次数是2”；“二次项的系数不等于0”；“整式方程”．
2．下列命题中，是真命题的是（   ）
A．对角线互相垂直的四边形是菱形 B．对角形相等的四边形是矩形
C．顺次连结平行四边形各边中点所得四边形是平行四边形 D．一组邻边相等的平行四边形是正方形
【答案】C
【解析】
【分析】
根据菱形、矩形、平行四边形、正方形的判定定理逐项判断即可．
解：A. 对角线互相垂直的平行四边形是菱形，此选项不符合题意；
B. 对角形相等的平行四边形是矩形，此选项不符合题意；
C. 顺次连结平行四边形各边中点所得四边形是平行四边形       ，此选项符合题意；
D. 一组邻边相等的矩形是正方形，此选项不符合题意；
故选：C．
【点睛】
本题考查的知识点是菱形、矩形、平行四边形、正方形的判定定理，熟记菱形、矩形、平行四边形、正方形的判定定理内容是解此题的关键．
3．下面结论错误的是（ ）
A．方程，则，
B．方程有实根，则
C．方程可配方得
D．方程两根，
【答案】A
【解析】
【分析】
A、根据根与系数的关系和根的判别式即可得到结论；B、由根的判别式即可得到结论；C、把原方程配方后可得结果；D、解方程即可得到结论；
解：A、方程x2+4x+5=0，∵△=42-4×5＜0，则方程无实数根，此选项错误；
B、∵方程2x2-3x+m=0有实根，∴△=9-8m≥0，∴m≤，此选项正确；
C、方程x2-8x+1=0可配方得（x-4）2=15，此选项正确；
D、解方程x2+x-1=0得x1=，x2=，此选项正确；
故选A．
【点睛】
本题考查了根与系数的关系，根的判别式，配方法解一元二次方程，公式法解一元二次方程，熟练掌握各知识点是解题的关键．
4．取一张长与宽之比为5:2的长方形纸板，剪去四个边长为的小正方形（如图），并用它做一个无盖的长方体形状的包装盒．要使包装盒的容积为（纸板的厚度略去不计），问这张长方形纸板的长与宽分别为多少厘米？若设这张长方形纸板的长为厘米，则由题意可列出的方程是（       ）

A． B．
C． D．
【答案】C
【解析】
【分析】
根据题意设这张长方形纸板的长为5x cm，宽为2x cm，进而表示出长方体的底面积，即可表示出长方体体积，进而得出等式求出答案．
解：设这张长方形纸板的长为5x cm，宽为2x cm，根据题意可得：
；
故选：C．
【点睛】
此题主要考查了一元二次方程的应用，根据题意正确表示出长方体的底面积是解题关键．
5．如图，菱形的对角线，相交于点，是的中点，，则菱形的周长为（   ）

A．8 B． C．16 D．20
【答案】C
【解析】
【分析】
由菱形的性质可得出，，再根据直角三角形斜边上的中线等于斜边的一半得出的长，结合菱形的周长公式即可得出结论．
解：四边形为菱形，
，，
为直角三角形．
，且点为的中点，
．
．
故选：C．
【点睛】
本题考查了菱形的性质以及直角三角形的性质，解题的关键是求出．本题属于基础题，难度不大，解决该题型题目时，根据菱形的性质得出对角线互相垂直，再通过直角三角形的性质得出菱形的一条边是关键．
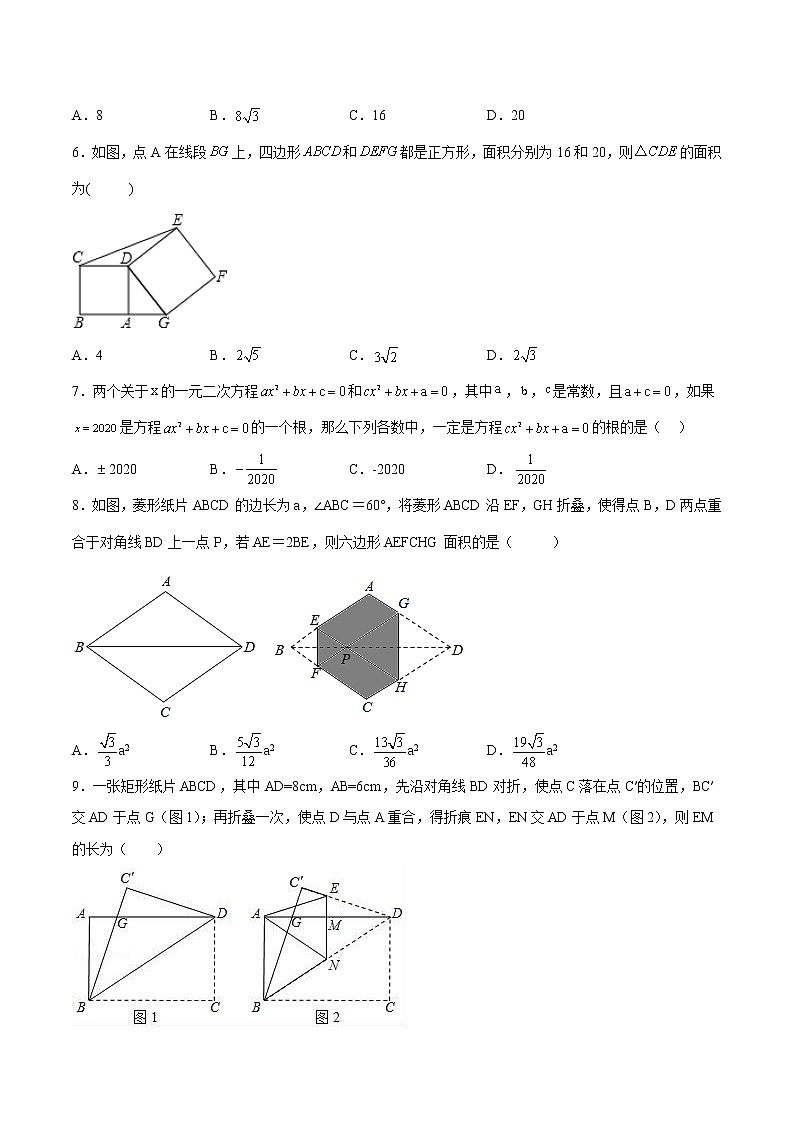
6．如图，点A在线段上，四边形和都是正方形，面积分别为16和20，则的面积为(       )

A．4 B． C． D．
【答案】A
【解析】
【分析】
过点E作EH⊥CD，交CD的延长线与H，由题意可证△ADG≌△，即可得EH=AG=，从而可求△CDE的面积．
解：如图：过点E作EH⊥CD，交CD的延长线与H．

∵四边形ABCD和四边形DEFG都是正方形，面积分别是和，
∴AD⊥CD，，∠BAD=90°，，
在Rt△ADG中，
∵∠ADG+∠GDH=90°，∠DGH+∠EDH=90° ，
∴∠EDH=∠ADG，且∠DAG=∠H=90°，DE=DG
∴△ADG≌△
∴EH=AG=,
∴
故选：
【点睛】
本题考查的是正方形的性质，三角形全等的判定与性质，勾股定理的应用，掌握以上知识是解题的关键．
7．两个关于的一元二次方程和，其中，，是常数，且，如果是方程的一个根，那么下列各数中，一定是方程的根的是（   ）
A．2020 B． C．-2020 D．
【答案】C
【解析】
【分析】
根据一元二次方程的定义以及一元二次方程的解法即可求出答案．
∵，，a+c=0
∴，
∵ax2+bx+c=0 和cx2+bx+a=0，
∴，，
∴，，
∵是方程的一个根，
∴是方程的一个根，
∴是方程的一个根，
即是方程的一个根
故选：C．
【点睛】
本题考查了一元二次方程，解题的关键是熟练运用一元二次方程的定义以及方程的解的概念．
8．如图，菱形纸片ABCD的边长为a，∠ABC＝60°，将菱形ABCD沿EF，GH折叠，使得点B，D两点重合于对角线BD上一点P，若AE＝2BE，则六边形AEFCHG面积的是（       ）

A．a2 B．a2 C．a2 D．a2
【答案】C
【解析】
【分析】
由菱形的性质可得AC⊥BD，∠BAD＝120°，AB＝BC＝a，AE＝，BE＝a，∠ABD＝30°，由折叠的性质可得EF⊥BP，∠BEF＝∠PEF，BE＝EP＝a，可证△BEF是等边三角形，△GDH是等边三角形，四边形AEPG是平行四边形，可得AG＝EP＝a，即可求DG的长，由面积和差可求解．
解：如图，连接AC，

∵四边形ABCD是菱形，∠ABC＝60°，AE＝2BE，
∴AC⊥BD，∠BAD＝120°，AB＝BC＝a，AE＝，BE＝a，∠ABD＝30°，
∴AC＝AB＝BC＝a，BD＝a，
∵将菱形ABCD沿EF，GH折叠，
∴EF⊥BP，∠BEF＝∠PEF，BE＝EP＝a，
∴EF∥AC，
∴，
∴BE＝BF，
∴△BEF是等边三角形，
∴∠BEF＝60°＝∠PEF，
∴∠BEP＝∠BAD＝120°，
∴EH∥AD，
同理可得：△GDH是等边三角形，GP∥AB，
∴四边形AEPG是平行四边形，
∴AG＝EP＝a，
∴DG＝a，
∴六边形AEFCHG面积＝S菱形ABCD﹣S△BEF﹣S△GDH＝•a•a﹣×（a）2﹣×（a）2＝a2，
故选：C．
【点睛】
本题考查了翻折变换，菱形的性质，平行四边形的判定和性质，等边三角形的性质判定等知识，求出DG的长是本题的关键．
9．一张矩形纸片ABCD，其中AD=8cm，AB=6cm，先沿对角线BD对折，使点C落在点C′的位置，BC′交AD于点G（图1）；再折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M（图2），则EM的长为（　　）

A．2 B． C． D．
【答案】D
【解析】
∵点D与点A重合，得折痕EN，
∴DM=4cm，
∵AD=8cm，AB=6cm，
在Rt△ABD中,BD==10cm，
∵EN⊥AD，AB⊥AD，
∴EN∥AB，
∴MN是△ABD的中位线，
∴DN=BD=5cm，
在Rt△MND中，
∴MN==3(cm)，
由折叠的性质可知∠NDE=∠NDC，
∵EN∥CD，
∴∠END=∠NDC，
∴∠END=∠NDE，
∴EN=ED，设EM=x，则ED=EN=x+3，
由勾股定理得ED²=EM²+DM²,即(x+3) ²=x²+4²，
解得x=,
即EM=cm．
故选D．
10．对于一元二次方程，下列说法：
①若，则；
②若方程有两个不相等的实根，则方程必有两个不相等的实根；
③若是方程的一个很，则一定有成立；
④若是一元二次方程的根，则．
其中正确的（       ）
A．①② B．①②④ C．①②③④ D．①②③
【答案】B
【解析】
【分析】
按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论，可得答案．
解：①若，则是方程的解，
由一元二次方程的实数根与判别式的关系可知：，故①正确；
②方程有两个不相等的实根，
，
，
则方程的判别式，
方程必有两个不相等的实根，故②正确；
③是方程的一个根，
则，
，
若，等式仍然成立，
但不一定成立，故③不正确；
④若是一元二次方程的根，
则由求根公式可得：，，
，
，故④正确．
故正确的有①②④，
故选：B．
【点睛】
本题考查了一元二次方程根的判别式，灵活运用根的判别式是解题的关键．
二、填空题
11．写一个二次项系数为2的一元二次方程，使得两根分别是-2和1_______．
【答案】2x2＋2x−4＝0．
【解析】
【分析】
设方程为ax2＋bx＋c＝0，则由已知得出a＝2，根据根与系数的关系得，−2＋1＝，−2×1＝，求出即可．
解：∵二次项系数为2的一元二次方程的两个根为−2，1，
∴设方程为2x2＋bx＋c＝0，−2＋1＝，−2×1＝，
∴b=2，c=-4，
故答案为：2x2＋2x−4＝0．
【点睛】
本题考查了根与系数的关系：x1，x2是一元二次方程ax2＋bx＋c＝0（a≠0）的两根时，x1＋x2＝，x1x2＝．
12．顺次连结一个矩形各边的中点所得到的四边形是一个______．
【答案】菱形
【解析】
【分析】
根据三角形的中位线定理和菱形的判定定理解答．
解：如图，矩形ABCD中，E、F、G、H分别是AB，BC，CD，AD的中点，
连接AC，BD，
∵四边形ABCD是矩形，
∴AC=BD，
∵E，F，G，H分别为矩形各边的中点，
∴EH=BD，
同理：FG=BD，HG=AC，EF=AC，
∴EH=HG=GF=FE，
∴平行四边形EFGH是菱形，
故答案为：菱形．

【点睛】
本题考查的是菱形的判定、矩形的性质，掌握三角形的中位线定理和矩形的性质定理是解题关键．
13．某校八年级组织篮球赛，若每两班之间赛一场，共进行了28场，则该校八年级有____个班级．
【答案】8
【解析】
【分析】
设八年级有x个班，根据“各班均组队参赛，赛制为单循环形式，且共需安排15场比赛”，即可得出关于x的一元二次方程，解之取其正值即可得出结论．
解：设八年级有x个班，
依题意得：x（x-1）=28，
整理得：x2-x-56=0，
解得：x1=8，x2=-7（不合题意，舍去）．
则该校八年级有8个班级．
故答案为：8．
【点睛】
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
14．如图，在菱形ABCD中，AB＝8，∠B＝60°，点E在边AD上，且AE＝3．若过点E的直线l，将该菱形的面积平分，且与菱形的另一边交于点F，则线段EF的长为_____．

【答案】
【解析】
【分析】
根据全等图形的面积相等，在BC上截取CF=AE=3，连接EF，则EF即为所求，过点A作AH⊥BC，垂足为H，过点E作EG⊥BC，垂足为G，求得AH，FG，即可求得EF的长．
根据全等图形的面积相等，在BC上截取CF=AE=3，连接EF，则EF即为所求，过点A作AH⊥BC，垂足为H，
∵菱形ABCD中，AB＝8，∠B＝60°，
∴∠BAH＝30°，BH=4，AH==；
过点E作EG⊥BC，垂足为G，
∵四边形ABCD是菱形，
∴AD∥BC，
∵AH⊥BC，EG⊥BC，
∴AH=EG，AE=HG=3，
∴AH=EG=，AE=HG，
∵BH=4，BF=5，HG=3，
∴FG=BH+HG-BF=4+3-5=2，
∴EF==．
故答案为：．

【点睛】
本题考查了菱形的性质，勾股定理，熟练构造平行线间的距离，构造直角三角形是解题的关键．
15．已知关于x的方程，在内有两个不相等的实数根，则n的取值范围是___________________________．
【答案】-7＜n≤-5
【解析】
【分析】
根据“方程有两个不相等的实数根”求出n＞-7，解出方程，根据在内有两个不相等的实数根，求出n的取值，问题得解．
解：原方程整理得，
∴，
∵方程有两个不相等的实数根，
∴
∴n＞-7，
∴
∵方程在内有两个不相等的实数根，
∴，
解得n≤-5，n≤11，
∴n≤-5，
又∵n＞-7，
∴-7＜n≤-5．
故答案为：-7＜n≤-5
【点睛】
本题考查了含字母系数的一元二次方程，根的判别式，综合性较强，解题的关键是用公式法求出一元二次方程的两个根，根根据题意列出不等式．
16．某商场销售一批衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，商场采取了降价措施．假设在一定范围内，衬衫的单价每降1元，商场平均每天可多售出2件．如果降价后商场销售这批衬衫每天盈利1250元，那么衬衫的单价降了多少元？设衬衫的单价降了x元，则可列方程为__________________．
【答案】（40﹣x）（20+2x）＝1250
【解析】
【分析】
设衬衫的单价降了x元．根据题意等量关系：降价后的销量×每件的利润=1250，根据等量关系列出方程即可．
设衬衫的单价降了x元．根据题意，得(40﹣x)(20+2x)＝1250
故答案：（40﹣x）（20+2x）＝1250
【点睛】
此题主要考查了一元二次方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程．
17．如图，在矩形ABCD中， AB＝3，AD＝10，点E在AD上且DE＝2．点G为AE的中点，点P为BC边上的一个动点，F为EP的中点，则GF＋EF的最小值为______．

【答案】5
【解析】
【分析】
首先证明GF+EF=       （PA+PE），求出PA+PE的最小值即可，作点A关于BC的对称点T，连接ET交BC于P′，此时P′E+P′A的值最小．
解：如图，连接PA．

∵AG=EG，EF=FP，
∴GF=PA，
∴GF+EF=（PA+PE），
求出PA+PE的最小值即可，
作点A关于BC的对称点T，连接ET交BC于P′，此时P′E+P′A的值最小，
∵四边形ABCD是矩形，
∴∠EAT=90°，
∵AB=BT=3，
∴AT=6，
∵AD=10，DE=2，
∴AE=AD-DE=10-2=8，
∴P′E+P′A=P′E+P′T=ET=，
∴EG+EF的最小值为×10=5，
故答案为5．
【点睛】
本题考查轴对称-最短问题，三角形中位线定理，矩形的性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用轴对称解决最短问题．
18．如果关于x的一元二次方程有两个实数根，且其中一个根为另外一个根的2倍，则称这样的方程为“倍根方程”，以下关于“倍根方程”的说法，正确的有_____（填序号）．
①方程是“倍根方程”；
②若是“倍根方程”，则；
③若满足，则关于x的方程是“倍根方程”；
④若方程是“倍根方程”，则必有．
【答案】②③④
【解析】
【分析】
①求出方程的根，再判断是否为“倍根方程”；
②根据“倍根方程”和其中一个根，可求出另一个根，进而得到m，n之间的关系；
③当满足时，有，求出两个根，再根据代入可得两个根之间的关系，讲而判断是否为“倍根方程”；
④用求根公式求出两个根，当或时，进一步化简，得出关系式，进行判断即可．
①解方程，得，
，
方程不是“倍根方程”．故①不正确；
②是“倍根方程”，且，
因此或．
当时，，
当时，，
，故②正确；
③，
，
，
，
因此是“倍根方程”，故③正确；
④方程的根为，
若，则，
即，
，
，
，
，
，
若，则，
，
，
，
，
．故④正确，
故答案为：②③④．
【点睛】
本题考查了解一元二次方程以及一元二次方程的求根公式，新定义的倍根方程的意义，理解倍根方程的意义和正确求出方程的解是解决问题的关键．
三、解答题
19．用配方法解下列方程：
（1）；
（2）；
（3）；
（4）；
（5）；
（6）．
【答案】（1）；（2）原方程无实数根；（3）；（4）；（5）；（6）．
【解析】
【分析】
（1）方程两边加上1，再进行配方即可求解；
（2）移项后，方程两边都加上一半的平方，再进行配方即可求解；
（3）先将方程的二次项系数化为1，再进行配方即可求解；
（4）先将方程的二次项系数化为1，再进行配方即可求解；
（5）先将方程整理后，再进行配方即可求解；
（6）先将方程整理后，再进行配方即可求解．
（1）

配方，得，
．
（2）
移项，得．
配方，得．
，
原方程无实数根．
（3）
移项，得．
配方，得，
．
（4）
移项，得．
配方，得，
．
（5）
原方程化为一般形式为．
移项，得．
配方，得，
．
（6）
原方程化为一般形式为．
二次项系数化为1得．
配方，得，
．
【点睛】
本题考查了用配方法解一元二次方程的应用，解此题的关键是能正确配方，即加上一次项系数一半的平方．
20．已知关于的一元二次方程有两个不等的实根．
（1）求的取值范围；
（2）当取最大整数值时，的三条边长均满足关于的一元二次方程，求的周长．
【答案】（1）且；（2）的周长为3或9或7．
【解析】
【分析】
（1）根据关于x的一元二次方程，可判断二次项系数不为0；根据方程有两个不相等的实数根，可判断判别式大于0，列出不等式组求解即可．
（2）在此范围内找出最大的整数，解方程，然后分类讨论，求出三角形周长即可．
解：（1）关于的一元二次方程有两个不相等的实数根，
，
解得且．
（2）由（1）得的最大整数值为4；

解得：．
的三条边长均满足关于的一元二次方程，
①三边都为1，则的周长为3；
②三边都为3，则的周长为9；
③三边为1，1，3，因为，不符合题意，舍去；
④三边为1，3，3，则的周长为7．
∴的周长为3或9或7．
【点睛】
本题考查了一元二次方程根的情况与判别式b2-4ac的关系,也考查了构成三角形的条件．解题时注意二次项系数不为0这个隐含条件．
21．如图，在四边形中，对角线、交于点，，，平分，过点作交的延长线于点，连接．
（1）求证：四边形是菱形；
（2）若，，求的长．

【答案】（1）见解析 ；（2）4
【解析】
【分析】
（1）通过角平分线的定义和平行线的性质得出，从而有，则，通过一组对边平行且相等可证明四边形是平行四边形，又因为，所以平行四边形是菱形；
（2）通过菱形的性质可得，，，然后在中利用勾股定理求出OA的长度，然后根据已知得出，再利用直角三角形斜边上的中线等于斜边的一半即可得出答案．
解：（1）∵，
∴．
∵平分，
∴，
∴，
∴．
又∵，
∴．
又∵，
∴四边形是平行四边形．
又∵，
∴□ABCD是菱形．
（2）∵四边形是菱形，对角线、交于点．
∴，，．
∵，
∴．
在中，，，
∴．
∵，
∴．
在中，，为斜边中点，
∴．
【点睛】
本题主要考查平行线的性质，角平分线的性质，菱形的判定及性质，勾股定理，直角三角形斜边中线的性质，掌握平行线的性质，角平分线的性质，菱形的判定及性质，勾股定理，直角三角形斜边中线的性质是解题的关键 ．
22．某宾馆拥有客房100间，经营中发现:每天入住的客房数y（间）与房价x（元）（180≤x≤300）满足一次函数关系，部分对应值如下表：
x（元）
180
260
280
300
y（间）
100
60
50
40

（1）求y与x之间的函数表达式；
（2）已知每间入住的客房，宾馆每日需支出各种费用100元；每间空置的客房，宾馆每日需支出60元，当房价为多少元时，宾馆获得7200元的利润?（宾馆当日利润=当日房费收入-当日支出）
【答案】（1） (180≤x≤300)；（2）260
【解析】
【分析】
（1）设一次函数表达式为，由点的坐标（180，100）、（260，60）利用待定系数法即可求出该一次函数表达式；
（2）设房价为元，依据“宾馆当日利润=当日房费收入-当日支出”列出方程，解方程即可解决问题．
(1)设一次函数的表达式为,
将(180，100)，(260，60)代入得：，
解得：,
∴y与x之间的函数表达式为： (180≤x≤300)．
(2)设房价为x元(180⩽x⩽300)时，依题意得：

即
整理得：
即
解得
180⩽x⩽300

答：当房价为260元时，宾馆当日利润为7200元．
【点睛】
本题考查了一次函数的应用，一元二次方程的应用，理解题意列出方程是解题的关键．
23．我们知道：
；
，
这一种方法称为配方法，利用配方法请解以下各题：
（1）探究：当取不同的实数时，求代数式的最小值．
（2）应用：如图．已知线段，是上的一个动点，设，以为一边作正方形，再以、为一组邻边作长方形．问：当点在上运动时，长方形的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．

【答案】（1）当时，代数式存在最小值为-4；（2）时，长方形的面积存在最大值，最大值为9
【解析】
【分析】
（1）仿照题干，配方后利用非负数的性质确定出结果即可；
（2）设长方形的面积为，根据题意列出S与x的关系式，配方后利用非负数的性质即可得到结果．
解：（1）∵，
∴当时，代数式存在最小值为-4；
（2）设长方形的面积为，
根据题意得：，
则时，存在最大值，最大值为9．
【点睛】
此题考查了配方法的应用，熟练掌握完全平方公式是解本题的关键．
24．如图，在平行四边形ABCD中，，延长DA于点E，使得，连接BE．
求证：四边形AEBC是矩形；
过点E作AB的垂线分别交AB，AC于点F，G，连接CE交AB于点O，连接OG，若，，求的面积．

【答案】（1）见解析；（2）．
【解析】
【分析】
（1）根据平行四边形的性质得到AD∥BC，AD＝BC，推出四边形AEBC是平行四边形，求得∠CAE＝90°，于是得到四边形AEBC是矩形；
（2）根据三角形的内角和得到∠AGF＝60°，∠EAF＝60°，推出△AOE是等边三角形，得到AE＝EO，求得∠GOF＝∠GAF＝30°，根据直角三角形的性质得到OG＝2，根据三角形的面积公式即可得到结论．
解：四边形ABCD是平行四边形，
，，

，
，，
四边形AEBC是平行四边形，
，
，
，
四边形AEBC是矩形；
，
，
，
，，
四边形AEBC是矩形，
，
是等边三角形，
，
，
，
，
，
，
，
，
的面积．
【点睛】
本题考查了矩形的判定和性质，平行四边形的性质，等边三角形的性质，直角三角形的性质，正确的识别图形是解题的关键．
25．（1）如图1，在矩形ABCD中，∠ADC的平分线交BC于点E．交AB的延长线于点F，求证：BE＝BF；
（2）如图2，若G是EF的中点，连接AG、CG、AC，请判断△AGC的形状，并说明理由．
（3）如图3，作∠BED的角平分线EH交AB于点H，已知AB＝9，BH＝2AH，求BC的长．

【答案】（1）见解析；（2）等腰直角三角形，理由见解析；（3）
【解析】
【分析】
（1）由矩形的性质结合角平分线的定义可证得∠ADF＝∠BEF＝∠CDF＝∠F，可证明BE＝BF；
（2）连接BG，由“SAS”可证△AGF≌△CGB，可AG＝CG，进一步可证明∠AGC＝90°，可判定△AGC为等腰直角三角形；
（3）在BH上截取BN＝BE，连接NE，由等腰三角形的性质可求HN＝NE＝BN，可求BN的长，即可求解．
（1）证明：∵四边形ABCD为矩形，
∴AB∥CD，AD∥BC，
∴∠F＝∠CDF，∠ADF＝∠BEF，
∵DF平分∠ADC，
∴∠CDF＝∠ADF，
∴∠F＝∠BEF，
∴BE＝BF；
（2）△AGC为等腰直角三角形，
理由如下：如图，连接BG，

由（1）可知BE＝BF，且∠FBE＝90°，
∴∠F＝45°，
∴∠F＝∠ADF＝45°，
∴AF＝AD＝BC，
∵G为EF中点，
∴BG＝FG，∠EBG＝45°，
在△AGF和△CGB中，
，
∴△AGF≌△CGB（SAS），
∴AG＝CG，∠AGF＝∠BGC，
∴∠BGF+∠AGB＝∠AGB+∠AGC，
∴∠AGC＝∠BGF＝90°，
∴△AGC为等腰直角三角形；
（3）如图，在BH上截取BN＝BE，连接NE，

∵AB＝9，BH＝2AH，
∴AH＝3，BH＝6，
∵∠BEF＝45°，
∴∠BED＝135°，
∵EH平分∠BED，
∴∠BEH＝67.5°，
∴∠BHE＝22.5°，
∵BE＝BN，∠ABC＝90°，
∴∠BEN＝∠BNE＝45°，NE＝BN，
∵∠BNE＝∠BHE+∠HNE＝45°，
∴∠BHE＝∠NEH＝22.5°，
∴HN＝NE＝BN，
∵BH＝BN+NH＝（+1）BN＝6，
∴BN＝6﹣6＝BE，
∴BF＝6﹣6，
∴BC＝AD＝AF＝AB+BF＝9+6﹣6＝6+3．
【点睛】
本题是四边形综合题，考查全等三角形的判定和性质，矩形的性质，等腰直角三角形的性质，在（1）中充分利用矩形的对边分别平行是解题的关键，在（2）构造三角形全等是解题的关键，在（3）中求出BN的长是关键．
26．如图①，已知正方形中，，分别是边，上的点（点，不与端点重合），且，，交于点P，过点作交于点．
   
（1）求证：．
（2）若，试求线段的长．
（3）如图②，连接并延长交于点，若点是的中点，试求的值．
【答案】（1）见解析；（2）；（3）4
【解析】
【分析】
（1）证明△ABE≌△DAF（SAS），得出∠ABE＝∠DAF，得出∠APB＝90°，可得出结论；
（2）根据三角形ABE的面积可求出AP＝，证明△ABP≌△BCH（AAS），由全等三角形的性质得出BH＝AP＝，则PH＝BP﹣BH＝BP﹣AP，可求出答案；
（3）证得∠CBP＝∠CPB，∠QPE＝∠QEP，可得出QE＝QP＝QA，在四边形QABC中，设，，则AB＝BC＝a，AQ＝x，QC＝x+a，由a2+（a﹣x）2＝（x+a）2可得出a，x的关系式，则可求出答案．
（1）证明：∵正方形
∴，
∵
∴
∴
∵
∴
∴
∴
∵
∴
(2) 解：∵，
∴，
，
∴，
∴

∵
∴
∴
∵
∴
∵和，且
∴
∴
∴
（3）解：∵为中点，且
∴为以为底的等腰三角形
∴，
由（1）（2）的证明结果
∵
∴

∴
∴
∵
∴
∴
∴在中，为斜边的中线
∴
由，以及等腰三角形
∴
∴
设，，则在中，
，
根据勾股定理，有
即
得
∴
【点睛】
本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，三角形的面积，平行线的判定，等腰三角形的性质，勾股定理等知识，解题的关键是学会用转化的思想解决问题，学会用方程的思想方法解决问题．