【考点全掌握】人教版数学九年级上册-第二十三章-旋转-单元过关检测02-同步考点（知识清单+例题讲解+课后练习）

这是一份【考点全掌握】人教版数学九年级上册-第二十三章-旋转-单元过关检测02-同步考点（知识清单+例题讲解+课后练习），文件包含第二十三章旋转单元过关检测02解析版docx、第二十三章旋转单元过关检测02原卷版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。

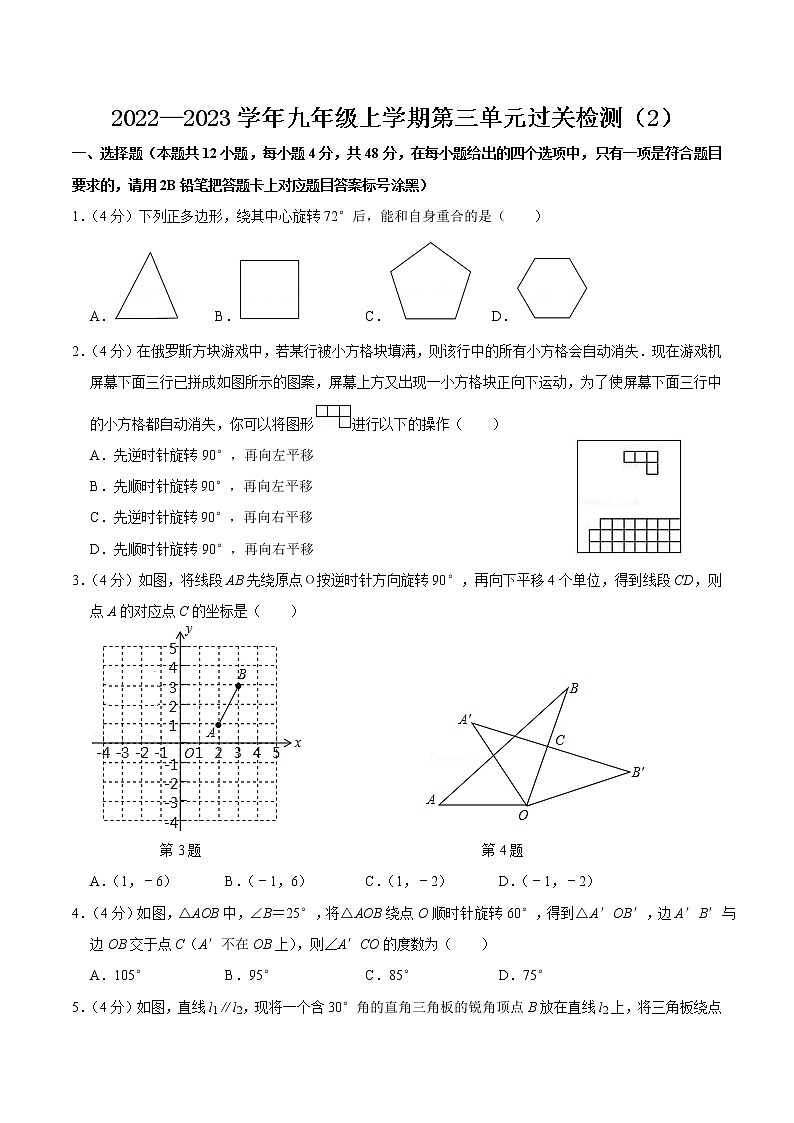
2022—2023学年九年级上学期第三单元过关检测（2）
一、选择题（本题共12小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔把答题卡上对应题目答案标号涂黑）
1．（4分）下列正多边形，绕其中心旋转72°后，能和自身重合的是（　　）
A． B． C． D．
【分析】求出各个选项图形的最小旋转角度，即可做出判断．
【解答】解：A、正三角形的最小旋转角度为120°，故本选项不符合题意；
B、正方形的最小旋转角度90°，故本选项不符合题意；
C、正五边形的最小旋转角度为＝72°，故本选项符合题意；
D、正六边形的最小旋转角度为＝60°，故本选项不符合题意；
故选：C．
2．（4分）在俄罗斯方块游戏中，若某行被小方格块填满，则该行中的所有小方格会自动消失．现在游戏机屏幕下面三行已拼成如图所示的图案，屏幕上方又出现一小方格块正向下运动，为了使屏幕下面三行中的小方格都自动消失，你可以将图形进行以下的操作（　　）
A．先逆时针旋转90°，再向左平移
B．先顺时针旋转90°，再向左平移
C．先逆时针旋转90°，再向右平移
D．先顺时针旋转90°，再向右平移
【分析】根据旋转和平移的性质即可解答．
【解答】解：屏幕上方又出现一小方格块正向下运动，为了使屏幕下面三行中的小方格都自动消失，可以先逆时针旋转90°，再向左平移．
故选：A．
3．（4分）如图，将线段AB先绕原点О按逆时针方向旋转90°，再向下平移4个单位，得到线段CD，则点A的对应点C的坐标是（　　）

A．（1，﹣6） B．（﹣1，6） C．（1，﹣2） D．（﹣1，﹣2）
【分析】先求出A点绕O点逆时针旋转90°后的坐标为（﹣1，2），再求向下平移4个单位后的点的坐标即可．
【解答】解：A点绕O点逆时针旋转90°，得到点A'（﹣1，2），
A'向下平移4个单位，得到C（﹣1，﹣2），
故选：D．

4．（4分）如图，△AOB中，∠B＝25°，将△AOB绕点O顺时针旋转60°，得到△A′OB′，边A′B′与边OB交于点C（A′不在OB上），则∠A′CO的度数为（　　）

A．105° B．95° C．85° D．75°
【分析】由旋转的性质可得∠B＝∠B'＝25°，∠BOB'＝60°，由外角的性质可求解．
【解答】解：∵将△AOB绕点O顺时针旋转60°，得到△A′OB′，
∴∠B＝∠B'＝25°，∠BOB'＝60°，
∴∠A'CO＝∠B'+∠BOB'＝85°，
故选：C．
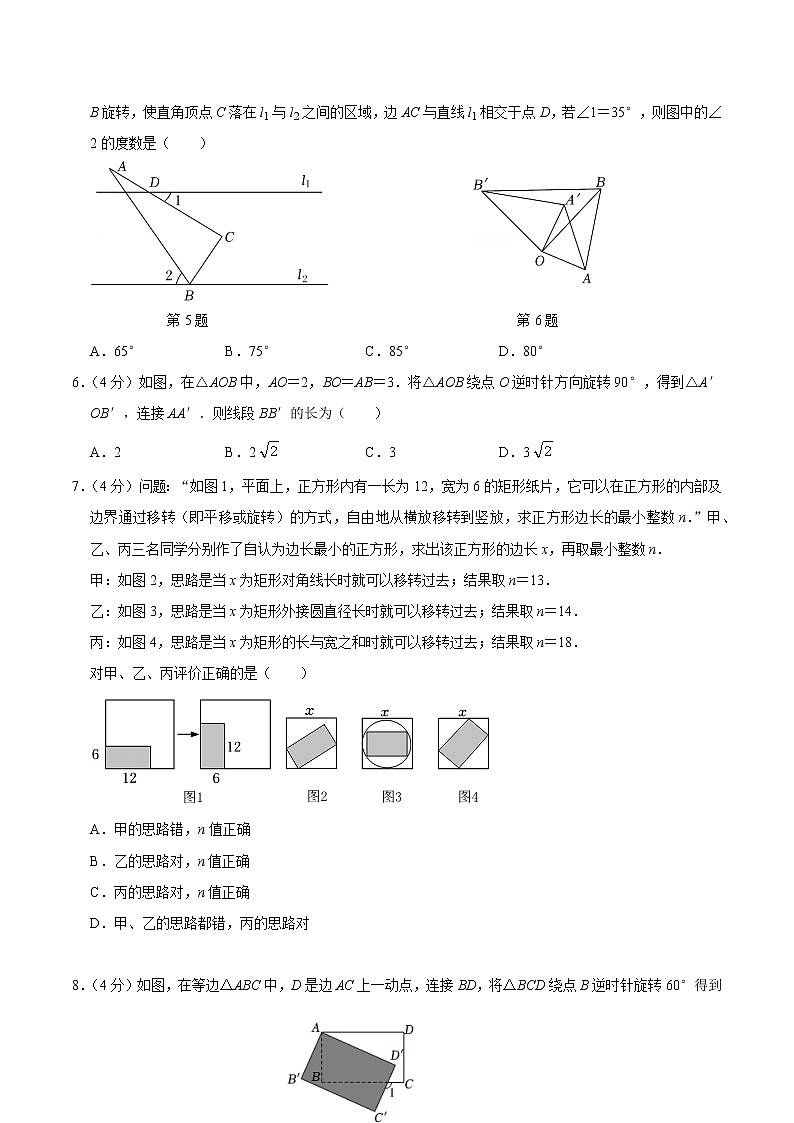
5．（4分）如图，直线l1∥l2，现将一个含30°角的直角三角板的锐角顶点B放在直线l2上，将三角板绕点B旋转，使直角顶点C落在l1与l2之间的区域，边AC与直线l1相交于点D，若∠1＝35°，则图中的∠2的度数是（　　）

A．65° B．75° C．85° D．80°
【分析】过A作CE∥l1，得到CE∥l1∥l2，根据平行线的性质得出∠3，进而求得∠4，再根据平行线的性质可求出答案．
【解答】解：过C作CE∥l1，

∵l1∥l2，
∴CE∥l1∥l2，
∴∠3＝∠1＝35°，
∴∠4＝90°﹣∠3＝55°，
∴∠2＝180°﹣∠4﹣∠ABC＝180°﹣55°﹣60°＝65°．
故选：A．
6．（4分）如图，在△AOB中，AO＝2，BO＝AB＝3．将△AOB绕点O逆时针方向旋转90°，得到△A′OB′，连接AA′．则线段BB′的长为（　　）

A．2 B．2 C．3 D．3
【分析】由旋转的性质可得BO＝B'O＝3，∠BOB'＝90°，由勾股定理可求解．
【解答】解：∵将△AOB绕点O逆时针方向旋转90°，
∴BO＝B'O＝3，∠BOB'＝90°，
∴BB'＝＝＝3，
故选：D．
7．（4分）问题：“如图1，平面上，正方形内有一长为12，宽为6的矩形纸片，它可以在正方形的内部及边界通过移转（即平移或旋转）的方式，自由地从横放移转到竖放，求正方形边长的最小整数n．”甲、乙、丙三名同学分别作了自认为边长最小的正方形，求出该正方形的边长x，再取最小整数n．
甲：如图2，思路是当x为矩形对角线长时就可以移转过去；结果取n＝13．
乙：如图3，思路是当x为矩形外接圆直径长时就可以移转过去；结果取n＝14．
丙：如图4，思路是当x为矩形的长与宽之和时就可以移转过去；结果取n＝18．
对甲、乙、丙评价正确的是（　　）

A．甲的思路错，n值正确
B．乙的思路对，n值正确
C．丙的思路对，n值正确
D．甲、乙的思路都错，丙的思路对
【分析】根据矩形长为12宽为6，可得矩形的对角线长为：，由矩形在该正方形的内部及边界通过平移或旋转的方式，自由地从横放变换到竖放，可得该正方形的边长不小于6，进而可得正方形边长的最小整数n的值．
【解答】解：∵矩形长为12宽为6，
∴矩形的对角线长为：，
∵矩形在该正方形的内部及边界通过平移或旋转的方式，自由地从横放变换到竖放，
∴该正方形的边长不小于6，
∵13＜6＜14，
∴该正方形边长的最小正数n为14．
∴甲的思路正确，长方形对角线最长，只要对角线能通过就可以，但是计算错误，应为n＝14；
乙的思路与计算都正确；
丙的思路与计算都错误；
故选：B．
8．（4分）如图，在等边△ABC中，D是边AC上一动点，连接BD，将△BCD绕点B逆时针旋转60°得到△BAE，连接ED，若BC＝10，则△AED的周长的最小值是（　　）

A．10 B． C． D．20
【分析】由旋转的性质可得BD＝BE，∠DBE＝60°，CD＝AE，可证△DBE是等边三角形，可得BD＝DE＝6，当BD⊥AC时，BD的值最小．由直角三角形的性质可得出答案．
【解答】解：∵将△BCD绕点B逆时针旋转60°得到△BAE，
∴BD＝BE，∠DBE＝60°，CD＝AE，
∴△DBE是等边三角形，
∴BD＝DE＝6，
∴△AED的周长＝AE+AD+DE＝CD+AD+DE＝AC+BD，
∴BD的值最小时，△AED的周长有最小值，
当BD⊥AC时，BD的值最小．
∵∠C＝60°，
∴BD＝5，
∴△AED的周长的最小值是10+5．
故选：C．
9．（4分）如图，将长方形ABCD绕点A顺时针旋转到长方形AB'C'D'的位置，旋转角为α（0°＜α＜90°），若∠1＝120°，则∠α等于（　　）

A．25° B．30° C．45° D．65°
【分析】由旋转的性质可得∠D'＝∠D＝90°，∠DAD'＝α，由四边形内角和定理可求∠BAD'的度数，即可求解．
【解答】解：∵将长方形ABCD绕点A顺时针旋转到长方形AB'CD'的位置，
∴∠D'＝∠D＝90°，∠DAD'＝α，
∵∠BAD'＝360°﹣∠ABC﹣∠D'﹣∠1，
∴∠BAD'＝360°﹣90°﹣90°﹣120°＝60°，
∴∠DAD'＝30°，
故选：B．
10．（4分）如图，点P是等边三角形ABC内一点，且PA＝3，PB＝4，PC＝5，则∠APB的度数是（　　）

A．90° B．100° C．120° D．150°
【分析】根据旋转的性质得BE＝BP＝4，AE＝PC＝5，∠PBE＝60°，则△BPE为等边三角形，得到PE＝PB＝4，∠BPE＝60°，根据勾股定理的逆定理可得到△APE为直角三角形，且∠APE＝90°，即可得到∠APB的度数
【解答】解：∵△ABC为等边三角形，
∴BA＝BC，
如图，将△BPC绕点B逆时针旋转60°得△BEA，连接EP，

∴BE＝BP＝4，AE＝PC＝5，∠PBE＝60°，
∴△BPE为等边三角形，
∴PE＝PB＝4，∠BPE＝60°，
在△AEP中，AE＝5，AP＝3，PE＝4，
∴AE2＝PE2+PA2，
∴△APE为直角三角形，且∠APE＝90°，
∴∠APB＝90°+60°＝150°．
故选：D．
11．（4分）如图Rt△ABC中，∠ACB＝90°，D是斜边AB的中点，将△ABC绕点A按顺时针方向旋转，点C落在CD的延长线上的E处，点B落在F处，若AC＝4，BC＝2，则CE的长为（　　）

A．7.5 B．6 C．6.4 D．6.5
【分析】过点A作AH⊥CE于点H，根据勾股定理可得AB的长，根据直角三角形的性质可得CD的长，根据，可得AH的长，根据勾股定理可得CH的长，根据旋转的性质进一步可得CE的长．
【解答】解：过点A作AH⊥CE于点H，如图所示：

∵∠ACB＝90°，AC＝4，
根据勾股定理，得AB＝10，
∵D是AB的中点，
∴CD＝AB＝5，
∵，
∴，
即，
解得AH＝，
∵AC＝，
根据勾股定理，可得CH＝3.2，
根据旋转的性质，可得AC＝AE，
∴点H是CE的中点，
∴CE＝2CH＝6.4，
故选：C．
12．（4分）如图，在矩形ABCD中，AB＝2，BC＝4，F为BC中点，P是线段BC上一点，设BP＝m（0＜m≤4），连结AP并将它绕点P顺时针旋转90°得到线段PE，连结CE、EF，则在点P从点B向点C的运动过程中，有下面四个结论：①当m≠2时，∠EFP＝135°；②点E到边BC的距离为m；③直线EF一定经过点D；④CE的最小值为．其中结论正确的是（　　）

A．①② B．②③ C．②③④ D．③④
【分析】分两种情况讨论，由“AAS”可证△BAP≌△HPE，△BAP≌△MPE，可得BP＝EH＝m，AB＝PH＝2，EM＝BP＝m，PM＝AB＝2，可得m≠2时，∠EFP＝45°或135°，点E到BC的距离为m，点D在直线EF上，故①错误，②③正确，由等腰直角三角形的性质可求CE的最小值为，故④正确，即可求解．
【解答】解：如图1，当点P在线段BF上时，过点E作EH⊥BC于H，

∵F为BC中点，
∴CF＝BF＝2，
∵将AP绕P顺时针旋转90°得到线段PE，
∴AP＝PE，∠APE＝90°＝∠ABP＝∠PHE，
∴∠BPA+∠EPH＝90°，∠BAP+∠BPA＝90°，
∴∠BAP＝∠EPH，
在△BAP和△HPE中，
，
∴△BAP≌△HPE（AAS），
∴BP＝EH＝m，AB＝PH＝2，
∴FH＝PH﹣PF＝2﹣（2﹣m）＝m，
∴EH＝FH，
∴∠EFH＝45°，
∴∠EFP＝135°，
∵CD＝CF＝2，
∴∠DFC＝45°，
∴点D在直线EF上，
当点P在点F右边时，如图2，

过点E作EM⊥BC，交BC的延长线于点M，
在△BAP和△MPE中，
，
∴△BAP≌△MPE（AAS），
∴EM＝BP＝m，PM＝AB＝2，
∴FM＝FP+PM＝（m﹣2）+2＝m，
∴EM＝FM，
∴∠EFM＝45°，
∵∠DFC＝45°，
∴点D在直线EF上，
综上所述：m≠2时，∠EFP＝45°或135°，点E到BC的距离为m，点D在直线EF上，故①错误，②③正确，
∵点E在DF上运动，
∴当CE⊥DF时，CE有最小值，如图3，

∵CD＝CF，∠DCF＝90°，CE⊥DF，
∴DF＝CD＝2，CE＝DE＝EF＝，
∴CE的最小值为，故④正确，
故选：C．
二、填空题（本题共4个小题，每小题4分，共16分，答题请用黑色墨水笔或签字笔直接答在答题卡相应的位置上）
13．（4分）如图，边长为2的等边△ABO在平面直角坐标系的位置如图所示，点O为坐标原点，点A在x轴上，以点O为旋转中心，将△ABO按顺时针方向旋转120°，得到△OA'B′，则点A′的坐标为 　　．

【分析】首先根据旋转确定OB′在x轴上，然后利用等边三角形的性质与勾股定理即可确定B的坐标．
【解答】解：∵△ABC为等边三角形，
∴∠AOB＝60°，
而以点O为旋转中心，将△ABO按顺时针方向旋转120°，得到△OA'B′，
∴OB′在x轴上，
如图，过A′作A′M⊥OB′于M，
∴∠OA′M＝30°，OM＝MB′，
又OB′＝2，
∴OM＝1，
根据勾股定理得A′M＝，
则点A′的坐标为（1，）．
故答案为：（1，）．

14．（4分）如图，在矩形ABCD中，AC是对角线．将矩形ABCD绕点B顺时针旋转90°到矩形GBEF位置，H是EG的中点．若AB＝6，BC＝8，则线段CH的长为 　 　．

【分析】首先过点H作HM⊥BC于点M，由将ABCD绕点B顺时针旋转90°到GBEF位置，AB＝6，BC＝8，可得BE＝BC＝8，∠CBE＝90°，BG＝AB＝6，又由H是EG的中点，易得HM是△BEG的中位线，继而求得HM与CM的长，由勾股定理即可求得线段CH的长．
【解答】解：过点H作HM⊥BC于点M，
∵将ABCD绕点B顺时针旋转90°到GBEF位置，AB＝6，BC＝8，
∴BE＝BC＝8，∠CBE＝90°，BG＝AB＝6，
∴HM∥BE，
∵H是EG的中点，
∴MH＝BE＝4，BM＝GM＝BG＝3，
∴CM＝BC﹣BM＝8﹣3＝5，
在Rt△CHM中，CH＝＝＝．
故答案为：．

15．（4分）如图，边长为2的等边三角形ABC中，E是对称轴AD上的一个动点，连接CE将线段CE绕点C顺时针旋转60°得到CF，连接DF，则在点E运动过程中，DF的最小值是 　 　．

【分析】取AC的中点G，则CG＝CD，利用SAS证明△CDE≌△CGF，得∠FGC＝∠EDC＝90°，则点F在直线BG上运动，根据垂线段最短从而解决问题．
【解答】解：取AC的中点G，则CG＝CD，

∵将线段CE绕点C顺时针旋转60°得到CF，
∴CE＝CF，∠ECF＝60°，
∵△ABC是等边三角形，
∴∠ACB＝60°，
∴∠DCE＝∠ACF，
∴△CDE≌△CGF（SAS），
∴∠FGC＝∠EDC＝90°，
∴点F在直线BG上运动，
过点D作DH⊥BG，此时DF的最小值即为DH，
∵BD＝BC＝1，
∴DH＝，
故答案为：．
16．（4分）如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，1），（3，0），（2，﹣1）．点M从坐标原点O出发，第一次跳跃到点M1，使得点M1与点O关于点A成中心对称；第二次跳跃到点M2，使得点M2与点M1关于点B成中心对称；第三次跳跃到点M3，使得点M3与点M2关于点C成中心对称；第四次跳跃到点M4，使得点M4与点M3关于点A成中心对称；…，依此方式跳跃，点M2022的坐标是 　 　．

【分析】画出图形，探究规律，利用规律解决问题即可．
【解答】解：如图，由题意，M1（2，2），M2（4，﹣2），M3（0，0），

发现3次应该循环，
∵2022÷3＝674，
∴M2022的坐标与M3的坐标相同，即M2022（0，0）．
故答案为：（0，0）．
三、解答题（本题共8个小题，共86分，答题请用黑色墨水笔或签字笔直接答在答题卡相应的位置上，解答时应写出必要的文字说明、证明步骤或演算步骤.）
17．（8分）如图，在边长为1的正方形组成的网格中建立直角坐标系，△AOB的顶点均在格点上，点O为原点，点A、B的坐标分别是A（3，2）、B（1，3）．
（1）将△AOB向下平移4个单位，则点B的对应点坐标为 　 　；
（2）将△AOB绕点O逆时针旋转90°后得到△A1OB1，请在图中作出△A1OB1；
（3）求△A1OB1的面积．

【分析】（1）利用平移变换的性质作出图形，可得结论；
（2）利用旋转变换的性质作出图形即可；
（3）把三角形的面积看成矩形的面积减去周围的三个三角形面积即可．
【解答】解：（1）如图，△A′B′C′即为所求，B′（1，﹣1）．
故答案为：（1，﹣1）；
（2）如图，△A1OB1即为所求；
（3）△A1OB1的面积＝3×3﹣×1×2﹣×2×3﹣×1×3＝3.5．

18．（8分）如图，将等边△ABC绕点C顺时针旋转60°，得到△ADC，分别过点A、点C作BC、AD边上的高，交BC、AD于点E、F．
（1）求证：四边形AECF是矩形；
（2）连接BD，若AB＝3，求BD的长．

【分析】（1）根据等边三角形的性质得到AB＝AC＝BC，∠ACB＝60°，根据旋转的性质得到AC＝CD，∠ACD＝60°，得到△ACD是等边三角形，得到∠DAC＝60°，根据平行四边形的性质得到EA⊥AD，根据矩形的判定定理即可得到结论；
（2）连接BD交AC于O，由（1）知，△ACD是等边三角形，推出四边形ABCD是菱形，得到AC⊥BD，∠ABO＝∠ABC＝30°，根据勾股定理即可得到结论．
【解答】（1）证明：∵△ABC是等边三角形，
∴AB＝AC＝BC，∠ACB＝60°，
∵将等边△ABC绕点C顺时针旋转60°，得到△ADC，
∴AC＝CD，∠ACD＝60°，
∴△ACD是等边三角形，
∴∠DAC＝60°，
∴∠DAC＝∠ACB，
∴AD∥BC，
∵AE⊥BC，CF⊥AD，
∴EA⊥AD，
∴∠AEC＝∠EAF＝∠AFC＝90°，
∴四边形AECF是矩形；
（2）解：连接BD交AC于O，
由（1）知，△ACD是等边三角形，
∴AD＝CD＝AC＝AB＝BC，
∴四边形ABCD是菱形，
∴AC⊥BD，∠ABO＝∠ABC＝30°，
∴AO＝AB＝，
∴BD＝2BO＝2×＝3．

19．（10分）如图，已知Rt△ABC中，∠ACB＝90°，先把△ABC绕点C顺时针旋转90°至△EDC后，再把△ABC沿射线BC平移至△GFE，DE、FG相交于点H．
（1）判断线段DE、FG的位置关系，并说明理由；
（2）连结AG，求证：四边形ACEG是正方形．

【分析】（1）由旋转和平移的性质可得∠BAC＝∠CED，∠ABC＝∠GFE，由余角的性质可得结论；
（2）由旋转和平移的性质可得AC＝GE，AC∥GE，AC＝CE，∠ACE＝90°，可得结论．
【解答】（1）解：DE⊥FG，理由如下：
∵把△ABC绕点C顺时针旋转90°至△EDC，
∴∠BAC＝∠CED，
∵把△ABC沿射线BC平移至△GFE，
∴∠ABC＝∠GFE，
∵∠BAC+∠ABC＝90°，
∴∠CED+∠GFE＝90°，
∴∠FHE＝90°，
∴DE⊥GF；
（2）∵把△ABC沿射线BC平移至△GFE，
∴AC＝GE，AC∥GE，
∴四边形ACEG是平行四边形，
∵把△ABC绕点C顺时针旋转90°至△EDC，
∴AC＝CE，∠ACE＝90°，
∴四边形ACEG是正方形．
20．（10分）如图，△ABC与△ACD为正三角形，点O为射线CA上的动点，作射线OM与射线BC相交于点E，将射线OM绕点O逆时针旋转60°，得到射线ON，射线ON与射线CD相交于点F．
（1）如图1，点O与点A重合时，点E，F分别在线段BC，CD上，求证：△AEC≌△AFD；
（2）如图2，当点O在CA的延长线上时，E，F分别在线段BC的延长线和线段CD的延长线上，请写出CE、CF、CO三条线段之间的数量关系，并说明理由．

【分析】（1）利用SAS证明△AEC≌△AFD即可得出结论；
（2）过点O作OH∥BC，交CF于H，可知△COH是等边三角形，再利用ASA证明△OHF≌△OCE，从而解决问题．
【解答】（1）证明：∵△ABC与△ACD为正三角形，
∴AB＝AC＝BC＝AD＝CD，∠BAC＝∠BCA＝∠ADC＝∠DAC＝60°，
∵将射线OM绕点O逆时针旋转60°，
∴AE＝AF，∠EAF＝60°，
∴∠BAC＝∠CAD＝∠EAF＝60°，
∴∠EAC＝∠DAF，且AC＝AD，AE＝AF，
在△AEC与△AFD中，
，
∴△AEC≌△AFD（SAS），
（2）解：CE+CO＝CF，
理由：如图，过点O作OH∥BC，交CF于H，

∴∠HOC＝∠BCA＝60°，∠OHC＝∠HCE＝60°，
∴△COH是等边三角形，
∴OC＝CH＝OH，
∵∠EOF＝∠COH＝∠CHO＝∠BCA＝60°，
∴∠COE＝∠FOH，∠OCE＝∠OHF＝120°，OH＝OC，
在△OHF与△OCE中，
，
∴△OHF≌△OCE（ASA），
∴CE＝FH，
∵CF＝CH+FH，
∴CF＝CO+CE．
21．（12分）如图所示，点P的坐标为（1，3），把点P绕坐标原点O逆时针旋转90°后得到点Q．
（1）写出点Q的坐标是　 　；
（2）若把点Q向右平移a个单位长度，向下平移a个单位长度后，得到的点M（m，n）落在第四象限，求a的取值范围；
（3）在（2）条件下，当a取何值，代数式m2+2n+5取得最小值．

【分析】（1）根据旋转变换的性质即可解决问题．
（2）根据不等式组即可解决问题．
（3）利用配方法解决问题即可．
【解答】解：（1）由题意：Q（﹣3，1）．
故答案为（﹣3，1）．

（2）把点Q（﹣3，1）向右平移a个单位长度，向下平移a个单位长度后，
得到的点M的坐标为（﹣3+a，1﹣a），而M在第四象限，则有，
解得a＞3，
即a的范围为a＞3．
（3）由（2）得，m＝﹣3+a，n＝1﹣a
∴m2+2n+5＝（a﹣3）2+2（1﹣a）+5
＝a2﹣6a+9+2﹣2a+5
＝a2﹣8a+16
＝（a﹣4）2
∵（a﹣4）2≥0，
∴当a＝4时，代数式m2+2n+5的最小值为0．
22．（12分）如图，平行四边形ABCD中，AB⊥AC，AB＝1，BC＝．对角线AC，BD
相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．
（1）证明：当旋转角为90°时，四边形ABEF是平行四边形；
（2）证明：在旋转过程中，线段AF与EC总保持相等；
（3）在旋转过程中，当AC绕点O顺时针旋转多少度时，四边形BEDF是菱形，请给出证明．

【分析】（1）根据平行四边形的判定定理证明．
（2）通过三角形全等证明．
（3）根据菱形的性质和判定求解．
【解答】（1）证明：如图：

∵平行四边形ABCD中，AD∥BC，
∴AF∥BE，
∵旋转角为90°时，∠AOF＝90°，
∵AB⊥AC，
∴∠BAC＝90°，
∴∠BAC＝∠AOF，
∴AB∥EF，
∴四边形ABEF是平行四边形．
（2）证明：∵四边形ABCD是平行四边形，
∴OA＝OC，AD∥BC，
∴∠OAF＝∠OCE，
∵∠AOF＝∠COE，
∴△AOF≌△COE（ASA）．
∴AF＝CE．
∴在旋转过程中，线段AF与EC总保持相等．
（3）当AC绕点O顺时针旋转45度时，四边形BEDF是菱形．
理由如下：
由（2）知：AF＝CE，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴DF＝BE，DF∥BE，
∴四边形BEDF是平行四边形．
如图：

∵AB⊥AC，AB＝1，BC＝，
∴AC＝＝2，
∵四边形ABCD是平行四边形，
∴AO＝AC＝1，
∴AO＝AB，
∵AB⊥AC，
∴∠AOB＝45°
∵AC绕点O顺时针旋转45度，
∴∠AOF＝45°，
∴∠BOF＝90°，
∴EF⊥BD．
∴四边形BEDF是菱形．
23．（12分）如图，已知正方形ABCD的面积为S．
（1）求作：四边形A1B1C1D1，使得点A1和点A关于点B对称，点B1和点B关于点C对称，点C1和点C关于点D对称，点D1和点D关于点A对称；（只要求画出图形，不要求写作法）
（2）用S表示（1）中作出的四边形A1B1C1D1的面积S1；
（3）若将已知条件中的正方形改为任意四边形，面积仍为S，并按（1）的要求作出一个新的四个边形，面积为S2，则S1与S2是否相等，为什么？

【分析】（1）根据对称的性质可知．使得点A1和点A关于点B对称，即是连接AB并延长相同的长度找到对应点A′，其它三点同样的方法找到对应点，顺次连接．
（2）设正方形ABCD的边长为a，根据两个正方形边长的比值，利用面积比等于相似比，来求小正方形的面积．
（3）相等．因为一个四边形可以分成两个三角形，根据三角形的面积公式，等底等高的三角形面积相等．
【解答】解：（1）如图①所示．
（2）设正方形ABCD的边长为a，
则AA1＝2a，S△AA1D1＝•AA1•AD1＝a2，
同理，S△BB1A1＝S△CC1B1＝S△DD1C1＝a2，
∴S1＝S△AA1D1+S△BB1A1+S△CC1B1+S△DD1C1+S正方形ABCD＝5a2＝5S．
（本问也可以先证明四边形A1B1C1D1是正方形，再求出其边长为a，从而算出S四边形A1B1C1D1＝5S）
（3）S1＝S2
理由如下：
首先画出图形②，连接BD、BD1，
∵△BDD1中，AB是中线，
∴S△ABD1＝S△ABD．
又∵△AA1D1中，BD1是中线，
∴S△ABD1＝S△A1BD1
∴S△AA1D1＝2S△ABD
同理，得S△CC1B1＝2S△CBD
∴S△AA1D1+S△CC1B1＝2（S△ABD+S△CBD）＝2S．
同理，得S△BA1B1+S△DD1C1＝2S，
∴S2＝S△AA1D1+S△BB1A1+S△CC1B1+S△DD1C1+S四边形ABCD＝5S．
由（2）得，S1＝5S．
∴S1＝S2．
24．（14分）如图，有一副直角三角板如图1放置（其中∠D＝45°，∠C＝30°），PA，PB与直线MN重合，且三角板PAC，三角板PBD均可以绕点P逆时针旋转．
（1）在图1中，∠DPC＝　 　；
（2）①如图2，若三角板PBD保持不动，三角板PAC绕点P逆时针旋转，转速为10°/秒，转动一周三角板PAC就停止转动，在旋转的过程中，当旋转时间为多少时，有PC∥DB成立；
②如图3，在图1基础上，若三角板PAC的边PA从PN处开始绕点P逆时针旋转，转速为3°/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速为2°/秒，当PC转到与PA重合时，两三角板都停止转动，在旋转过程中，当∠CPD＝∠BPM时，求旋转的时间是多少？


【分析】（1）根据平角的定义即可得到结论；
（2）①如图1，根据平行线的性质得到∠CPN＝∠DBP＝90°，求得∠APN＝30°，于是得到结论；如图2，根据平行线的性质得到∠CPB＝∠DBP＝90°，根据三角形的内角和得到∠CPA＝60°，求得∠APM＝30°，于是得到结论；
②设旋转的时间为t秒，由题知，∠APN＝3t°，∠BPM＝2t°，根据周角的定义得到∠CPD＝360°﹣∠BPD﹣∠BPN﹣∠APN﹣∠APC＝360°﹣45°﹣（180°﹣2t°）﹣（3t°）﹣60°＝75°﹣t°，列方程即可得到结论．
【解答】解：（1）∵∠BPD＝∠D＝45°，∠APC＝60°，
∴∠DPC＝180°﹣45°﹣60°＝75°，
故答案为：75°；
（2）①如图1，此时，BD∥PC成立，
∵PC∥BD，∠DBP＝90°，
∴∠CPN＝∠DBP＝90°，
∵∠C＝30°，
∴∠CPA＝60°，
∴∠APN＝30°，
∵转速为10°/秒，
∴旋转时间为3秒；
如图2，PC∥BD，
∵PC∥BD，∠PBD＝90°，
∴∠CPB＝∠DBP＝90°，
∵∠C＝30°，
∴∠CPA＝60°，
∴∠APM＝30°，
∵三角板PAC绕点P逆时针旋转D的角度为180°+30°＝210°，
∵转速为10°/秒，
∴旋转时间为21秒，
综上所述，当旋转时间为3或21秒时，PC∥DB成立；
②设旋转的时间为t秒，由题知，∠APN＝3t°，∠BPM＝2t°，
∴∠BPN＝180°﹣∠BPM＝180°﹣2t°，
∴∠CPD＝360°﹣∠BPD﹣∠BPN﹣∠APN﹣∠APC＝360°﹣45°﹣（180°﹣2t°）﹣（3t°）﹣60°＝75°﹣t°，
当∠CPD＝∠BPM，即2t°＝75°﹣t°，
解得：t＝25，
∴当∠CPD＝∠BPM，求旋转的时间是25秒．