初中数学华师大版八年级上册第13章 全等三角形13.3 等腰三角形2 等腰三角形的判定课堂教学ppt课件

这是一份初中数学华师大版八年级上册第13章 全等三角形13.3 等腰三角形2 等腰三角形的判定课堂教学ppt课件，共30页。PPT课件主要包含了学习目标，本节要点，学习流程，知识点，等腰三角形的判定，感悟新知，等边三角形的判定，本节小结，有一个角等于60°，等角对等边等内容，欢迎下载使用。

等腰三角形的判定等边三角形的判定
1. 判定定理 如果一个三角形有两个角相等，那么这两个角所对的边也相等(简写成“等角对等边”).几何语言：如图13.3-18，在△ ABC 中，∵∠ B= ∠ C，∴ AB=AC.
2. 等腰三角形的性质与判定的异同相同点：使用的前提都是“在同一个三角形中”.不同点：性质：两边相等→这两边所对的角相等.判定：两角相等→这两角所对的边相等.
特别提醒等腰三角形的定义也是一种判定方法，判定定理就是转化为定义再判断，也是证明在同一个三角形中两条线段相等的方法.
如图13.3-19，在△ ABC 中，P 是BC 边上一点，过点P 作BC 的垂线，交AB 于点Q，交CA 的延长线于点R，若AQ=AR，则△ ABC 是等腰三角形吗？请说明理由.
解题秘方：利用“等角对等边”判定等腰三角形，只需证明三角形两个内角相等即可.
解：△ ABC 是等腰三角形. 理由如下：∵ AQ=AR，∴∠ R= ∠ AQR.又∵∠ BQP= ∠ AQR，∴∠ R= ∠ BQP.∵ RP ⊥ BC，∴∠ RPB= ∠ RPC=90°.∴∠ B+ ∠ BQP=90°，∠ C+ ∠ R=90°，∴∠ B= ∠ C. ∴ AB=AC.∴△ ABC 是等腰三角形.
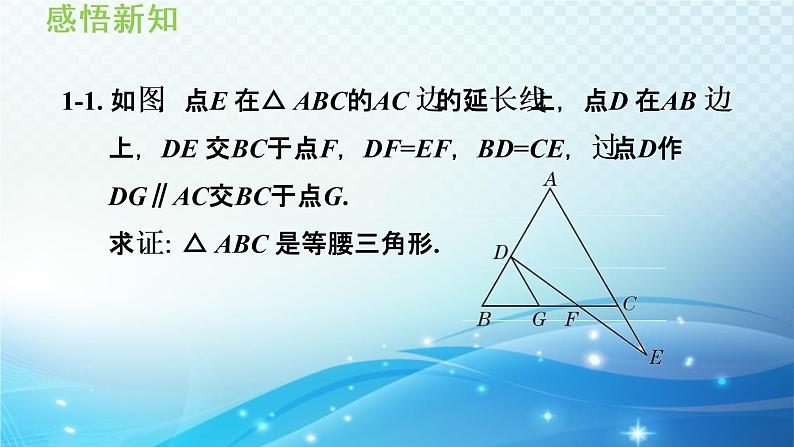
1-1. 如图，点E 在△ ABC的AC 边的延长线上，点D 在AB 边上，DE 交BC于点F，DF=EF，BD=CE，过点D作DG∥AC交BC于点G.求证：△ ABC 是等腰三角形.
证明：∵DG∥AC，∴∠DGB＝∠ACB，∠DGF＝∠ECF. 又∵∠DFG＝∠EFC，DF＝EF， ∴△GDF≌△CEF()．∴DG＝EC. ∵BD＝CE，∴BD＝DG.∴∠DGB＝∠B.∵∠DGB＝∠ACB，∴∠B＝∠ACB. ∴AC＝AB，即△ABC是等腰三角形．
1. 判定定理1 三个角都相等的三角形是等边三角形.几何语言：如图13.3-20，在△ ABC 中，∵∠ A= ∠ B= ∠ C，∴△ ABC 是等边三角形.
2. 判定定理2 有一个角等于60°的等腰三角形是等边三角形.几何语言：如图13.3-20，在△ ABC 中，∵ AB=AC， ∠ A=60 °(或∠ B=60 °或∠ C=60°)，∴△ ABC 是等边三角形.
3. 证明等边三角形的思维导图
特别解读1. 在等腰三角形中，只要有一个角是60°，无论这个角是顶角还是底角，判定定理2 都成立.2. 等边三角形的判定方法：(1)若已知三边关系，一般选用定义判定；(2)若已知三角关系，一般选用判定定理1 判定；(3)若已知该三角形是等腰三角形，一般选用判定定理2 判定.
如图13.3-21，在等边三角形ABC 中，∠ ABC 和∠ ACB 的平分线相交于点O，OB，OC 的垂直平分线分别交BC 于点E，F，连结OE，OF. 求证：△ OEF 是等边三角形.
解题秘方：利用等边三角形的判定定理1，通过求∠ OEF=∠ OFE= ∠EOF=60°，得△ OEF 是等边三角形.
证明：∵△ ABC 是等边三角形，∴∠ ABC= ∠ ACB=60°.∵ CO，BO 分别平分∠ ACB，∠ ABC，∴∠ OBE= ∠ OCF=30°.由OB、OC 的垂直平分线分别交BC 于点E，F，易证△ OGE ≌△ BGE，△ OHF ≌△ CHF，∴ OE=BE，OF=CF.
∴∠ BOE= ∠ OBE=30°，∠ COF= ∠ OCF=30°.∴ ∠ OEF= ∠ BOE+ ∠ OBE=60 °， ∠ OFE= ∠ COF+∠ OCF=60°.∴∠ OEF= ∠ OFE=60°. ∴∠ EOF=60°.∴△ OEF 是等边三角形.
教你一招：1. 从角的角度证明三角形是等边三角形，一是证明三角形的三个内角相等；二是求出三角形的三个内角度数都是60°.2. 在已知的等边三角形内部判定某个三角形是等边三角形，原等边三角形的三个内角为60°，为求新三角形的内角度数提供了条件.
2-1. 如图， △ ABC 是等边三角形，点E，F，G 分别在AB，BC，CA上， 且AE=BF=CG.求证：△ EFG 是等边三角形.
证明：∵△ABC是等边三角形，∴AB＝BC＝AC，∠A＝∠B＝∠C＝60°.∵AE＝BF＝CG，∴AB－AE＝BC－BF＝AC－CG，即BE＝CF＝AG.∴△AEG≌△BFE≌△CGF()．∴EG＝EF＝FG.∴△EFG是等边三角形．
2-2. 如图， △ ABC为等边三角形， ∠ 1=∠ 2= ∠ 3. 求证：△ DEF 是等边三角形.
证明：∵△ABC是等边三角形，∴∠BAC＝∠ABC，AB＝AC.∵∠1＝∠2，∴∠BAC－∠1＝∠ABC－∠2，即∠CAF＝∠ABD.
如图13.3-22，点C 为线段AB 上一点，△ ACM，△ CBN 都是等边三角形，AN，MC 相交于点E，BM、CN 相交于点F，连结EF. 求证：(1)AN=BM；(2)△CEF 是等边三角形.
解题秘方：(1)要证AN=BM，只需证△ ACN ≌△ MCB；(2)根据已知条件，易求∠ ECF=60°，故证明△ ECF为等腰三角形即可.
证明：(1)∵△ ACM，△ CBN 都是等边三角形，∴ AC=CM，CN=BC，∠ ACM= ∠ BCN=60°.∴∠ ACM+ ∠ MCN= ∠ BCN+ ∠ MCN，即∠ ACN= ∠ MCB.在△ ACN 和△ MCB 中，∴△ ACN ≌△ MCB(). ∴ AN=BM.
(2)∵△ ACN ≌△ MCB，∴∠ ENC= ∠ FBC.∵∠ ECN=180°－∠ ACM－∠ NCB=60°，∴∠ ECN= ∠ FCB.在△ ECN 和△ FCB 中，∴△ ECN ≌△ FCB().∴ CE=CF.又∵∠ ECF=60°，∴△ CEF 是等边三角形.
3-1. 如图， △ ABC 为等边三角形，D 为BC边上的一点. 在△ ABC的外角的平分线CE 上取点E，使CE=BD，连结AD，AE，DE. 请判断△ ADE 的形状，并说明理由.
又∵BD＝CE，∴△ABD≌△ACE()．∴AD＝AE，∠BAD＝∠CAE.∵∠DAE＝∠DAC＋∠CAE＝∠DAC＋∠BAD＝∠BAC＝60°，∴△ADE是等边三角形．