第8节：椭圆的标准方程和性质(1)学案-江苏省对口高考数学一轮复习

这是一份第8节：椭圆的标准方程和性质(1)学案-江苏省对口高考数学一轮复习，共4页。学案主要包含了学习目标，课前知识整理，自主复习单，考点探析单，方法点拨，能力提升单等内容，欢迎下载使用。
1. 理解椭圆的两个定义和两种不同类型的标准方程.
2. 会根据已知条件确定椭圆的方程.
3. 理解椭圆的标准方程及焦点.离心率.准线等参数之间的联系，能根据相关条件求各类参数.
【课前知识整理】
1.椭圆的定义：
（1）第一定义 ：平面内到两个定点的距离之和等于________________的点的轨迹称为椭圆，两个定点称为________，两个焦点之间的距离称为椭圆的_______.
说明：，点的轨迹表示线段，不能形成图形
（2）第二定义：椭圆是平面上到定点的距离与到相应定直线的距离之比等于_____________的点的轨迹，定点为椭圆的 ，定直线为椭圆的 .
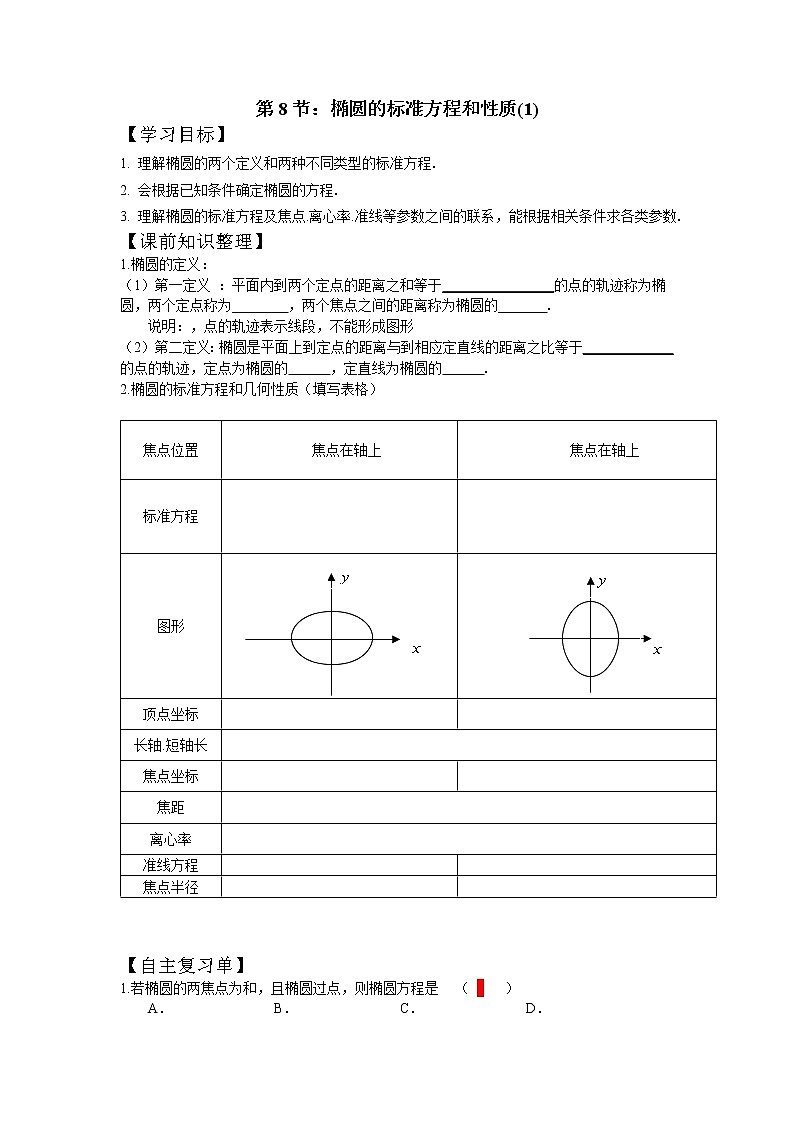
2.椭圆的标准方程和几何性质（填写表格）
【自主复习单】
1.若椭圆的两焦点为和，且椭圆过点，则椭圆方程是（ ）
A．B．C．D．
(本题知识点：_________________)
2.椭圆和具有（ ）
A．相同的离心率 B．相同的焦点 C．相同的顶点 D．相同的长短轴
(本题知识点：____________________)
3. 已知椭圆的标准方程为，其长轴长为 ，短轴长为 ，焦点坐标为__________，离心率为_____，准线方程为__________，两准线之间的距离为_____
4. 若椭圆两准线间的距离等于焦距的倍，则这个椭圆的离心率为 .
5．已知是椭圆上的一点，若到椭圆右准线的距离是，则点到左焦点的距离是 .
【考点探析单】
活动一：利用椭圆的定义解题．
1. 设椭圆的焦点为，直线过点，且与椭圆相交于两点，求的周长.
2. 如果椭圆上的一点到左焦点的距离为，求点到右准线的距离和点的横坐标.
【分析】的周长即点到两个焦点和点到两个焦点的距离之和，可由第一定义解出.
【解】1.由题意可知, ,
=又即的周长等于.
【方法点拨】题目中若涉及到焦点，准线的问题要注意利用椭圆的定义，另外要善于运用数型结合的数学思想来指导解题.
【解】2
活动二：求椭圆的标准方程.
1. 两个焦点的坐标分别是并且椭圆经过点.
2. 两个焦点的坐标分别是椭圆上一点P到两焦点距离之和等于10.
3. 椭圆过点求椭圆的标准方程.
【分析】可先由两点间的距离公式求出到两个焦点间的距离.
【解】因为椭圆的焦点在y轴上，所以设它的标准方程为.
由椭圆的定义知：
∴，又
∴，所以椭圆方程为.
【方法点拨】确定椭圆的标准方程一般用待定系数法设出椭圆的方程，只要求出三个参数中的两个，并确定焦点位置就可以了.
【解】2.
3.
.
活动三：利用椭圆的几何性质解决相关问题.
1. 椭圆的一个焦点是求.
2. 求椭圆的长轴和短轴长，离心率，焦点和顶点坐标及准线方程.
【分析】化为标准方程后把焦点坐标表示成的关系式.
【解】将椭圆方程化成标准方程，即，椭圆一个焦点为
∴ ∴，即.
【方法点拨】椭圆的两个标准方程中，如果的分母大，焦点就在轴上，如果的分母大，焦点就在轴上.
【解】2.
【能力提升单】
1. 设一动点到直线的距离与它到点的距离之比为，则动点的轨迹方程是（ ）
A. B. C. D.
2. 椭圆的两个焦点和短轴两个顶点，是一个含角的菱形的四个顶点，则椭圆的离心率为 ( )
A. B. C. D.或
3. 已知椭圆的长轴长是短轴长的倍，长.短轴都在坐标轴上，过点，则椭圆的方程是___________________.
4. 椭圆的准线平行于轴，则的取值范围_________________.
5. 若表示焦点在轴上的椭圆，求实数的范围.
焦点位置
焦点在轴上
焦点在轴上
标准方程
图形
顶点坐标
长轴.短轴长
焦点坐标
焦距
离心率
准线方程
焦点半径