数学九年级下册第五章 圆综合与测试课后练习题

一、选择题(每小题3分,共36分)

1.(2021于都期末)如图所示,AB是☉O的直径,C为圆内一点,则下列说法中正确的是(　B　)

第1题图

A.AC是☉O的弦 B.∠BOC是圆心角 

C.∠C是圆周角 D.AC+OC<AB

2.下列图形中,∠1一定小于∠2的是(　B　)

A          B          C          D

3.(2021金山一模)已知在矩形ABCD中,AB=5,对角线AC=13,☉C的半径长为12,下列说法正确的是(　D　)

A.☉C与直线AB相交 B.☉C与直线AD相切

C.点A在☉C上   D.点D在☉C内

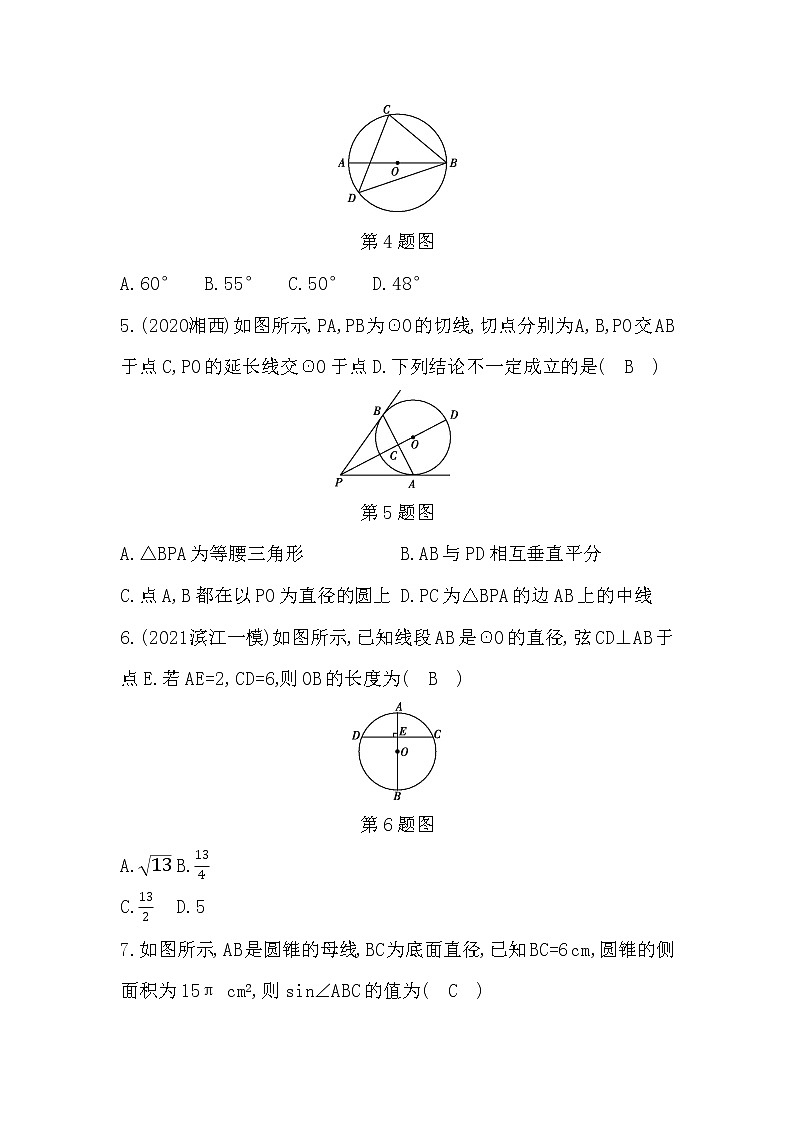
4.(2021金坛模拟)如图所示,AB是☉O的直径,C,D是☉O上两点,若∠ABC=40°,则∠BDC的度数是(　C　)

第4题图

A.60° B.55° C.50° D.48°

5.(2020湘西)如图所示,PA,PB为☉O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交☉O于点D.下列结论不一定成立的是(　B　)

第5题图

A.△BPA为等腰三角形    B.AB与PD相互垂直平分

C.点A,B都在以PO为直径的圆上 D.PC为△BPA的边AB上的中线

6.(2021滨江一模)如图所示,已知线段AB是☉O的直径,弦CD⊥AB于点E.若AE=2,CD=6,则OB的长度为(　B　)

第6题图

A. B. 

C. D.5

7.如图所示,AB是圆锥的母线,BC为底面直径,已知BC=6 cm,圆锥的侧面积为15π cm2,则sin∠ABC的值为(　C　)

第7题图

A. B. C. D.

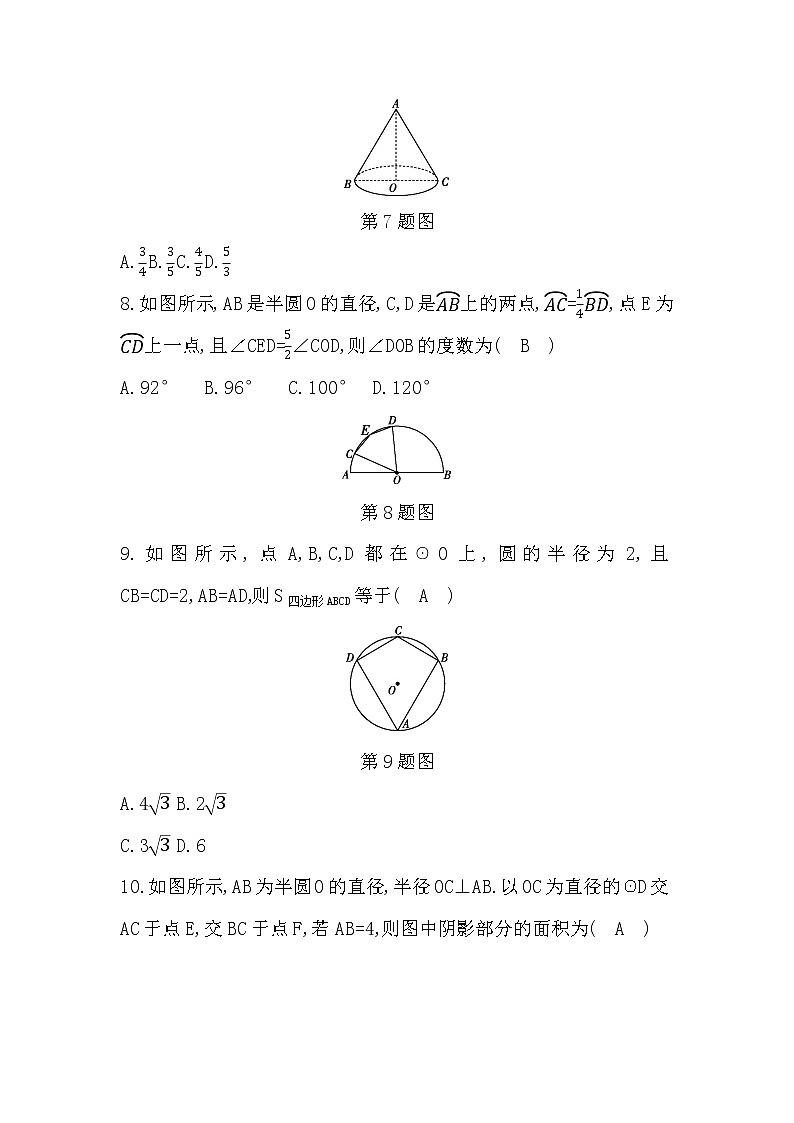
8.如图所示,AB是半圆O的直径,C,D是上的两点,=,点E为上一点,且∠CED=∠COD,则∠DOB的度数为(　B　)

A.92° B.96° C.100° D.120°

第8题图

9.如图所示,点A,B,C,D都在☉O上,圆的半径为2,且CB=CD=2,AB=AD,则S四边形ABCD等于(　A　)

第9题图

A.4 B.2

C.3 D.6

10.如图所示,AB为半圆O的直径,半径OC⊥AB.以OC为直径的☉D交AC于点E,交BC于点F,若AB=4,则图中阴影部分的面积为(　A　)

第10题图

A.2π-2 B.4π-2

C.4π-4 D.π-2

11.(2021高青一模)如图所示,圆心为M的量角器的直径的两个端点A,B分别在x轴正半轴、y轴正半轴上(包括原点O),AB=4.点P,Q分别在量角器60°,120°刻度线外端,连接MP.量角器从点A与点O重合滑动至点Q与点O重合的过程中,线段MP扫过的面积为(　D　)

第11题图

A.π+  B.π

C.3   D.π+2

12.如图所示,AB是☉O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足=,连接AF并延长交☉O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan E=;④S△DAF=6.其中正确的有(　A　)

第12题图

A.1个 B.2个

C.3个 D.4个

二、填空题(每小题3分,共18分)

13.(2021诸暨期末)如图所示,已知☉O上三点A,B,C,切线PA交OC延长线于点P,若OP=2OC,则 ∠ABC=　30°　. 

第13题图

14.(2020益阳)小明家有一个如图所示的闹钟,他观察发现圆心角   ∠AOB=90°,测得的长为36 cm,则的长为　12　cm. 

第14题图

15.如图所示,八边形ABCDEFGH是正八边形,其外接圆的半径为,则正八边形的面积为　4　. 

第15题图

16.如图所示,☉O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则☉O的面积为　4π　. 

第16题图

17.(2020鸡西)在半径为的☉O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP=　或或　. 

18.如图所示,已知AB=AC=BE=CD,AD=AE,点F为△ADE的外心,若    ∠DAE=40°,则∠BFC=　140　°. 

第18题图

三、解答题(共46分)

19.(6分)(2021武汉模拟)如图所示,在☉O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.

证明:∵AB=CD,∴=.

∴-=-,即=.

∴∠C=∠B.∴CE=BE.

20.(6分)如图所示,已知等边三角形ABC内接于☉O,AD是☉O的内接正十二边形的一条边,连接CD,若CD=6 cm,求☉O的半径.

解:如图所示,连接OA,OD,OC.

∵等边三角形ABC内接于☉O,AD为内接正十二边形的一边,

∴∠AOC=×360°=120°,∠AOD=×360°=30°,

∴∠COD=∠AOC-∠AOD=90°.∵OC=OD,∴△OCD是等腰直角三角形,

∴OC=OD=CD=×6=6,即☉O的半径为6 cm.

21.(10分)如图所示,已知AB是☉O的直径,CD与☉O相切于点C,过点B作BE⊥DC,交DC延长线于点E.

(1)求证:BC是∠ABE的平分线;

(2)若DC=8,☉O的半径OA=6,求CE的长.

(1)证明:∵CD与☉O相切于点C,∴OC⊥DC.

∵BE⊥DC,∴BE∥OC,∴∠EBC=∠OCB.

∵OC=OB,∴∠OCB=∠OBC,∴∠EBC=∠OBC,即BC是∠ABE的平分线.

(2)解:如图所示,过点C作CM⊥BD于点M,∵BC是∠ABE的平分线,   BE⊥CE,∴CE=CM.

∵OC⊥DC,∴∠OCD=90°.

∵DC=8,OC=OA=6,∴OD===10.

∵S△DCO=×CD×OC=×OD×CM,

∴8×6=10×CM,解得CM=4.8,即CE=CM=4.8.

22.(12分)如图所示,在△ABC中,AB=AC,以AB为直径的☉O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.

(1)求证:直线DF是☉O的切线;

(2)求证:BC2=4CF·AC;

(3)若☉O的半径为4,∠CDF=15°,求阴影部分的面积.

(1)证明:如图所示,连接OD,∵AB=AC,∴∠ABC=∠C.

而OB=OD,∴∠ODB=∠ABC=∠C.

∵DF⊥AC,∴∠CDF+∠C=90°.∴∠CDF+∠ODB=90°.

∴∠ODF=90°.∵OD为☉O的半径,∴直线DF是☉O的切线.

(2)证明:如图所示,连接AD,则AD⊥BC.

∵AB=AC,∴DB=DC=BC.

∵∠CDF+∠C=90°,∠C+∠DAC=90°,∴∠CDF=∠DAC.

而∠DFC=∠ADC=90°,∴△CFD∽△CDA.

∴CD2=CF·AC.即BC2=4CF·AC.

(3)解:如图所示,连接OE,

∵∠CDF=15°,∴∠C=75°.∴∠DAC=15°.

∴∠OAE=30°=∠OEA.∴∠AOE=120°.

∴S△OAE=AE·OE·sin∠OEA=×2×OE·cos∠OEA·OE·sin∠OEA= 4,

∴S阴影部分=S扇形OAE-S△OAE=-4=-4.

23.(12分)如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线与AC,BC及AB的延长线分别相交于点D,E,F,☉O是△BEF的外接圆,   ∠EBF的平分线交EF于点G,交☉O于点H,连接BD,若BC=BF.

(1)求证:△ABC≌△EBF.

(2)试判断DB与☉O的位置关系,并说明理由.

(3)若AB=1,求线段BF和HG的长度.

(1)证明:∵∠ABC=90°,∴∠EBF=90°.

∵DF⊥AC,∴∠ADF=90°,∴∠C+∠A=∠A+∠AFD=90°,∴∠C=∠BFE.

在△ABC和△EBF中,∵∠C=∠AFE,BC=BF,∠ABC=∠EBF,∴△ABC≌   △EBF.

(2)解:BD与☉O相切.理由如下:如图所示,连接OB.

∵OB=OF,∴∠OBF=∠OFB.

∵∠ABC=90°,AD=CD,∴BD=CD,∴∠C=∠DBC.

∵∠C=∠BFE,∴∠DBC=∠OBF.

∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,即∠DBO=90°.

∵OB为☉O的半径,∴BD与☉O相切.

(3)解:如图所示,连接AE,FH,EH.由(1)知,△ABC≌△EBF,

∴AB=BE,BF=BC.

∵DF垂直平分AC,∴AE=CE=AB=,∴BF=BC=BE+EC=AB+CE=1+.

∵BH平分∠EBF,∴∠FBG=∠EBF=×90°=45°,

∴∠EGB=∠BFG+∠FBG=∠BFG+45°=∠C+45°=∠CAE+45°=∠CAE+   ∠EAB=∠CAB=∠BEG,

∴∠EGB=∠BEG,∴BG=BE=1.∵BH平分∠FBE,∴HF=HE.

∵∠FHE=180°-∠FBE=90°,∴∠HFE=45°,

∴∠HFB=45°+∠EFB=∠EGB=∠GEB=∠FHB,

∴∠HFB=∠FHB,即HB=BF=1+,∴HG=HB-GB=1+-1=.