数学八年级上册11.2.1 三角形的内角集体备课ppt课件

这是一份数学八年级上册11.2.1 三角形的内角集体备课ppt课件，共16页。PPT课件主要包含了探索性质，方法3剪拼法，方法2折叠法，平行线，已知△ABC，∵EF∥BC，延长BC到D，过C作CE∥BA，∴∠A∠1，∠B∠2等内容，欢迎下载使用。
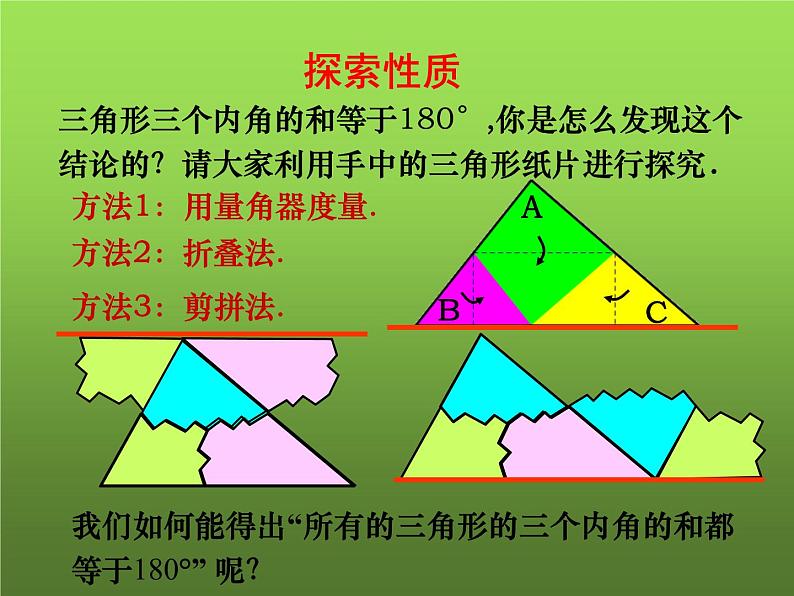
我们如何能得出“所有的三角形的三个内角的和都等于180°” 呢？
三角形三个内角的和等于180°,你是怎么发现这个结论的？请大家利用手中的三角形纸片进行探究．
方法1：用量角器度量.
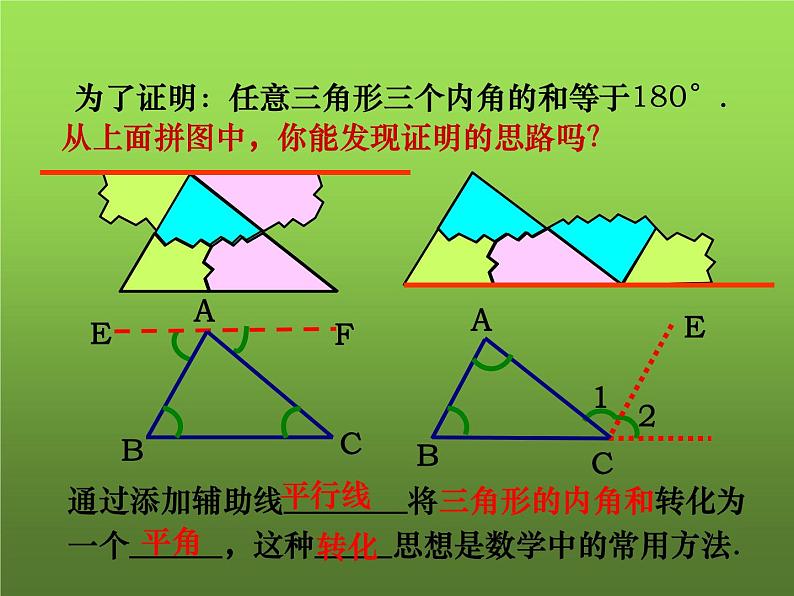
从上面拼图中，你能发现证明的思路吗？
为了证明：任意三角形三个内角的和等于180°.
通过添加辅助线________将三角形的内角和转化为一个______，这种_____思想是数学中的常用方法.
过点A作直线EF∥BC
∴∠2=∠B，∠3=∠C
∵∠1+∠2+∠3=180°（平角定义）
∴∠A+∠B+∠C=180°（等量代换）
求证：∠A +∠B +∠C =180°
（两直线平行,内错角相等）
(两直线平行，内错角相等)
(两直线平行，同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
本节课学习了哪些主要内容？1.为什么要用推理的方法证明三角形的内角和定理？2.你是怎么找到三角形内角和定理的证明思路的？3.如何应用三角形内角和定理解决问题？
通过添加平行线将三个内角的和转化为一个平角，这种转化思想是数学中的常用方法.
1、三角形的内角和定理：三角形内角和为180°
2、由三角形内角和等于180°，可得出
(1)一个三角形最多有一个直角、一个钝角、三个锐角，最少有两个锐角；
(2)一个三角形中至少有一个角小于或等于60°
如图△ABC中,CD平分∠ACB,DE∥BC,∠A＝70°,∠ADE＝50°, 求∠BDC的度数.
∴∠ACB=180 °-∠A-∠B
=180°-70°-50°
∴∠B=∠ADE＝50°
证明： ∵ DE ∥ BC （已知）∴ ∠ AED= ∠ C（两直线平行，同位角相等）∵ ∠ C=700（已知）∴ ∠ AED= 700 （等量代换）∵ ∠ A+ ∠ AED+ ∠ ADE=1800（三角形的内角和定理） ∠ A=600（已知）∴ ∠ ADE=1800—600—700=500（等量代换） 即∠ ADE= 500
如图在△ABC中，DE∥BC,∠A=60°, ∠C=70°. 求证： ∠ADE=50°
在△ＡＢＣ中，如果∠Ａ= ∠B= ∠C，那么△ＡＢＣ是什么三角形？
那么∠B=2x°,∠C=3x°
∴∠A=30°,∠B=60°,∠C=90°
所以△ＡＢＣ是直角三角形
X+2X+3X=180
三角形按角可以分为几类？
直角三角形ABC可以写成Rt△ABC.
夹直角的两边叫做直角边，直角的对边叫做斜边.
在Rt△ABC，∠C=90°，问：∠A与∠B有什么关系？请说明理由。解： ∠A与∠B互为余角理由：在△ABC中∠A+∠B =180°－∠C =180°－90° =90°
直角三角形的两个锐角互余.
在Rt△ABC 中， ∠A +∠B =90°．　　
有两个角互余的三角形是直角三角形吗？
已知：在△ABC中， ∠A +∠B =90°求证：△ABC是Rt△证明：在△ABC中∵ ∠A+∠B =90°（已知）∴∠C=180°–(∠A+∠B). =180°－90°=90°∴ △ABC是Rt△(直角三角形定义）也就是：有两个角互余的三角形是直角三角形
推理格式：在△ABC 中，∵∠A+∠B =90°，∴△ABC是直角三角形．
1.如图∠ACB=90°，CD⊥AB,垂足为D, ∠ACD与∠B有什么关系？为什么？
解： ∠ACD=∠B.理由：
∵CD⊥AB (已知）∴∠CDB=90°（垂直定义）在Rt△CDB中，∠2+∠B = 90°（直角三角形两锐角互余）在Rt△ACB中， ∠ 1+∠2= 90°∴∠1=∠B（同角的余角相等）
2.如图，∠C=90°，∠1=∠2，△ADE是直角三角形吗？为什么？
答:是直角三角形.理由：
在Rt△ABC中，∠A+∠2 = 90°（直角三角形两锐角互余）∵∠1=∠2 （已知）∴∠A+∠1 =90°（等量代换）∴△ADE是Rt三角形（两角互余的三角形是直角三角形）