







- 2.1坐标轴的平移与旋转(2) 课件+教案 课件 2 次下载
- 2.2参数方程(1) 课件+教案 课件 3 次下载
- 2.3应用举例 课件+教案 课件 2 次下载
- 3.1 复数的概念(2)课件-高教版中职数学职业模块工科类 课件 2 次下载
- 3.2 复数的运算(1)课件-高教版中职数学职业模块工科类 课件 2 次下载
高教版(中职)职业模块 工科类2.2.2 参数方程与普通方程的互化获奖ppt课件
展开【课题】 2.2 参数方程
【教学目标】
知识目标:
(1)掌握由曲线参数方程求曲线普通方程的基本方法,会将简单的参数方程化为普通方程.
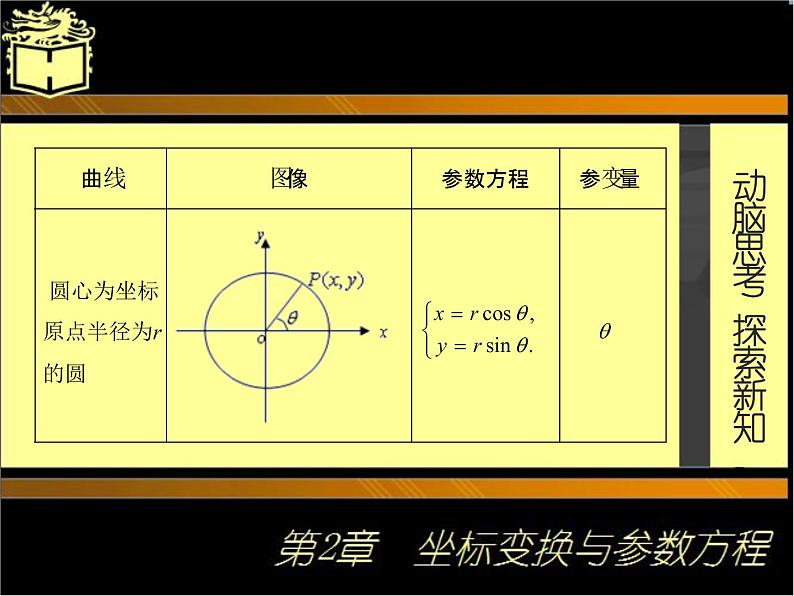
(2)掌握圆心为坐标原点半径为R的圆的参数方程.了解椭圆及其的参数方程,了解圆的渐开线、摆线的参数方程.
能力目标:
通过参数方程的学习,了解通过选取适当的参变量来研究曲线的特征的方法,提高分析和解决问题的能力.
【教学重点】
把曲线的参数方程化为普通方程.
【教学难点】
难点是曲线的参数方程化为普通方程.
【教学设计】
参数方程与普通方程的互化的重点是将参数方程化为普通方程.这是本章的教学重点和难点.有些参数方程是无法化为普通方程的.我们只能将一些简单的参数方程化为普通方程.常用的方法是代入消元法和加减消元法,加减消元法中经常使用一些三角恒等式.例题3的(1)和(2),在消去参数化为普通方程后,取值范围并没有改变.(3)中给出了参变量的取值范围,化为普通方程后,必须对变量或的取值进行限制,以保证方程是等价变换,不改变方程所表示图形的范围.生产实际中,会遇到用参数方程表示的曲线和用普通方程表示的曲线的交点的问题.解决这类问题的一般的方法是将参数方程代入普通方程,求出对应参变量的值.然后,再将参变量的取值代入参数方程,从而求出交点的坐标.需要注意的是,将参数方程代入普通方程求参变量的值时,必须考虑到各种情况,不要丢解.另一种方法是将参数方程化为普通方程,再联立两个普通方程为方程组,求方程组的解.椭圆、渐开线、摆线是与生产实际相联系的内容.在教学中,要特别注意不要加大难度和添加过多的内容,要考虑到学生的实际水平和生产的实际需要.
【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】
教 学 过 程 | 教师 行为 | 学生 行为 | 教学 意图 | 时间 | ||||||||||||||||||||||||
*揭示课题 2.2参数方程. |
介绍 |
了解 |
|
0 | ||||||||||||||||||||||||
*动脑思考 探索新知 实际应用中,主要是将参数方程化为普通方程.其核心是消去参变量,常用的方法是加减消元法、代入消元法. |
总结 归纳
|
思考 理解 记忆 |
带领 学生 总结 |
5 | ||||||||||||||||||||||||
*巩固知识 典型例题 例3 将下列参数方程化为普通方程. (1);(2);(3). 解 (1)由,代入,得 . (2)由得 , 由得 . 将上面的两个等式两边分别相加,利用三角恒等式,得 . 【小提示】 对于含有三角函数的参数方程,在利用加减消元法消去参数时,利用三角恒等式是经常使用的方法。 (3)由得,与方程两边对应相减,得,即. 由知参变量时,有,所以 (). 【注意】 将参数方程化为普通方程时,要注意参变量的取值范围和相应的取值范围,以及图形的范围. |
引领
讲解 说明
引领
|
观察
思考
主动 求解
观察
|
通过 例题 进一 步领 会
注意 观察 学生 是否 理解 知识 点
|
25 | ||||||||||||||||||||||||
*运用知识 强化练习 将参数方程化为普通方程: . |
提问 巡视 指导 |
动手 求解
|
了解 知识 掌握 情况 |
35 | ||||||||||||||||||||||||
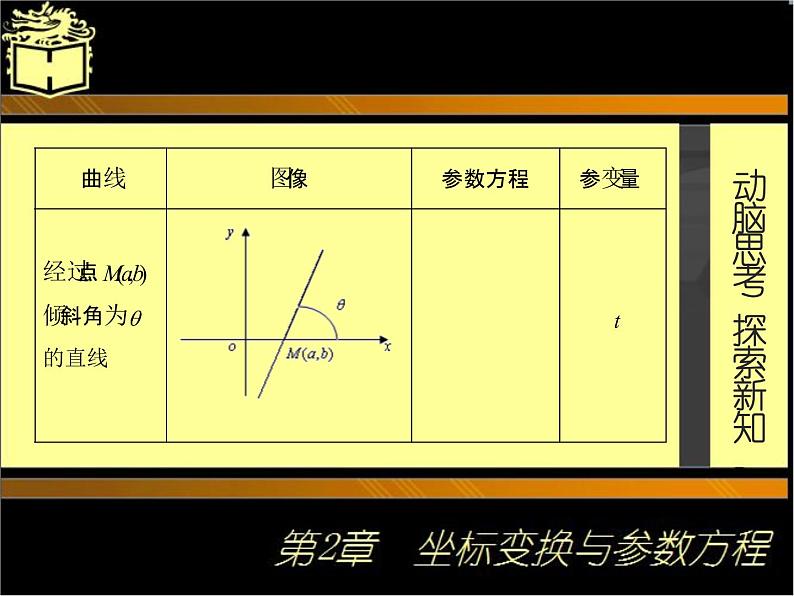
*动脑思考 探索新知 机械加工和数控编程常见的曲线,除了直线和圆外,还有一些曲线,例如圆的渐开线、摆线等齿轮轮廓曲线.现将常见曲线的参数方程列表如下:
说明: (1)把一根没有伸缩性的绳子绕在一个固定的圆盘上,将绳子的端点M拉紧并逐渐展开,展开时绳子的拉直部分始终保持与圆相切,这时绳子的端点M的轨迹叫做圆的渐开线,这个圆叫做渐开线的基圆. (2)一个定圆沿着一条定直线作无滑动滚动时,圆周上一点的轨迹叫做摆线(或旋轮线). |
总结 归纳
讲解 说明
|
思考 理解 记忆
思考 理解 记忆 |
带领 学生 总结 |
50 | ||||||||||||||||||||||||
*运用知识 强化练习 用“描点法”作出椭圆的图形. |
提问 巡视 指导 |
动手 求解
| 了解 学生 知识 掌握 情况 |
70 | ||||||||||||||||||||||||
*理论升华 整体建构 思考并回答下面的问题: 回顾常见曲线参数列表: 结论: 略 |
质疑
归纳强调
|
理解
强化 |
强调重点突破难点 |
75 | ||||||||||||||||||||||||
*归纳小结 强化思想 本次课学了哪些内容?重点和难点各是什么? |
引导 |
回忆 |
|
80 | ||||||||||||||||||||||||
*自我反思 目标检测 本次课采用了怎样的学习方法?你是如何进行学习的?你的学习效果如何? 将参数方程化为普通方程: . |
提问
巡视 指导 |
反思
动手 求解 |
检验 学习 效果
|
85 | ||||||||||||||||||||||||
*继续探索 活动探究 (1)读书部分:教材 (2)书面作业:教材习题2.2(必做);学习指导2.2(选做) (3)实践调查:通过自制模型演示,理解圆的渐开线、摆线的概念. |
说明 |
记录 |
分层次要求 |
90 |
【教师教学后记】
项目 | 反思点 |
学生知识、技能的掌握情况 | 学生是否真正理解有关知识; 是否能利用知识、技能解决问题; 在知识、技能的掌握上存在哪些问题; |
学生的情感态度 | 学生是否参与有关活动; 在教学活动中,是否认真、积极、自信; 遇到困难时,是否愿意通过自己的努力加以克服; |
学生思维情况 | 学生是否积极思考; 思维是否有条理、灵活; 是否能提出新的想法; 是否自觉地进行反思; |
学生合作交流的情况 | 学生是否善于与人合作; 在交流中,是否积极表达; 是否善于倾听别人的意见; |
学生实践的情况 | 学生是否愿意开展实践; 能否根据问题合理地进行实践; 在实践中能否积极思考; 能否有意识的反思实践过程的方面; |
高中数学高教版(中职)职业模块 财经、商贸与服务类2.2.2 算法程序框图的基本结构优质课件ppt: 这是一份高中数学高教版(中职)职业模块 财经、商贸与服务类2.2.2 算法程序框图的基本结构优质课件ppt,文件包含22算法的程序框图教案-高二下学期高教版中职数学职业模块财经商务与服务第二章算法与程序框图+docx、22算法的程序框图课件-高二下学期高教版中职数学职业模块财经商务与服务第二章算法与程序框图pptx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
数学职业模块 工科类第2章 坐标变换与参数方程2.3 应用举例精品课件ppt: 这是一份数学职业模块 工科类第2章 坐标变换与参数方程2.3 应用举例精品课件ppt,文件包含23应用举例课件-2020-2021学年高二下学期高教版中职数学职业模块工科类ppt、23应用举例教案-2020-2021学年高二下学期高教版中职数学职业模块工科类doc等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
高中数学高教版(中职)职业模块 工科类2.2.2 参数方程与普通方程的互化完整版ppt课件: 这是一份高中数学高教版(中职)职业模块 工科类2.2.2 参数方程与普通方程的互化完整版ppt课件,文件包含22参数方程1课件-2020-2021学年高二下学期高教版中职数学职业模块工科类ppt、22参数方程1教案-2020-2021学年高二下学期高教版中职数学职业模块工科类doc等2份课件配套教学资源,其中PPT共11页, 欢迎下载使用。












