




- 4.3 逻辑图与逻辑代数的运算律 课件+教案 课件 2 次下载
- 4.4 卡诺图及其应用(1) 课件+教案 课件 2 次下载
- 4.5 应用举例 课件+教案 课件 2 次下载
- 5.1 算法(1) 课件+教案 课件 3 次下载
- 5.1 算法(2) 课件+教案 课件 3 次下载
高中数学第4章 逻辑代数初步4.4 卡诺图及其应用4.4.2 卡诺图精品ppt课件
展开【课题】 4.4 卡诺图及其应用(二)
【教学目标】
知识目标:
掌握逻辑函数卡诺图的表示法,并会利用卡诺图进行逻辑式的化简.
能力目标:
通过对逻辑式化简的学习,学生的数学思维能力得到锻炼和提高.
【教学重点】
利用卡诺图进行逻辑式的化简.
【教学难点】
利用卡诺图进行逻辑式的化简.
【教学设计】
例2是作出三个变量的函数的卡诺图表示的题目.例3是根据卡诺图写成函数的最小项表达式的题目,需将逻辑常量1对应的项挑出来并写成逻辑和的形式.通过这两道例题,让学生熟悉函数的卡诺图表示.例4是利用卡诺图化简逻辑函数的示例,教学中要强调解题的步骤和方法,强调如何有效地圈完所有的“1”.教材中给出了利用卡诺图化简逻辑函数表达式的五个步骤,结合例5强化这些步骤.
【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】
教 学 过 程 | 教师 行为 | 学生 行为 | 教学 意图 | 时间 | ||||||||||||||||||||||||
*揭示课题 4.4卡诺图及其应用 |
介绍 |
了解 |
|
0 | ||||||||||||||||||||||||
*动脑思考 探索新知 将逻辑函数写成最小项表达式,在各最小项所对应的小方格内填入“1”,其他方格内填入“0”,得这个函数的卡诺图表示. |
详细分析讲解 |
思考
|
带领 学生 总结 |
5 | ||||||||||||||||||||||||
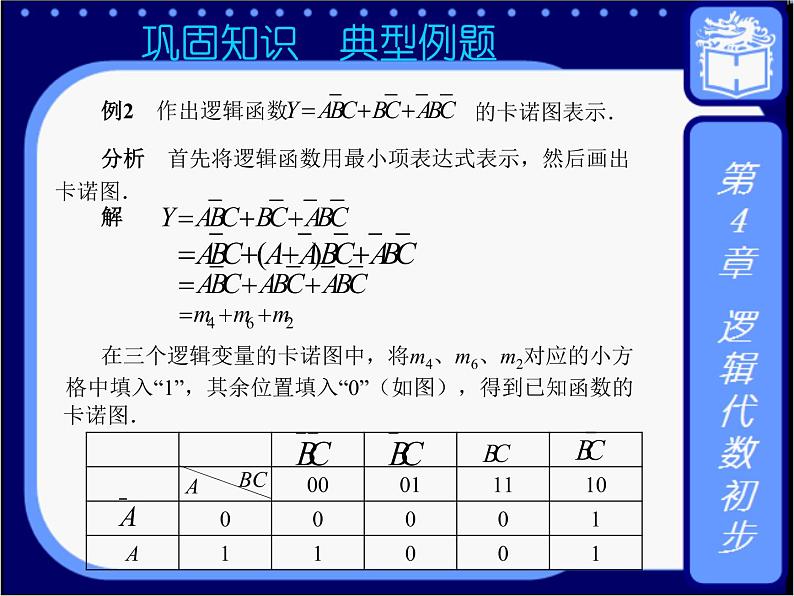
*巩固知识 典型例题 例2 作出逻辑函数的卡诺图表示. 分析 首先将逻辑函数用最小项表达式表示,然后画出卡诺图. 解
. 在三个逻辑变量的卡诺图中,将m4、m6、m2对应的小方格中填入“1”,其余位置填入“0”(如图),得到已知函数卡诺图.
|
引领
讲解
说明
|
观察
思考
主动 求解
|
通过 例题 进一 步领 会
|
25 | ||||||||||||||||||||||||
*动脑思考 探索新知 给出逻辑函数的最小项表达式,可以画出卡诺图,反过来,给出逻辑函数的卡诺图,可以写出逻辑函数的最小项表达式.方法是,将填1的方格对应的最小项写出来,然后将各项相加. |
详细分析讲解 总结 归纳 |
思考 理解 记忆
|
带领 学生 总结
|
30 | ||||||||||||||||||||||||
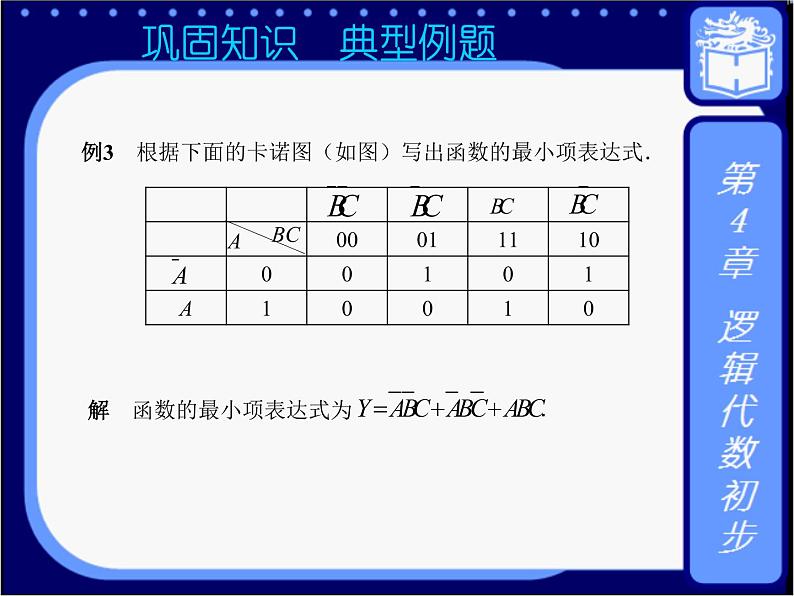
*巩固知识 典型例题 例3 根据下面的卡诺图(如图4-11)写出函数的最小项表达式.
图4-11 解 函数的最小项表达式为. |
引领
讲解 说明
|
观察
思考
主动 求解
|
通过 例题 进一 步领 会
|
35 | ||||||||||||||||||||||||
*运用知识 强化练习 1 画出下列函数的卡诺图: (1);(2). 2 根据下面的卡诺图写出函数的最小项表达式.
第2题图 |
提问 巡视 指导
|
动手 求解
|
及时 了解 学生 知识 掌握 情况 |
40 | ||||||||||||||||||||||||
*动脑思考 探索新知 由于卡诺图相邻的两个方格内,对应的是逻辑相邻的最小项,可以合并成一项,并消去以相反状态出现的1个变量(因子);相邻的四个最小项,可以消去2个变量;相邻的八个最小项,可以消去3个变量. |
详细分析讲解 总结 归纳 |
思考 理解 记忆
|
带领 学生 总结
|
45 | ||||||||||||||||||||||||
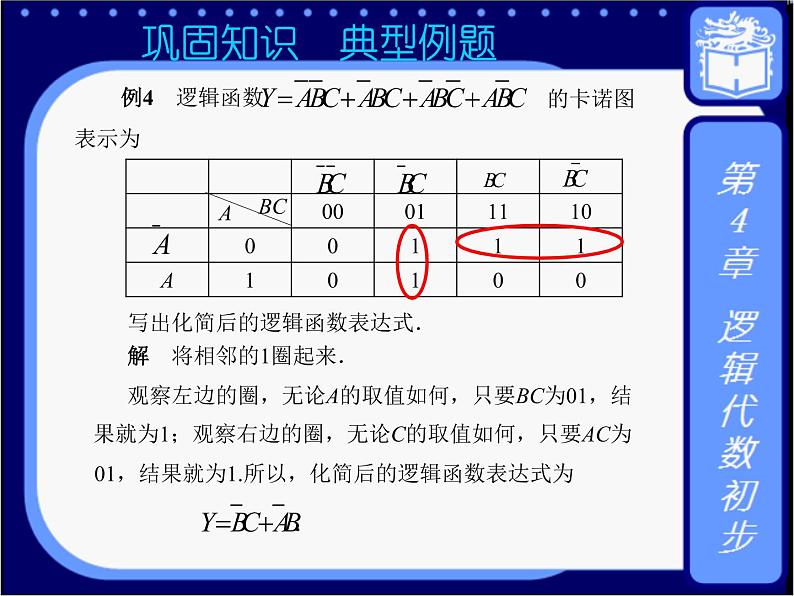
*巩固知识 典型例题 例4 逻辑函数的卡诺图表示为
图4-12 写出化简后的逻辑函数表达式. 解 将相邻的1圈起来.观察左边的圈,无论A的取值如何,只要BC为01,结果就为1;观察右边的圈,无论C的取值如何,只要AC为01,结果就为1.所以,化简后的逻辑函数表达式为 |
引领
讲解 说明
|
观察
思考
主动 求解
|
通过 例题 进一 步领 会
|
55 | ||||||||||||||||||||||||
*动脑思考 探索新知 “圈1”时需要注意: (1)圈内的相邻项,只能为2项、4项或8项,并且圈的个数尽量少; (2)有些方格可能多次被圈,但是每个圈内的方格,不能都是其他圈所圈过的. 利用卡诺图化简逻辑函数表达式的基本步骤是: (1)将表达式用最小项的和表示; (2)画出函数的卡诺图; (3)在卡诺图中“圈1”; (4)消去各圈中以相反状态出现的变量; (5)写出化简后的逻辑函数表达式. |
详细分析讲解 总结 归纳 |
思考 理解 记忆
|
带领 学生 总结
|
60 | ||||||||||||||||||||||||
*巩固知识 典型例题 例5 化简 解 . 对应的卡诺图(如图4-13)为
图4−13 观察上面的圈,无论B和C取值如何,只要A取0,结果就为1;观察中间的圈,无论B和A的取值如何,只要C取1,结果就为1.因此, . |
引领
讲解 说明
|
观察
思考
主动 求解
|
通过 例题 进一 步领 会
|
65 | ||||||||||||||||||||||||
*运用知识 强化练习 化简. |
提问 巡视 指导 |
动手 求解 | 了解 学生 知识 掌握 |
70 | ||||||||||||||||||||||||
*理论升华 整体建构 思考并回答下面的问题: 利用卡诺图化简逻辑函数表达式的基本步骤是什么? 结论: 利用卡诺图化简逻辑函数表达式的基本步骤是: (1)将表达式用最小项的和表示; (2)画出函数的卡诺图; (3)在卡诺图中“圈1”; (4)消去各圈中以相反状态出现的变量; (5)写出化简后的逻辑函数表达式. |
质疑
强调 |
回答
强化 |
师生共同归纳强调重点 |
75 | ||||||||||||||||||||||||
*归纳小结 强化思想 本次课学了哪些内容?重点和难点各是什么? |
引导 |
回忆 |
|
80 | ||||||||||||||||||||||||
*自我反思 目标检测 本次课采用了怎样的学习方法?你是如何进行学习的?你的学习效果如何? 化简. |
提问 巡视 指导 |
反思 动手 求解 |
检验 学习 效果 |
85 | ||||||||||||||||||||||||
*继续探索 活动探究 (1)读书部分:教材 (2)书面作业:教材习题4.4(必做);学习与训练训练题4.4(选做) (3)实践调查:画出一道逻辑函数的卡诺图 |
说明 |
记录 |
分层次要求 |
90 |
【教师教学后记】
项目 | 反思点 |
学生知识、技能的掌握情况 | 学生是否真正理解有关知识; 是否能利用知识、技能解决问题; 在知识、技能的掌握上存在哪些问题; |
学生的情感态度 | 学生是否参与有关活动; 在教学活动中,是否认真、积极、自信; 遇到困难时,是否愿意通过自己的努力加以克服; |
学生思维情况 | 学生是否积极思考; 思维是否有条理、灵活; 是否能提出新的想法; 是否自觉地进行反思; |
学生合作交流的情况 | 学生是否善于与人合作; 在交流中,是否积极表达; 是否善于倾听别人的意见; |
学生实践的情况 | 学生是否愿意开展实践; 能否根据问题合理地进行实践; 在实践中能否积极思考; 能否有意识的反思实践过程的方面; |
高教版(中职)职业模块 财经、商贸与服务类4.4 计划的调整与优化精品课件ppt: 这是一份高教版(中职)职业模块 财经、商贸与服务类4.4 计划的调整与优化精品课件ppt,文件包含44计划的调整与优化课件-高二下学期高教版中职数学职业模块财经商务与服务第四章算编制计划的原理与方法pptx、44计划的调整与优化教案-高二下学期高教版中职数学职业模块财经商务与服务第四章算编制计划的原理与方法docx等2份课件配套教学资源,其中PPT共7页, 欢迎下载使用。
高教版(中职)职业模块 财经、商贸与服务类4.3.2 横道图试讲课ppt课件: 这是一份高教版(中职)职业模块 财经、商贸与服务类4.3.2 横道图试讲课ppt课件,文件包含43网络图与横道图课件-高二下学期高教版中职数学职业模块财经商务与服务第四章算编制计划的原理与方法pptx、43网络图与横道图教案-高二下学期高教版中职数学职业模块财经商务与服务第四章算编制计划的原理与方法docx等2份课件配套教学资源,其中PPT共12页, 欢迎下载使用。
高中数学高教版(中职)职业模块 工科类4.4.2 卡诺图获奖课件ppt: 这是一份高中数学高教版(中职)职业模块 工科类4.4.2 卡诺图获奖课件ppt,文件包含44卡诺图及其应用1课件-高二下学期高教版中职数学职业模块工科类ppt、44卡诺图及其应用1教案-高二下学期高教版中职数学职业模块工科类doc等2份课件配套教学资源,其中PPT共14页, 欢迎下载使用。












