江苏省淮安市涟水县安东学校2022-2023学年八年级上学期第一次质检数学试卷(含答案)

这是一份江苏省淮安市涟水县安东学校2022-2023学年八年级上学期第一次质检数学试卷(含答案)，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
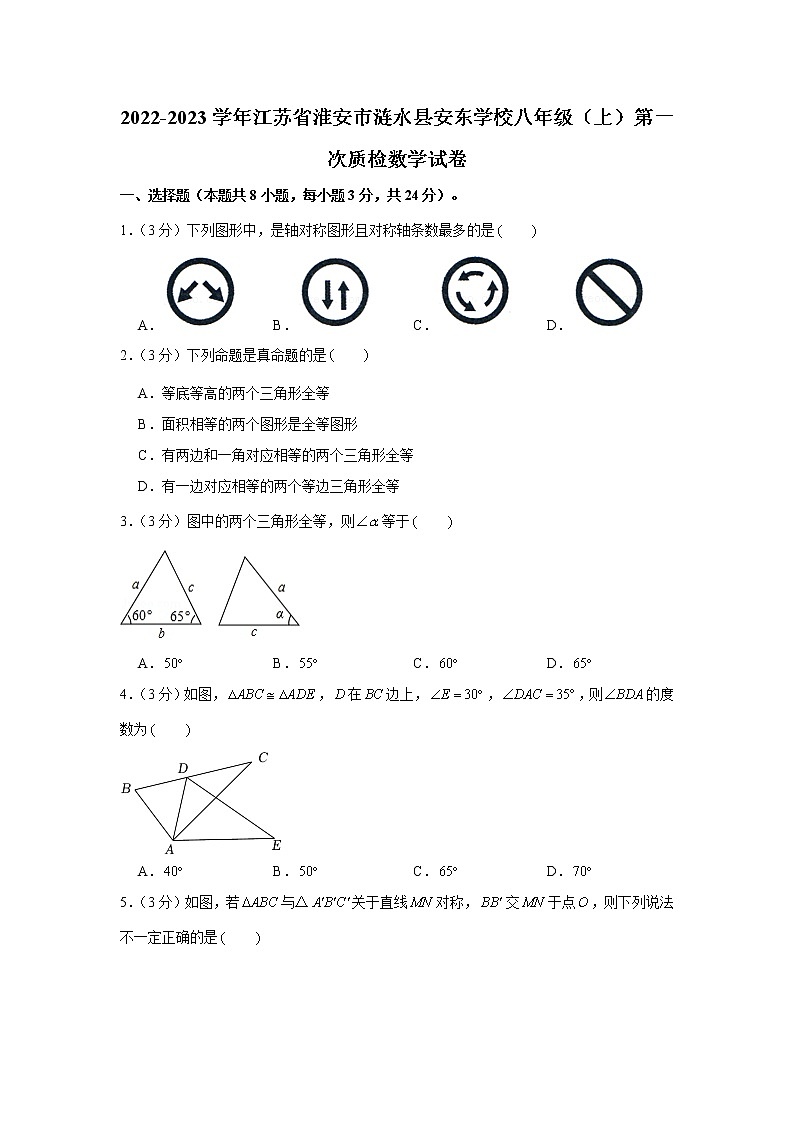
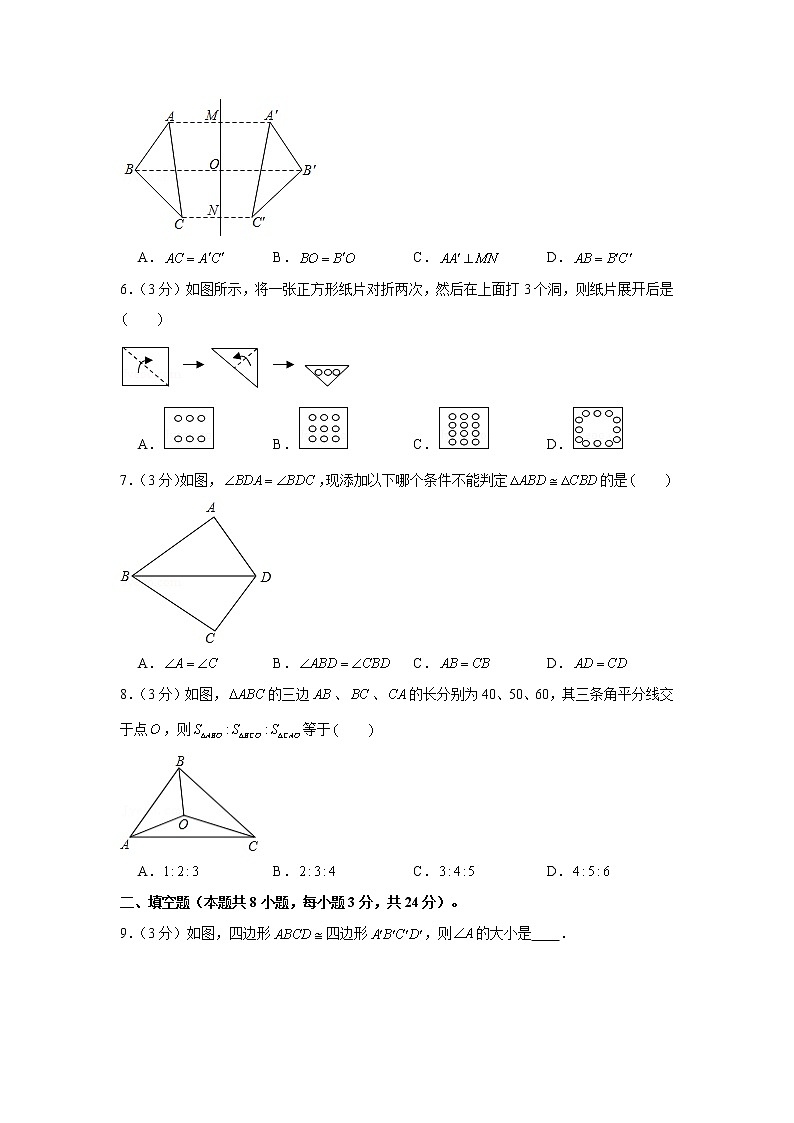
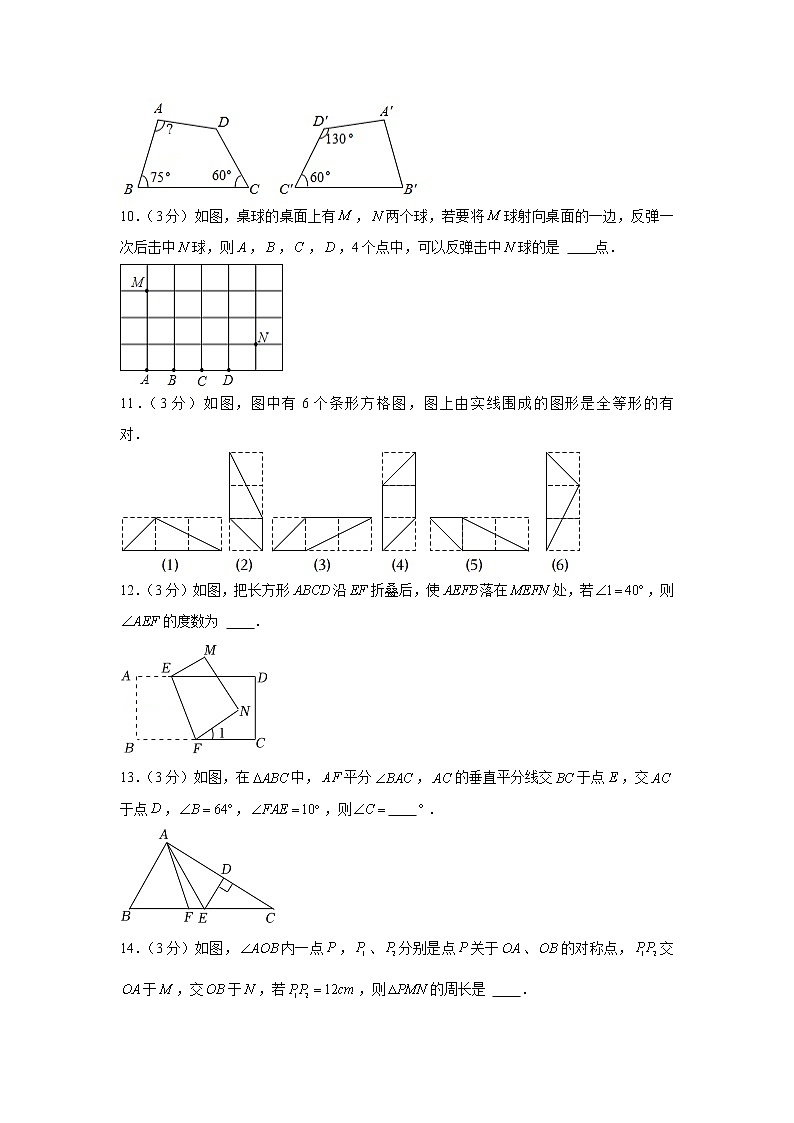
2022-2023学年江苏省淮安市涟水县安东学校八年级（上）第一次质检数学试卷一、选择题（本题共8小题，每小题3分，共24分）。1．（3分）下列图形中，是轴对称图形且对称轴条数最多的是　　A． B． C． D．2．（3分）下列命题是真命题的是　　A．等底等高的两个三角形全等 B．面积相等的两个图形是全等图形 C．有两边和一角对应相等的两个三角形全等 D．有一边对应相等的两个等边三角形全等3．（3分）图中的两个三角形全等，则等于　　A． B． C． D．4．（3分）如图，，在边上，，，则的度数为　　A． B． C． D．5．（3分）如图，若与△关于直线对称，交于点，则下列说法不一定正确的是　　A． B． C． D．6．（3分）如图所示，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是　　A． B． C． D．7．（3分）如图，，现添加以下哪个条件不能判定的是　　A． B． C． D．8．（3分）如图，的三边、、的长分别为40、50、60，其三条角平分线交于点，则等于　　A． B． C． D．二、填空题（本题共8小题，每小题3分，共24分）。9．（3分）如图，四边形四边形，则的大小是　　．10．（3分）如图，桌球的桌面上有，两个球，若要将球射向桌面的一边，反弹一次后击中球，则，，，，4个点中，可以反弹击中球的是 　　点．11．（3分）如图，图中有6个条形方格图，图上由实线围成的图形是全等形的有 　　对．12．（3分）如图，把长方形沿折叠后，使落在处，若，则的度数为 　　．13．（3分）如图，在中，平分，的垂直平分线交于点，交于点，，，则　　．14．（3分）如图，内一点，、分别是点关于、的对称点，交于，交于，若，则的周长是 　　．15．（3分）如图，在四边形中，，，连接，，，若是边上一动点，则的最小值为　　．16．（3分）如图所示，已知的面积是26，、分别平分和，于，且，则的周长是 　　．三、解答题（本题共9小题，共72分）。17．（8分）如图，在长度为1个单位长度的小正方形组成的正方形网格中，点、、在小正方形的顶点上．（1）在图中画出与关于直线成轴对称的△；（2）线段被直线　 　；（3）的面积为　 　；（4）在直线上找一点，使的长最短．18．（6分）如图，，，．求证：．19．（6分）如图，在中，，，．是的角平分线，点在边上，．求的周长．20．（6分）如图，在中，是的垂直平分线，且分别交，于、两点，，，求的度数．21．（8分）如图，是的角平分线，、分别是和的高．（1）试说明垂直平分；（2）若，，，求的长．22．（8分）如图，已知，，．求证：．23．（8分）如图，在中，，，为延长线上一点，点在边上，且，连接、、．（1）求证：；（2）若，求的度数．24．（10分）如图，已知，，平分，平分，点恰好在上．（1）求证：点为中点．（2）试探究线段、、的数量关系．25．（12分）在内有一点．过点分别作，，垂足分别为，．且，点，分别在边和上．（1）如图1，若，．．则　　；（2）如图2，若，，求的长；（3）如图3，若，，猜想，，三条线段间具有的数量关系，并说明你的结论成立的理由．
2022-2023学年江苏省淮安市涟水县安东学校八年级（上）第一次质检数学试卷参考答案与试题解析一、选择题（本题共8小题，每小题3分，共24分）。1．（3分）下列图形中，是轴对称图形且对称轴条数最多的是　　A． B． C． D．【分析】根据轴对称图形的概念求解即可．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线对称．【解答】解：．是轴对称图形，共有1条对称轴；．不是轴对称图形，没有对称轴；．不是轴对称图形，没有对称轴；．是轴对称图形，共有2条对称轴．故选：．2．（3分）下列命题是真命题的是　　A．等底等高的两个三角形全等 B．面积相等的两个图形是全等图形 C．有两边和一角对应相等的两个三角形全等 D．有一边对应相等的两个等边三角形全等【分析】利用全等三角形的判定方法一一判断即可．【解答】解：、等底等高的两个三角形全等，错误，不一定全等，本选项不符合题意；、面积相等的两个图形是全等图形．错误，不一定全等，本选项不符合题意；、有两边和一角对应相等的两个三角形全等．错误，不一定全等，本选项不符合题意；、有一边对应相等的两个等边三角形全等．正确，本选项符合题意．故选：．3．（3分）图中的两个三角形全等，则等于　　A． B． C． D．【分析】由全等三角形的对应角相等可求得答案．【解答】解：两三角形全等，、两边的夹角相等，，故选：．4．（3分）如图，，在边上，，，则的度数为　　A． B． C． D．【分析】根据全等三角形的性质及三角形外角性质求解即可．【解答】解：，，，，，，故选：．5．（3分）如图，若与△关于直线对称，交于点，则下列说法不一定正确的是　　A． B． C． D．【分析】根据轴对称的性质对各选项分析判断后利用排除法求解．【解答】解：与△关于直线对称，，，，故、、选项正确，不一定成立，故选项错误，所以，不一定正确的是．故选：．6．（3分）如图所示，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是　　A． B． C． D．【分析】结合空间思维，分析折叠的过程及打孔的位置，易知展开的形状．【解答】解：当正方形纸片两次沿对角线对折成为一直角三角形时，在平行于斜边的位置上打3个洞，则直角顶点处完好，即原正方形中间无损，且有12个洞．故选：．7．（3分）如图，，现添加以下哪个条件不能判定的是　　A． B． C． D．【分析】利用三角形全等的判定方法对各选项进行判断．【解答】解：，，当添加时，可根据“”判断；当添加时，可根据“”判断；当添加时，可根据“”判断．故选：．8．（3分）如图，的三边、、的长分别为40、50、60，其三条角平分线交于点，则等于　　A． B． C． D．【分析】作于，于，于，根据角平分线的性质得到，根据三角形的面积公式计算即可．【解答】解：作于，于，于，三条角平分线交于点，，，，，，故选：．二、填空题（本题共8小题，每小题3分，共24分）。9．（3分）如图，四边形四边形，则的大小是　　．【分析】利用全等图形的定义可得，然后再利用四边形内角和为可得答案．【解答】解：四边形四边形，，，故答案为：．10．（3分）如图，桌球的桌面上有，两个球，若要将球射向桌面的一边，反弹一次后击中球，则，，，，4个点中，可以反弹击中球的是 　点　点．【分析】要击中点，则需要满足点反弹后经过的直线过点，画出反射路线即可得出答案．【解答】解：可以瞄准点击球．故答案为：点．11．（3分）如图，图中有6个条形方格图，图上由实线围成的图形是全等形的有 　2　对．【分析】设每个小方格的边长为1，分别表示出第个图形的各边长，再根据全等形是可以完全重合的图形进行判定即可．【解答】解：设每个小方格的边长为1，则：（1）的各边分别是3，，；（2）的各边长分别是：，1，，2；（3）的各边长分别是：，1，，2；（4）的各边长分别是：2，，2，；（5）的各边长分别是：，1，，2；（6）的各边分别是3，，；故（1）（6）是全等形，（2）（3）（5）是全等形．故答案为：2．12．（3分）如图，把长方形沿折叠后，使落在处，若，则的度数为 　　．【分析】根据图形全等的性质，由题意得四边形四边形，，得．由，得，推断出．根据平行线的性质，由，得，从而解决此题．【解答】解：由题意得，四边形四边形，．．，．．．，．．故答案为：．13．（3分）如图，在中，平分，的垂直平分线交于点，交于点，，，则　32　．【分析】根据线段垂直平分线的性质可得，从而可得，进而可得，然后利用角平分线的定义可得，最后利用三角形内角和定理进行计算即可解答．【解答】解：是的垂直平分线，，，，，平分，，，，，，故答案为：32．14．（3分）如图，内一点，、分别是点关于、的对称点，交于，交于，若，则的周长是 　　．【分析】根据轴对称的性质的相等关系进行等量代换，便可知与的周长是相等的．【解答】解：和分别是和的对称轴，，；，的周长为．故答案为：．15．（3分）如图，在四边形中，，，连接，，，若是边上一动点，则的最小值为　10　．【分析】根据垂线段最短，当垂直于的时候，的长度最小，则结合已知条件，利用三角形的内角和定理推出，由角平分线性质即可得，由的长可得的长．【解答】解：根据垂线段最短，当的时候，的长度最小，，即，又，，又，，又，，，又，．故答案为：10．16．（3分）如图所示，已知的面积是26，、分别平分和，于，且，则的周长是 　26　．【分析】作于，于，连接，根据角平分线的性质分别求出，，根据三角形的面积公式计算．【解答】解：作于，于，连接，平分，，，，同理，，的面积的面积的面积的面积，的周长，故答案为：26．三、解答题（本题共9小题，共72分）。17．（8分）如图，在长度为1个单位长度的小正方形组成的正方形网格中，点、、在小正方形的顶点上．（1）在图中画出与关于直线成轴对称的△；（2）线段被直线　垂直平分　；（3）的面积为　 　；（4）在直线上找一点，使的长最短．【分析】（1）根据网格结构找出点、关于直线的对称点、的位置，在于点（即顺次连接即可；（2）根据轴对称的性质，对称轴垂直平分对称点的连线；（3）利用所在的矩形的面积减去四周三个小直角三角形的面积，列式计算即可得解；（4）根据轴对称确定最短路线问题，连接与对称轴的交点即为所求的点．【解答】解：（1）△如图所示； （2）线段被直线垂直平分； （3）的面积，，，； （4）点如图所示．故答案为：（2）垂直平分；（3）3．18．（6分）如图，，，．求证：．【分析】先证出，再由证明．【解答】证明：，，在和中，，，19．（6分）如图，在中，，，．是的角平分线，点在边上，．求的周长．【分析】根据线段的和差得到，根据角平分线的定义，利用证明，得，则的周长，即可得出答案．【解答】解：，，，，，是的角平分线，，在和中，，，，的周长，答：的周长是．20．（6分）如图，在中，是的垂直平分线，且分别交，于、两点，，，求的度数．【分析】先利用三角形内角和定理求出，从而利用三角形外角的性质可得，然后利用线段垂直平分线的性质，从而利用等腰三角形的性质可得，最后进行计算即可解答．【解答】解：，，，，是的垂直平分线，，，，的度数为．21．（8分）如图，是的角平分线，、分别是和的高．（1）试说明垂直平分；（2）若，，，求的长．【分析】（1）由角平分线的性质得，再由，得，从而证明结论；（2）根据三角形的面积公式，代入计算即可．【解答】（1）证明：是的角平分线，、分别是和的高，，在与中，，，，，垂直平分；（2）解：，，，，．22．（8分）如图，已知，，．求证：．【分析】先证明，然后根据“”可判断．【解答】证明：，，即，在和中，，．23．（8分）如图，在中，，，为延长线上一点，点在边上，且，连接、、．（1）求证：；（2）若，求的度数．【分析】（1）利用即可证明；（2）由全等三角形的性质得，再由外角的性质求出的度数，即可确定出的度数．【解答】（1）证明：，，，在和中，，；（2）解：，，，由（1）得：，，为的外角，，．24．（10分）如图，已知，，平分，平分，点恰好在上．（1）求证：点为中点．（2）试探究线段、、的数量关系．【分析】（1）过点作于，根据角平分线上的点到角的两边距离相等可得，，从而得到，然后根据线段中点的定义解答；（2）利用“”证明和全等，根据全等三角形对应边相等可得，同理可证，然后根据证明即可．【解答】（1）证明：如图，过点作于，平分，平分，，，，点为中点； （2）解：在和中，，，，同理可证，，，．25．（12分）在内有一点．过点分别作，，垂足分别为，．且，点，分别在边和上．（1）如图1，若，．．则　50　；（2）如图2，若，，求的长；（3）如图3，若，，猜想，，三条线段间具有的数量关系，并说明你的结论成立的理由．【分析】（1）根据平行四边形的判定和性质解答即可；（2）根据题目中的条件和，可以证明，从而可以得到；（3）作辅助线，过点作，交于点，从而可以得到，然后即可得到，，再根据题目中的条件可以得到，即可得到，然后即可得到，，具有的数量关系．【解答】解：（1），，四边形是平行四边形，，，，，，故答案为：50．（2），，，在和中，，．；（3），理由：过点作，交于点，在和中，，，，．，，．，．在和中，，．，．