数学职业模块 财经、商贸与服务类1.1.2 逻辑联结词一等奖课件ppt

这是一份数学职业模块 财经、商贸与服务类1.1.2 逻辑联结词一等奖课件ppt，文件包含11命题逻辑课件-高二下学期高教版中职数学职业模块财经商务与服务第一章命题逻辑与条件判断pptx、11命题逻辑教案-高二下学期高教版中职数学职业模块财经商务与服务第一章命题逻辑与条件判断docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。

1.1 命题逻辑
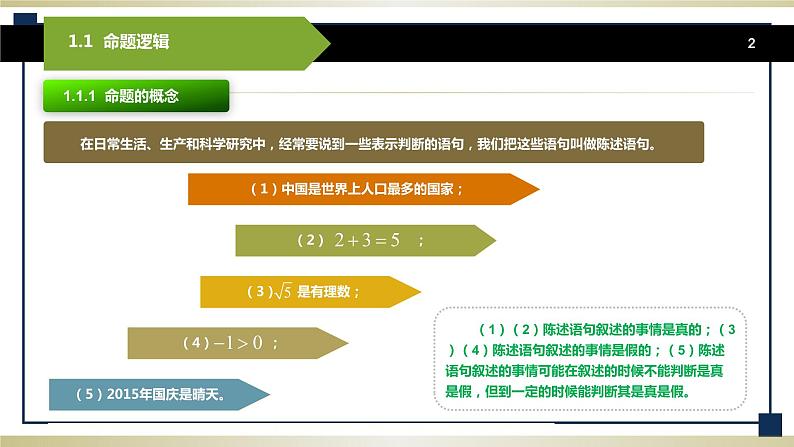
1.1.1 命题的概念
在日常生活、生产和科学研究中，经常要说到一些表示判断的语句，我们把这些语句叫做陈述语句。
（5）2015年国庆是晴天。
（1）中国是世界上人口最多的国家；
（1）（2）陈述语句叙述的事情是真的；（3）（4）陈述语句叙述的事情是假的；（5）陈述语句叙述的事情可能在叙述的时候不能判断是真是假，但到一定的时候能判断其是真是假。
1.1 命题逻辑
命题-一个能判断真假的陈述语句
真命题：一个命题叙述的事情如果是真的。
假命题：一个命题叙述的事情如果是假的。
1.1 命题逻辑
例题解析
解 （1）x取值不确定，是一个不能确定真假的陈述句，所以不是命题．（2）此句是一个祈使句，不是陈述句，所以不是命题．（3）此句是一个陈述句，并且叙述的事情是真的，所以是命题，而且是真命题．（4）此句是一个陈述句，但叙述的事情是假的，所以是命题，而且是假命题．（5）对于该语句，若其叙述的事情为“真”，即“我正在说假话” 为真，则这句话也应是假话，所以应为假命题，与假设矛盾；反之，若其叙述的事情为“假”，即“我正在说假话”为假，也就是“我正在说真话”，则这句话也应是真话，所以应为真命题，与假设矛盾．于是，这句话的真假无法确定，所以不是命题．
1.1 命题逻辑
总 结
判断一个语句是否是命题，首先要判断它是否是陈述语句，然后判断它能否辨别真假。
由真推出假，又由假推出真的陈述语句
“悖论”
1.1 命题逻辑
1.1.2 逻辑联结词
简单命题
如果一个命题不能分解成更简单的命题，则这个命题称为简单命题（或原子命题）。
复合命题
由简单命题通过加了诸如“当且仅当”“且”“或”“不是”“如果……那么……”等这样的连词或否定词得到的，这些词称为联结词．用一些联结词把一些简单命题连接起来组成的新命题叫做复合命题.
命题的三种运算
析取联结词
合取联结词
否定联结词
1.1 命题逻辑
1．合取联结词
p且q的真值表
1.1 命题逻辑
例题解析
1.1 命题逻辑
例题解析
1.1 命题逻辑
2．析取联结词
p或q的真值表
1.1 命题逻辑
例题解析
1.1 命题逻辑
例题解析
例5 用符号表示下列复合命题。 （1）实数a的绝对值等于a或 -a；（2）x＜3或x=5。
1.1 命题逻辑
3．否定联结词
非p真值表
1.1 命题逻辑
例题解析
1.1 命题逻辑
例题解析
例7 写出下列陈述语句的否定形式。（1） p：方程（x+1）2=0的解是x=-1； （2）q： a，b都是1 ；（3）r：x＞5.
1.1 命题逻辑