专题十六 直线与直线、直线与平面、平面与平面所成的角（B卷·能力提升）-【中职专用】高二数学同步单元测试AB卷（高教版·基础模块下册）

这是一份专题十六 直线与直线、直线与平面、平面与平面所成的角（B卷·能力提升）-【中职专用】高二数学同步单元测试AB卷（高教版·基础模块下册），文件包含专题十六直线与直线直线与平面平面与平面所成的角B卷·能力提升解析版docx、专题十六直线与直线直线与平面平面与平面所成的角B卷·能力提升原卷版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
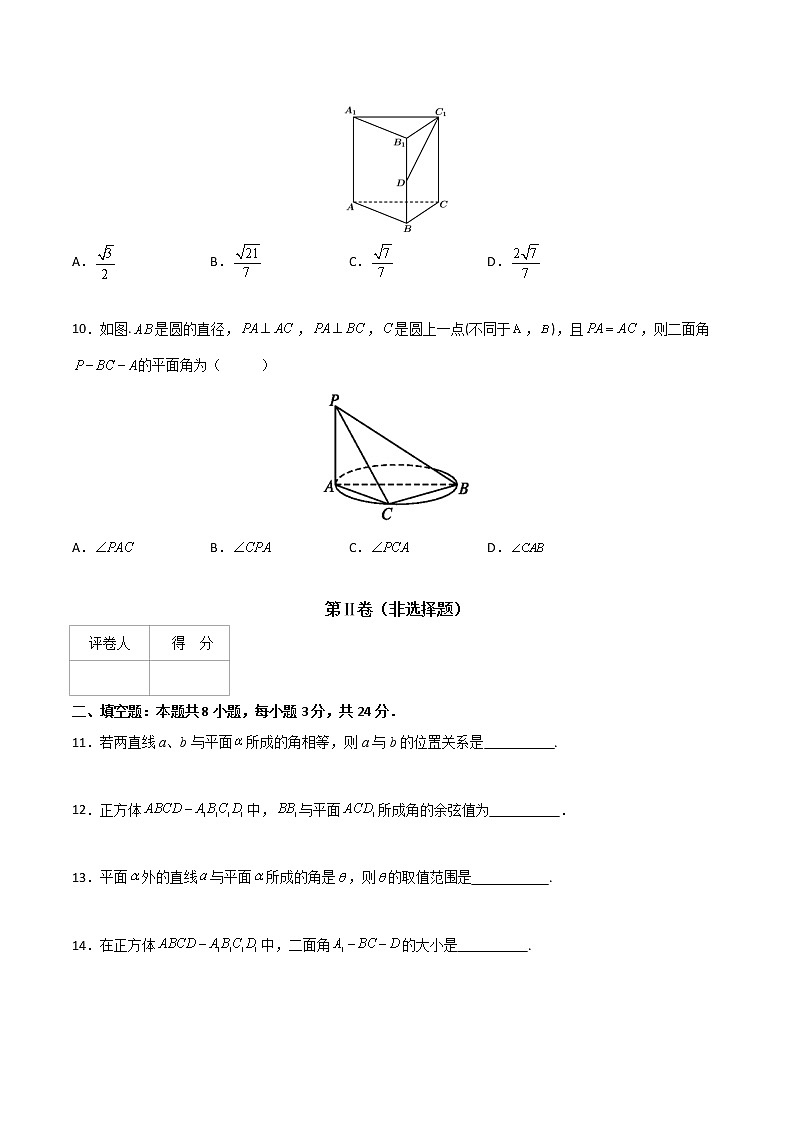
9.3 直线与直线、直线与平面、平面与平面所成的角（B卷·能力提升）学校:___________姓名：___________班级：___________考号：___________满分：100分   考试时间：100分钟题号一二三总分得分    注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上 第Ⅰ卷（选择题）评卷人  得  分   一、选择题：本题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．下列说法：①两个相交平面所组成的图形叫做二面角；②二面角的平面角是从棱上一点出发，分别在两个面内作射线所成的角；③二面角的大小与其平面角的顶点在棱上的位置有关系．  其中正确的个数是（       ）A．0 B．1 C．2 D．3【答案】A【解析】根据二面角的定义知①两个相交的半平面所组成的图形叫做二面角，故错误；②二面角的平面角是从棱上一点出发，分别在两个面内作棱的垂线所成的角，故错误；③二面角的大小与其平面角的顶点在棱上的位置无关，故错误．所以①②③都不正确．故选：A．2．在正方体中，则直线和夹角的余弦值为（ ）A． B． C． D．【答案】C【解析】如图所示，在正方体，连接，可得，则异面直线和所成的角，即为直线和所成的角，即异面直线和所成的角，在中，可得，所以，则，故选：C.3．在长方体中，，，，直线与平面所成的角是（       ）A．45°            B．90°             C．正切值为2           D．正切值为【答案】A【解析】长方体中，直线平面，所以就是直线与平面所成的角，在中，，， 所以，所以，故选：A.4．一条直线和平面所成角为，那么的取值范围是（       ）A．(0°，90°)         B．[0°，90°]          C．(0°，90°]        D．[0°，180°]【答案】B【解析】当直线和平面垂直时，直线和平面所成的角为，当直线与平面斜交时，直线和平面所成的角为锐角，当直线与平面平行或直线在平面内时，直线和平面所成的角为，所以直线和平面所成的角θ的取值范围是[0°，90°]，选B.5．在长方体中，，，则二面角的正切值为（       ）A． B． C． D．【答案】D【解析】∵，，由二面角的平面角的定义知，就是二面角的平面角，又，所以 ，故选：D.6．直线a与平面α所成的角为50°，直线b∥a，则直线b与平面α所成的角等于 (　　)A．40° B．50° C．90° D．150°【答案】B【解析】两条直线平行，它们与同一平面所成的角相等，直线a与平面α所成的角为50°，直线b∥a，则直线b与平面α所成的角等于，选B.7．若一个正四棱锥的侧棱和底面边长相等，则该正四棱锥的侧棱和底面所成的角为（       ）A．30° B．45° C．60° D．90°【答案】B【解析】正四棱锥 ，连接底面对角线， ，易知为等腰直角三角形.中点为 ，又正四棱锥知：底面 即 为所求角为 ，故选B.8．在正四面体A－BCD中，二面角A－CD－B的平面角的余弦值为（       ）A． B． C． D．【答案】B【解析】由A－BCD为正四面体知：若E为CD中点，连接AE、BE，则，而，∴面，即有为二面角A－CD－B的平面角，设正四面体的棱长为1，即， ∴在△中，作于H，则，而且，可得，∴.故选：B.9．如图，在正三棱柱中，，，点D是侧棱的中点，则直线与平面所成角的正弦值为（       ）A． B． C． D．【答案】B【解析】平面，与平面所成的角为.又，，可得，而平面平面，与平面所成角的正弦值为，故应选：B.10．如图.是圆的直径，，，是圆上一点(不同于，)，且，则二面角的平面角为（       ）A． B． C． D．【答案】C【解析】∵是圆上一点(不同于，)，是圆的直径，∴，，，即面，而面，∴，又面面，，∴由二面角的定义：为二面角的平面角，故选：C.第Ⅱ卷（非选择题）评卷人  得  分   二、填空题：本题共8小题，每小题3分，共24分．11．若两直线a、b与平面所成的角相等，则a与b的位置关系是          .【答案】平行、相交或异面【解析】若，显然a、b与平面所成的角相等；若a、b为圆锥的两条母线所在的直线，显然a、b与平面所成的角相等，此时a、b为相交直线；若a、b为异面直线，若满足，此时a、b与平面所成的角相等，均为0，故a与b的位置关系是平行、相交或异面，故答案为：平行、相交或异面．12．正方体中，与平面所成角的余弦值为          ．【答案】【解析】设上下底面的中心分别为O1，O，则O1O与平面ACD1所成角就是BB1与平面ACD1所成角，cos∠O1OD1=．13．平面外的直线与平面所成的角是，则的取值范围是           .【答案】【解析】直线在平面外包含两种情况：直线与平面相交、直线与平面平行.当直线与平面相交时，，当直线与平面平行时，，所以的取值范围为，故答案为．14．在正方体中，二面角的大小是          . 【答案】【解析】在正方体中，平面，所以，所以是二面角的平面角，在直角中，，所以，故答案为：．15．已知正四棱锥的侧棱长为，侧棱与底面所成的角为60°，则该四棱锥的高为           ．【答案】3【解析】如图，过点S作平面，连接，就是侧棱与底面所成的角，则，，故答案为：3．16．在正方体上，a，b是两条异面直线的面对角线，则它们所成的角大小可能为           .【答案】或【解析】正方体的面对角线成异面直线的，分平行的面和相交的面两类，如图找两对代表进行计算：1.异面直线与，其所成的角即为直线与所成的角，；2.异面直线与，其所成的角即为直线与所成的角，，故答案为：或. 17．已知二面角的大小为60°，若直线，直线，则异面直线，所成的角是          .【答案】【解析】如图，，，作于，于，作于，则，所以为二面角的平面角，则，所以，所以所成角为，则异面直线，所成的角为，故答案为：．18．在三棱锥中，平面，，则二面角的大小为           .【答案】【解析】因为平面，所以所以为二面角的平面角，又，所以二面角的大小为，故答案为：．评卷人  得  分   三、解答题：本题共6小题，共46分，解答时应写出文字说明、证明过程或者演算步骤.19．（6分）在棱长为1的正方体中，求异面直线与所成的角.【答案】【解析】解：连接，因为，，所以四边形是平行四边形，所以，所以或其补角即为异面直线与所成的角，连接，由正方体的棱长为可得，所以，所以异面直线与所成的角为． 20．（6分）在正方体中，为侧面的中心，求与平面所成角的正弦值.【答案】【解析】解：取中点，连接为侧面的中心，平面与平面所成角即为，设正方体棱长为，则，，，，即与平面所成角正弦值为． 21．（8分）在正方体中，求二面角平面角的正切值.【答案】【解析】解：如图，取的中点，连接，在正方体中，可知，所以，所以二面角的平面角为设，所以，所以，故答案为：． 22．（8分）如果直线l与平面所成的角为，且A，B是直线l上两点，线段在平面内的射影的长为3，求线段的长.【答案】【解析】解：当A或B在平面内时，如图，则，，，则，当A，B均不在平面内时，如图，过点A作AC∥DE，则AC=DE=3，，则，综上：线段的长为．23．（8分）在正方体中，，，分别是，，的中点.（1）证明：平面平面；（2）求直线与所成角的正切值.【答案】(1)证明见解析 (2)【解析】(1)证明：∵∥且EN平面MNE ,BC平面MNE ，∴BC∥平面MNE ，又∵∥且EM平面MNE , 平面MNE ,∴∥平面MNE，又∵,   ∴ 平面∥平面,(2)解：由（1）得∥,∴ 为直线MN与所成的角，设正方体的棱长为a，在△中，，，∴.24.（10分）已知矩形的两边，，平面，且，求二面角的正切值.【答案】【解析】解：如图所示，在平面内，过作的垂线，垂足为，连接，因为平面， 平面，所以，因为， ，故平面，因为平面，故，所以为的平面角，在直角三角形中， ，，故，故.