江苏省无锡市梁溪区2022-2023学年八年级上学期期中数学试卷(含答案)

2022-2023学年第一学期期中试卷

八年级数学

一．选择题（本大题共10小题，每题3分，共30分，在每小题所给出的四个选项中，只有一项是正确的，请用2B铅笔把答题卡上相应的选项标号涂黑。）

1．在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A． B． C． D．

2．如图，AC、BD相交于点O，∠1＝∠2，若用“SAS”说明△ACB≌△BDA，则还需要加上条件（　　）

A．AD＝BC B．BD＝AC C．∠D＝∠C D．OA＝AB

3．满足下列条件的△ABC不是直角三角形的是（　　）

A．BC＝1，AC＝2，AB＝ B．BC＝1，AC＝2，AB＝

C．BC：AC：AB＝3：4：5 D．∠A：∠B：∠C＝3：4：5

4．如图，数学课上，老师让学生尺规作图画∠MON的角平分线OB．小明的作法如图所示，连接BA、BC，你认为这种作法中判断△ABO≌△CBO的依据是（　　）

  A．SSS B．SAS C．ASA D．AAS

（第2题）               （第4题）                 （第7题）

5．已知一个等腰三角形有一个角为50°，则顶角是（　　）

A．50° B．80° C．50°或80° D．不能确定

6．下列说法正确的是（　　）

A．三个角对应相等的两个三角形全等 

B．面积相等的两个三角形全等 

C．全等三角形的面积相等 

D．两边和其中一边的对角对应相等的两个三角形全等

7．在正方形网格中，△ABC的位置如图所示，且顶点在格点上，在△ABC内部有E、F、G、H四个格点，到△ABC三个顶点距离相等的点是（　　）

A．点E B．点F C．点G D．点H

8．在直角三角形中，两条直角边长分别为5，12，则斜边上的中线长为（　　）

A．13 B．12 C．6.5 D．6

    （第9题）                        （第10题）

A．2 B．4 C． D．6

9．如图，正方形ABCD的边长为3，E在BC上，且BE＝2，P是BD边上一动点，则PE+PC的最小值为（　　）

A． B． C． D．

10．如图，△ABC中，∠ACB＝90°，BC＝3，AC＝4，点D是AB的中点，将△ACD沿CD翻折得到△ECD，连接AE，BE，则线段BE的长等于（　　）

A．  B． C． D．2

二．填空题（本大题共8小题，每题3分，第13、16题第一空1分，第二空2分，共24分，不需写出解答过程，请把答案直接填写在答题卡相应的位置上。）

11．正方形有　   　条对称轴．

12．已知等腰三角形的两边长分别为10和6，则三角形的周长是　   　．

13．如图，P是∠BAC平分线上一点，PE⊥AC于点E，PE＝1.5，AE＝2，则AP的长为　   　,点P到AB的距离是　   　.

  （第13题）          （第14题）        （第15题）     （第16题）

14．  如图，点B在AE上，∠C＝∠D，要证△ABC≌△ABD， 只需再补充一个条 件：　     　．

15．如图，△ABC中，∠ACB＝90°，AB＝6，分别以边AC、BC为直径向形外作两个半圆，则这两个半圆的面积的和为　   　． （结果中保留π）

16．如图，折叠长方形一边AD，点D落在BC边的点F处，已知BC＝10厘米，AB＝6厘米，则FC = 　   　,  EF = 　   　．

17．如图，已知四边形ABCD中，AB＝12cm，BC＝10cm，CD＝14cm，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以2cm/s的速度沿B﹣C运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为 　   　cm/s时，能够使△BPE与△CQP全等．

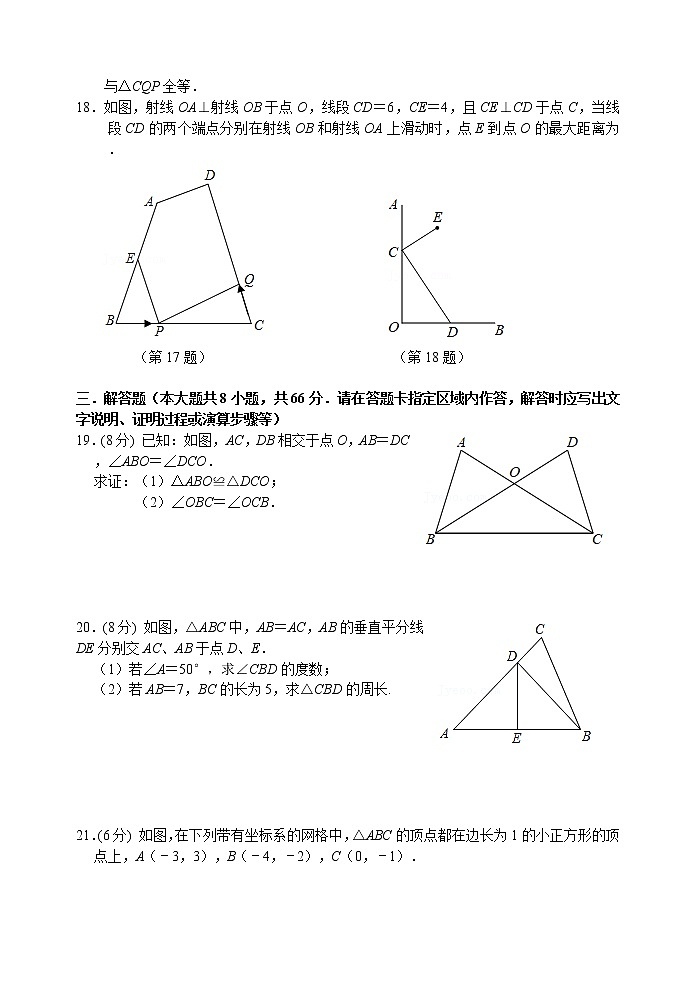
18．如图，射线OA⊥射线OB于点O，线段CD＝6，CE＝4，且CE⊥CD于点C，当线段CD的两个端点分别在射线OB和射线OA上滑动时，点E到点O的最大距离为 　   　．

   （第17题）                          （第18题）

三．解答题（本大题共8小题，共66分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤等）

19．(8分) 已知：如图，AC，DB相交于点O，AB＝DC，∠ABO＝∠DCO．

求证：（1）△ABO≌△DCO；

（2）∠OBC＝∠OCB．

20．(8分) 如图，△ABC中，AB＝AC，AB的垂直平分线DE分别交AC、AB于点D、E．

（1）若∠A＝50°，求∠CBD的度数；

（2）若AB＝7，BC的长为5，求△CBD的周长.

21．(6分) 如图，在下列带有坐标系的网格中，△ABC的顶点都在边长为1的小正方形的顶点上，A（﹣3，3），B（﹣4，﹣2），C（0，﹣1）．

（1）直接写出△ABC的面积为 　   　；

（2）画出△ABC关于y轴的对称的△DEC（点D与点A对应，点E与点B对应），点E的坐标为 　   　.

22．(6分) 已知在四边形ABCD中，∠A＝90°，AB＝3，AD＝4，BC＝12，CD＝13，求四边形ABCD的面积．

23．(8分) 如图，已知△ABC

（1）用直尺和圆规按下列要求作图：（保留作图痕迹）

作△ABC的角平分线AD；

作∠CBE＝∠ADC，BE交CA的延长线于E；

作AF⊥BE，垂足为F．

（2）图中BF与EF相等吗？证明你的结论．

24．(8分) 在七年级下册“证明”的一章的学习中，我们曾做过如下的实验：画∠AOB＝90°，并画∠AOB的平分线OC．

（1）把三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边分别与OA、OB相交于点E、F（如图①）．度量PE、PF的长度，这两条线段 　   　（填“相等”或“不相等”）．

（2）把三角尺绕点P旋转（如图②），PE与PF相等吗？请说明理由．

（3）探究：画∠AOB＝50°，并画∠AOB的平分线OC，在OC上任取一点P，作∠EPF＝130°．∠EPF的两边分别与OA、OB相交于E、F两点（如图③），PE与PF相等吗？请说明理由．

25．(10分) 新定义：若一个凸四边形的一条对角线把该四边形分成两个等腰三角形，那么称这个凸四边形为“等腰四边形”，这条对角线称为“界线”．

（1）如图1，四边形ABCD是“等腰四边形”，BD为“界线”，若∠BAD＝120°，∠BCD＝150°，则∠ABC＝　   　°；

（2）如图2，四边形ABCD中，AB＝AD，BC＝AB，∠A＝60°，∠D＝150°，试说明四边形ABCD是“等腰四边形”；

（3）若在“等腰四边形”ABCD中，AB＝BC＝CD，∠ABC＝90°，且BD为“界线”，请你画出满足条件的图形，并直接写出∠ADC的度数．

26．(12分) 如图1，△ABC中，CD⊥AB于D，且BD：AD：CD＝2：3：4，

（1）试说明△ABC是等腰三角形；

（2）已知S△ABC＝40cm2，如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止．设点M运动的时间为t（秒），

①若△DMN的边与BC平行，求t的值；

②若点E是边AC的中点，问在点M运动的过程中，△MDE能否成为等腰三角形？若能，请直接写出t的值；若不能，请说明理由．

2022-2023学年第一学期期中考试

参考答案及评分细则

一．选择题（共10小题）

1．A．2．B．3．D．4．A．5．C．6．C．7．B．8．C．9．D．10．A．

二．填空题（共8小题）

11．4.   12．22或26．13．2.5；1.5．14．∠CAB＝∠DAB （答案不唯一）

15．9π/2  16．2； 10/3.    17．2或．18.  8．

三．解答题（共8小题）

19．证明：（1）在△ABO和△DCO中，

证出：△ABO≌△DCO（AAS）；------------------------------------------4分

由（1）知，△ABO≌△DCO，∴OB＝OC;--------------------------------6分

∴∠OBC＝∠OCB．-------------------------------------------------------------8分

20．解：（1）∵AB=AC，∠A=50°，∴∠ABC=∠C=65°，----------1分
又∵DE垂直平分AB，∴DA=DB，------------------------------------------2分
∴∠ABD=∠A=50°，------------------------------------------------------------3分
∴∠CBD=15°；-------------------------------------------------------------------4分
（2）∵DE垂直平分AB，∴DA=DB，---------------------------------------5分
∴DB+DC=DA+DC=AC，---------------------------------------------------------6分
又∵AB=AC=7，BC=5，-----------------------------------------------------------7分
∴△CBD周长为12．--------------------------------------------------------------8分

21．（1）    （2分）；（2）画出△DEC  （4分）；4；（6分）

22．解：连接BD，

∵∠DAB＝90°，AB＝3，AD＝4，∴BD＝＝5，----------2分

∵BD2+BC2=52+122＝169,  CD2=132，∴BD2+BC2＝CD2

∴∠DBC＝90°，                         ----------------------------4分

∴四边形ABCD的面积=S△BCD —_S△ABD＝×5×12﹣×3×4＝24．-------------------6分

23．(1)作出角平分线---------2分，作出∠CBE＝∠ADC---------4分，

作出AF⊥BE，------6分;   （2）证出BF=EF  -----------8分.

24．（1）相等．----------------------------------------------------------------------1分

（2）PE＝PF，理由如下：如图②，作PM⊥OA于点M，PN⊥OB于点N，

∵∠AOB的平分线OC，PM⊥OA，PN⊥OB

∴PM＝PN，--------------------------------------------------------------------------3分

∵∠OMP＝∠ONP＝∠MON＝90°，且∠OMP+∠ONP+∠MON+∠MPN＝360°，

∴∠MPN＝90°，

∵∠EPF＝90°，

∴∠MPE＝∠NPF＝90°﹣∠EPN，-----------------------------------------4分

∵∠PME＝∠PNF＝90°，∴△PME≌△PNF（ASA），

∴PE＝PF，    -----------------------------------------------------------------5分

（3）PE＝PF，理由如下：--------------------------------------------------6分

如图③，在OF上取一点G，使OG＝OE，连接PG，

∵OC平分∠AOB，∴∠POG＝∠POE，

∵OP＝OP，∴△POG≌△POE（SAS），-----------------------------------7分

∴∠OGP＝∠OEP，PG＝PE，∴∠PGF+∠OEP＝∠PGF+∠OGP＝180°，

∴∠AOB＝50°，∠EPF＝130°，且∠AOB+∠EPF+∠PFG+∠OEP＝360°，

∴∠PFG+∠OEP＝180°，∴∠PGF＝∠PFG，∴PG＝PF，

∴PE＝PF．-------------------------------------------------------------------------8分

25．解：（1）45．-----------------------------------------------------------1分

（2）如图2，连接BD，∵AB＝AD，∠A＝60°，

∴△ABD是等边三角形，-----------------------------------------------2分

∴∠ADB＝60°，AB＝BD，

∵∠ADC＝150°，∴∠BDC＝∠ADC﹣∠ADB＝150°﹣60°＝90°，

∵∠C=45°

∴∠DBC＝∠C=45°

∴CD＝BD-------------------------------3分

∴AB＝AD，CD＝BD，

∴四边形ABCD是“等腰四边形”．-------------------4分

（3）如图3，

综上所述，∠ADC的度数为90°或135°或45°．--------------每画出一个图得1分，每写出一个角度得1分.

26.（1）证明：设BD＝2x，AD＝3x，CD＝4x，则AB＝5x，

在Rt△ACD中，AC＝＝5x，------------------------------------1分

∴AB＝AC，∴△ABC是等腰三角形；------------------------------------------2分

（2）解：S△ABC＝×5x×4x＝40cm2，而x＞0，∴x＝2cm，

则BD＝4cm，AD＝6cm，CD＝8cm，AC＝10cm．

①当MN∥BC时，AM＝AN，

即10﹣t＝t，∴t＝5；----------------------------------------------------------------4分

当DN∥BC时，AD＝AN，得：t＝6；-------------------------------------------6分

∴若△DMN的边与BC平行时，t值为5或6．

②符合要求的t值为9或10或．-----------------------每写出一个值得2分