2022-2023学年云南省楚雄州楚雄市七年级（上）期中数学试卷（含解析）

2022-2023学年云南省楚雄州楚雄市七年级（上）期中数学试卷

一、选择题（本大题共12小题，共36分。）

1.    在，，，中，负数的个数是(    )

A.  B.  C.  D.

2.    北京奥运会主会场“鸟巢”的座席数是个，用科学记数法表示为(    )

A.  B.  C.  D.

3.    下列结果正确的是(    )

A.  B.
C.  D.

4.    某城市一月份某一天的天气预报中，最低气温为，最高气温为，这一天这个城市的温差为(    )

A.  B.  C.  D.

5.    下列方程是一元一次方程的是(    )

A.  B.  C.  D.

6.    下列各组中，不是同类项的是(    )

A. 与 B. 与 C. 与 D. 与

7.    下列说法正确的是(    )

A. 是单项式 B. 的系数是
C. 是单项式 D. 的次数是

8.    下列各对数中，数值相等的是(    )

A. 与 B. 与
C. 与 D. 与

9.    化简的最后结果是(    )

A.  B.  C.  D.

10. 如果，，则的值为(    )

A.  B.
C. 和 D. ，，，

11. 若，则的值是(    )

A.  B.  C.  D.

12. 某商品的标价为元，折销售仍赚元，则商品进价为元．(    )

A.  B.  C.  D.

二、填空题（本大题共6小题，共18分。）

13. 的相反数是______．
14. 如果向东走米记为米，那么向西走米记为______ 米．
15. 根据要求，用四舍五入法取下列各数的近似值：______精确到．
16. 与是同类项，则______．
17. 已知方程的解是，则的值为______ ．
18. 如图是用棋子摆成的“上”字，按照以上规律继续摆下去，那么通过观察，第个“上”字需用棋子的枚数是______枚．
     

三、解答题（本大题共6小题，共46分。）

19. 计算：
    ；
     
20. 画一条数轴，并在数轴上表示：，，，，，并把这些数由小到大用“”号连接起来．
21. 先化简，后求值．
    ；
    ，其中，．
22. 解方程
    
    ．
23. 小明买苹果和梨共千克，用去元，其中苹果每千克元，梨每千克元，问苹果和梨各买了多少千克？
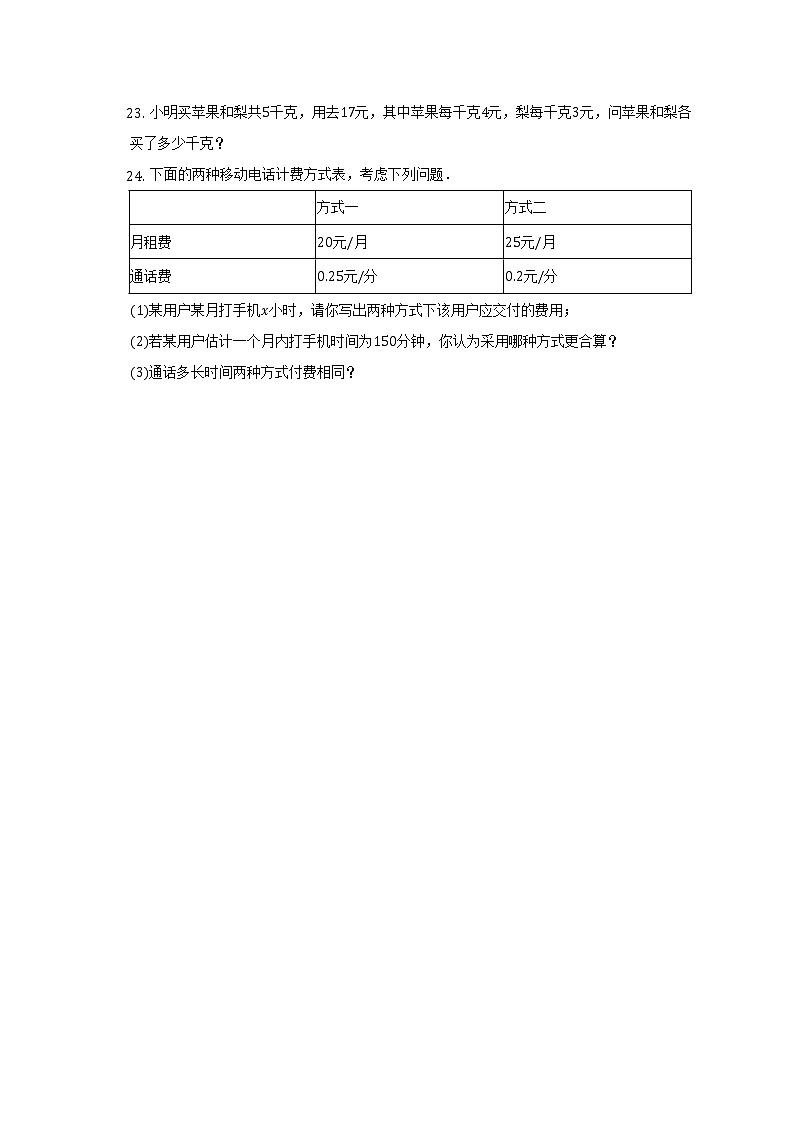
24. 下面的两种移动电话计费方式表，考虑下列问题．

某用户某月打手机小时，请你写出两种方式下该用户应交付的费用；
若某用户估计一个月内打手机时间为分钟，你认为采用哪种方式更合算？
通话多长时间两种方式付费相同？

答案和解析

1.【答案】 

【解析】解：在，，，中，负数有，，，共有个，
故选：．
根据正数与负数的特征进行判断即可．
本题考查正数与负数，理解正数与负数的特征是正确判断的前提．
 

2.【答案】 

【解析】解：，
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正数；当原数的绝对值时，是负数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
 

3.【答案】 

【解析】解：，故本选项不合题意；
B.，故本选项不合题意；
C.，故本选项不合题意；
D.，故本选项符合题意．
故选：．
合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变．
本题考查了合并同类项，掌握合并同类项法则是解答本题的关键．
 

4.【答案】 

【解析】解：


故选：．
根据题意：求这一天的温差是多少，即求最高气温与最低气温二者之差，列式为，解答即可．
本题考查有理数减法，正、负数的简单运算，正确列式是解题的关键．
 

5.【答案】 

【解析】解：、是二元一次方程，故错误；
B、是一元二次方程，故错误；
C、是分式方程，不是整式方程，故错误；
D、即，是一元一次方程，正确．
故选D．
只含有一个未知数元，并且未知数的指数是次的方程叫做一元一次方程，它的一般形式是是常数且，高于一次的项系数是．
本题主要考查了一元一次方程的定义，只含有一个未知数，未知数的指数是，一次项系数不是，这是这类题目考查的重点．
 

6.【答案】 

【解析】解：与，两个单项式均含有字母、，且、的指数分别相同，是同类项，故本选项不合题意；
B.与，两个单项式均含有字母、，且、的指数分别相同，是同类项，故本选项不合题意；
C.与，两个单项式均含有字母、，且、的指数分别相同，是同类项，故本选项不合题意；
D.与，两个单项式均含有字母、，但、的指数不相同，不是同类项，故本选项符合题意．
故选：．
首先确定各选项里的两个单项式的字母部分是否相同；接下来看相同字母的指数是否相同，即可作出判断．
本题考查了同类项的定义：所含字母相同，并且相同字母的指数也相同的项叫同类项．
 

7.【答案】 

【解析】解：是单项式，故此选项符合题意；
B.的系数是，故此选项不合题意；
C.不是单项式，故此选项不合题意；
D.的次数是，故此选项不合题意．
故选：．
直接利用单项式的定义以及单项式的系数确定方法、多项式的次数确定方法分别判断得出答案．
此题主要考查了多项式、单项式，正确掌握相关定义是解题关键．
 

8.【答案】 

【解析】解：、，，故A错误；
B、，，故B错误；
C、，，故C正确；
D、，，故 D错误；
故选：．
根据乘方的意义，可得答案．
本题考查了有理数的乘方，根据乘方的意义得出每组数据的值是解题关键，注意底数的底数是，的底数是．
 

9.【答案】 

【解析】解：原式
．
故选：．
原式去括号合并即可得到结果．
此题考查了整式的加减，熟练掌握运算法则是解本题的关键．
 

10.【答案】 

【解析】

【分析】
此题考查了绝对值的性质，要求掌握绝对值的性质及其定义，并能熟练运用到实际当中．规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；的绝对值是由绝对值的性质与，，得出，，从而得出有四种情况，求得的值．
【解答】
解：，，，，
当，时，；
当，时，；
当，时，；
当，时，．
故选D．  

11.【答案】 

【解析】解：，
，，
解得：，，
故．
故选：．
利用非负数的性质得出、的值，代入计算得出答案．
本题考查非负数的性质，掌握非负数的意义和性质是正确解答的前提．
 

12.【答案】 

【解析】解：设商品的进价为每件元，售价为每件元，
由题意，得，
解得．
故选：．
设商品进价为每件元，则售价为每件元，由利润售价进价建立方程求出其解即可．
本题考查了销售问题的数量关系利润售价进价的运用，列一元一次方程解实际问题的运用，解答时根据销售问题的数量关系建立方程是关键．本题考查了销售问题的数量关系利润售价进价的运用，列一元一次方程解实际问题的运用，解答时根据销售问题的数量关系建立方程是关键．
 

13.【答案】 

【解析】解：的相反数是：．
故答案为：．
直接利用相反数的概念：只有符号不同的两个数叫做互为相反数，进而得出答案．
此题主要考查了相反数，正确掌握相反数的定义是解题关键．
 

14.【答案】 

【解析】解：“正”和“负”相对，
向东走米记为米，
向西走米记为米．
在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．
解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．
 

15.【答案】 

【解析】解：用四舍五入法取下列各数的近似值：精确到，
故答案为：．
对百分位数字四舍五入即可．
本题主要考查近似数，近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．
 

16.【答案】 

【解析】解：与是同类项，
，，
．
故答案为：．
根据同类项的定义可得、的值，再代入计算即可．
本题考查了同类项的定义：所含字母相同，并且相同字母的指数也相同的项叫同类项．
 

17.【答案】 

【解析】解：方程的解是，
，
解得：．
故答案为：．
直接把的值代入方程求出答案．
此题主要考查了一元一次方程的解，正确解方程是解题关键．
 

18.【答案】 

【解析】解：第个“上”字中的棋子个数是；
第个“上”字中的棋子个数是；
第个“上”字中的棋子个数是；

所以，第个“上”字中的棋子个数是，
故答案为：
由图可得，第个“上”字中的棋子个数是；第个“上”字中的棋子个数是；第个“上”字中的棋子个数是；进一步发现规律：第个“上”字中的棋子个数是；由此求得问题答案．
本题考查了图形的变化规律，关键是通过归纳与总结，得到其中的规律，利用规律解决问题．
 

19.【答案】解：


；



． 

【解析】利用乘法的分配律进行求解即可；
先算绝对值，乘方，再算除法，最后算加法即可．
本题主要考查有理数的混合运算，解答的关键是对相应的运算法则的掌握．
 

20.【答案】解：在数轴上表示出来如图所示：

根据这些点在数轴上的排列顺序，从左至右分别用“”连接为：
． 

【解析】先分别把各数在数轴上找出对应的点，再按从左到右的顺序排列即可．
此题考查了数轴，由于引进了数轴，我们把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．
 

21.【答案】解：原式
．
原式
，
当，时，
原式

． 

【解析】根据整式的加减运算法则即可求出答案．
根据整式的加减运算法则进行化简，然后将与的值代入原式即可求出答案．
本题考查整式的加减运算，解题的关键是熟练运用整式的加减运算法则，本题属于基础题型．
 

22.【答案】解：去括号得：，
移项合并得：，
解得：；
去分母得：，
移项合并得：，
解得：． 

【解析】方程去括号，移项合并，把系数化为，即可求出解；
方程去分母，去括号，移项合并，把系数化为，即可求出解．
此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．
 

23.【答案】解：设苹果买了千克，梨买了千克．
由题意得：，
解得：．
．
答：苹果买了千克，梨买了千克． 

【解析】等量关系为：，把相关数值代入即可求解．
解决本题的关键是得到两种水果总价的等量关系，比较简单．
 

24.【答案】解：设通话时间为小时时方式一和方式二对应下的总话费分别为和，
由总电话费月租费通话费得：
，
；
由中的解析式，将分别代入和得：
，
，
，
采取方式二更合算；
由得：，
通话小时两种方式付费相同． 

【解析】根据公式：总电话费月租费通话费，分别写出方式一和方式二的总话费和通话时间之间的函数关系，
结合，利用两函数可计算两种方式下对应的总话费，从而比较哪种更合算；
结合列出方程，即可解得答案．
本题考查一次函数及一元一次方程的应用，解题的关键是读懂题意，列出函数关系式．