山东省淄博市高青县2022-2023学年七年级上学期期中数学试题(含答案)

2022—2023学年度第一学期期中复习训练题

七年级数学

一、选择题（本题有10小题，每小题4分，共40分，每小数只有一个选项是正确的，不选、多选、错选，均不得分）

1．北京2022年冬奥会会徽（冬梦），是第24届冬季奥林匹克运动会使用的标志，主要由会徽图形、文字标志、奥林匹克五环标志组成，组成会徽的四个图案中是轴对称图形的是（    ）

A．    B．    C．    D．

2．如图，在中，边上的高是（    ）

A．线段    B．线段    C．线段    D．线段

3．如图，直线，垂足为O，线段，，以点A为圆心，的长为半径画弧，交直线于点C．则的长为（    ）

A．5    B．4    C．3    D．2

4．如图，把沿翻折，叠合后的图形如图，若，，则的度数是（    ）

A．    B．    C．    D．

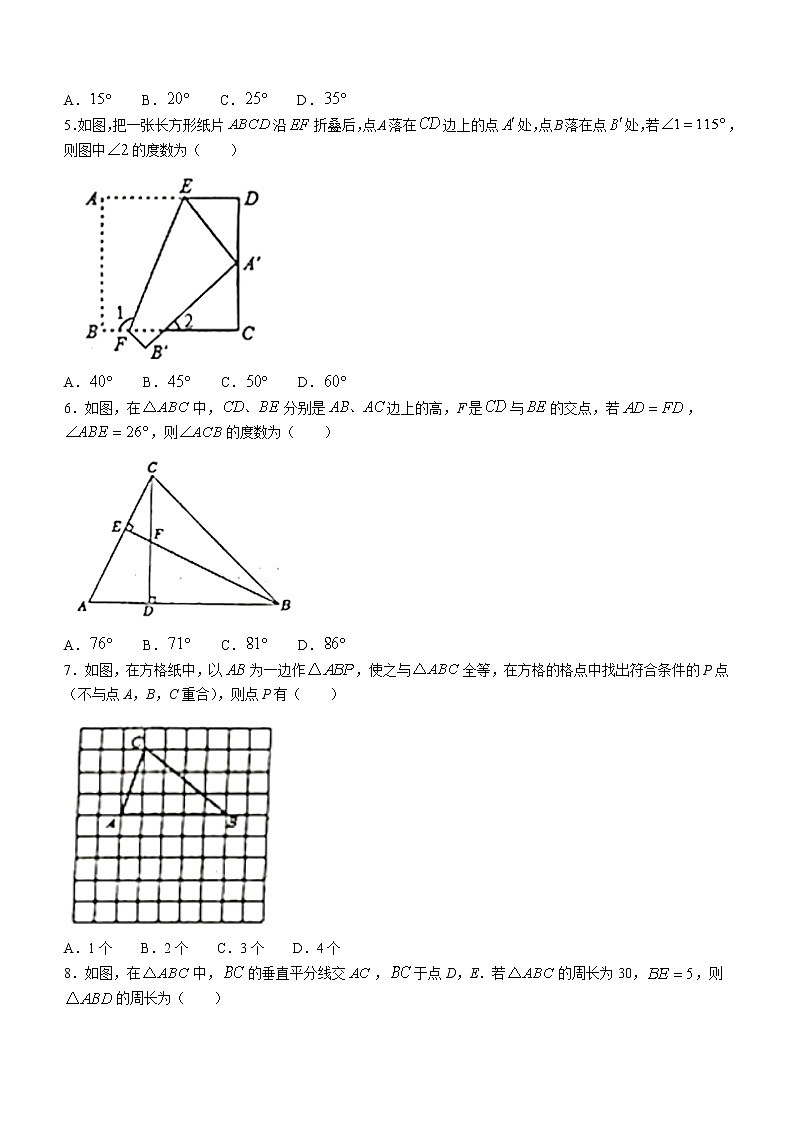
5．如图，把一张长方形纸片沿折叠后，点A落在边上的点处，点B落在点处，若，则图中的度数为（    ）

A．    B．    C．    D．

6．如图，在中，分别是边上的高，F是与的交点，若，，则的度数为（    ）

A．    B．    C．    D．

7．如图，在方格纸中，以为一边作，使之与全等，在方格的格点中找出符合条件的P点（不与点A，B，C重合），则点P有（    ）

A．1个    B．2个    C．3个    D．4个

8．如图，在中，的垂直平分线交，于点D，E．若的周长为30，，则的周长为（    ）

A．10    B．15    C．20    D．25

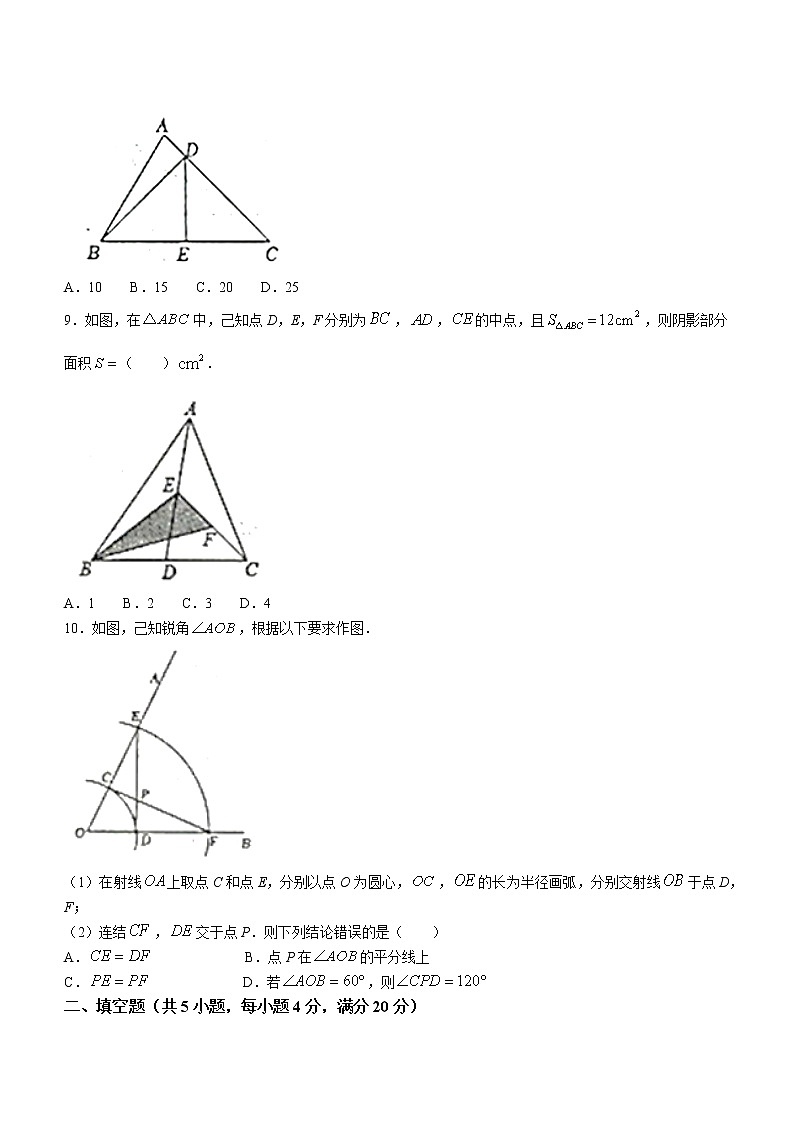
9．如图，在中，己知点D，E，F分别为，，的中点，且，则阴影部分面积（    ）．

A．1    B．2    C．3    D．4

10．如图，己知锐角，根据以下要求作图．

（1）在射线上取点C和点E，分别以点O为圆心，，的长为半径画弧，分别交射线于点D，F；

（2）连结，交于点P．则下列结论错误的是（    ）

A．             B．点P在的平分线上

C．             D．若，则

二、填空题（共5小题，每小题4分，满分20分）

11．如图，若，相交于点E，若，，则的度数是___________．

12．如图，在中，，平分，于点D，如果，，则等于_______________．

13．如图，是的中线，，，和的周长的差是____________．

14．如图，在中，，，．现将按如图那样折叠，使点A与点B重合，折痕为，则的长为____________．

15．如图，“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒，组成，两根棒在O点相连并可绕O转动，C点固定，，点D、E可在槽中滑动．若，则的度数是___________．

三、解答题（共8小题，共90分）

16．如图，在中，点D在边上，，，．求证：．

17．如图，已知中，，，是的角平分线，于E点．

（1）求的度数；

（2），，，求．

18．如图，用10块高度相同长方体小木块垒了两堵与地面垂直的木墙、，，，两木墙之间刚好可以放进一个等腰直角三角板（，）．点C在上，点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．

19．如图，在中，于点D，，，．

（1）求的长；

（2）求的长；

（3）求的度数．

20．如图：在中，D是边的中点，E是边的中点，连接，．

（1）若，，，求证：；

（2）若，，，求的面积．

21．如图，在中，是的高．

（1）如图1，是的平分线，若，，求的度数．

（2）如图2，延长到点F，和的平分线交于点G、求的度数．

22．如图，在中，，D为延长线上一点，且交于点F．

（1）求证：是等腰三角形；

（2）若，，F为中点，则__________．

23．如图，在中，的垂直平分线分别交线段，于点M，P，的垂直平分线分别交线段，于点N，Q．

（1）如图，当时，求的度数；

（2）当时，求的度数．

2022—2023学年度第一学期期中复习训练题

七年级数学参考答案

一、选择题：本题共10小题，每小题4分，共40分

二、填空题：每小题4分，共20分

三、解答题：

16．证明：∵，

∴，

在和中，

，

∴，

∴．

17．解：（1）∵，，

∴，

∵是的角平分线，

∴；

（2）如图，过D作于F，

∵是的角平分线，，

∴，

又∵，

∴．

18．解：由总意得：，，，，

∴，

∴，，

∴，

在和中，

，

∴；

由题意得：，

∴，

答：两堵水墙之间的距离为．

19．解：（1）∵．

∴．

（2）在中，，

∴，

则．

（3）∵，即，

∴为直角三角形，．

20．（1）证明：∵D是边的中点，E是边的中点，，

∴，

∵，

∴，

∴是直角三角形，

∴；

（2）解：∵E是边的中点，，

∴．

在中，∵，

∴，

∴，

∴的面积．

21．解：（1）∵

∴，

∵是的角平分线，

∴，

∵是的高，

∴，

∵，

∴，

∴；

（2）∵和的角平分线交于点G，

∴，，

∵，，

∴，

即，

∵是的高，

∴，

∴．

22．（1）证明：∵，

∴,

∵，

∴，

∴，，

∴，

∵，

∴，

∴，

∴是等腰三角形；

（2）过点A作，垂足为G，

∵，，

∴，

∵F为中点，

∴，

在中，，

∴，

∵，，

∴，

∴．

∵，，

∴，

∴，

∴，

23．解：（1）∵、分别是的垂直平分线，

∴，，

∵，

∴，

∵，，

∴，，

∴

（2）∵分别是的垂直平分线，

∴，，

∴，，

∴，

当P点在Q点右侧时，

∵，，

∴，

∵，

∴．

当P点在Q点左侧时，

∵，，

∴，

∵，

∴．

综上或．