北师大版 数学八年级上册 勾股定理回顾与思考 优质课件

这是一份北师大版 数学八年级上册 勾股定理回顾与思考 优质课件，共18页。PPT课件主要包含了第二环节自主学习，第三环节合作探究，合作探究，∴AD和AB垂直，AB25，x24，拓展提升，谈谈你的收获等内容，欢迎下载使用。
勾股定理，我们把它称为世界第一定理．它的重要性，通过这一章的学习已深有体验，首先，勾股定理是数形结合的最典型的代表；其次，了解勾股定理历史的同学知道，正是由于勾股定理得发现，导致无理数的发现，引发了数学的第一次危机，这一点，我们将在《实数》一章里讲到。勾股定理是我们数学史的奇迹，我们已经比较完整地研究了这个先人给我们留下来的宝贵的财富，这节课，我们将通过回顾与思考中的几个问题更进一步了解勾股定理的历史，勾股定理的应用．
本章知识要点回顾：（先学生自主学习、独立思考完成，再小组代表展示）1．勾股定理：直角三角形两直角边的平方和等于斜边的平方，如果用 和 分别表示直角三角形的直角边和斜边，那么2．勾股定理的逆定理： 在△ABC中，若三边满足 ，则△ABC为3． 勾股数：满足 的三个 ，称为勾股数．4．几何体上的最短路程是将立体图形的 展开，转化为 上的路程 问题，再利用平面上：两点之间， 解决最短线路问题． 立体图形 → 平面图形 → 直角三角形问题5．本章的知识结构图． 三边的关系­­­------勾股定理→历史、应用直角三角形 直角三角形的判别------勾股定理逆定理→应用
探究一：利用勾股定理求边长已知直角三角形的两边长分别为3、4，求第三边长的平方．解：（1）当两直角边为3和4时，第三边长的平方为25； （2）当斜边为4，一直角边为3时，第三边长的平方为7．点拨： 学生习惯了“勾三股四弦五”的说法，即意味着两直角边3和4时，斜边长为5．但这一理解的前提是3、4为直角边而本题中并未加以任何说明，因而所求的第三边可能为斜边，但也可能为直角边 注意数学中的分情况讨论思想！
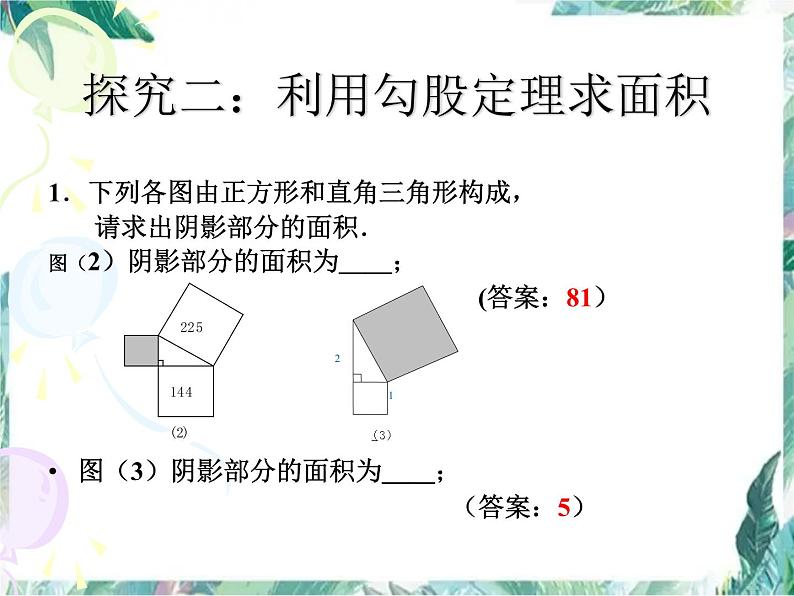
探究二：利用勾股定理求面积
1．下列各图由正方形和直角三角形构成， 请求出阴影部分的面积．图（2）阴影部分的面积为＿＿； (答案：81）图（3）阴影部分的面积为＿＿； （答案：5）
2． 已知Rt△ABC中， ，若 ， 求Rt△ABC的面积．
探究二：利用勾股定理求图形面积
点拨：灵活应用公式及数学中的整体考虑思想！
探究三：利用勾股定理逆定理判定△ABC的形状或求角度
1. 在△ABC中， 的对边分别为 且 ，则（ ）. （A） 为直角 （B） 为直角 （C） 为直角 （D）不是直角三角形 解：∵ ∴ ∴ 故选（A）
（2）李叔叔量得AD长是30厘米，AB长是40厘米，BD长是50厘米，AD边垂直于AB边吗？为什么？
2 李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB，但他随身只带了卷尺，（1）你能替他想办法完成任务吗？
探究三：利用勾股定理逆定理判定△ABC的形状或求角度
学以致用，实践出真知
1．如图，台阶A处的蚂蚁要爬到B处搬运食物，它怎么走最近？并求出最近距离。
探究四：勾股定理及逆定理的综合应用：
上下靠右行礼让讲秩序
（学会数学中的转化思想！）
中国古代人民的聪明才智真是令人赞叹 !
2．在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？
我们祖先的历史趣题：
解：设水池的水深AC为x尺，则这根芦苇长为AD=AB=（x+1）尺，
在直角三角形ABC中，BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1，
∴ x=12， x+1=13
答：水池的水深12尺，这根芦苇长13尺。
（学会数学中的方程思想！）
向国旗敬礼时突发奇想：
3 周一升旗时，小明穿着校服唱着国歌向国旗行注目礼时，他看到旗杆上的绳子垂到了地面，并多出了一段，很想知道旗杆的高度，你能帮小明想个办法吗?请你与同伴交流设计方案? （知识迁移,学以致用， 实践出真知）
第四环节：当堂检测------ （限时检测，评价加分， 讨论纠错，点拨提升）
检测时间：10分钟 批改人签字： 我的得分：
1. 已知在Rt△ABC中，∠C=90°，若a=8，c=17，则b=_______.（3分）2．放学以后，小红和小颖从学校分手，分别沿东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖20分钟到家，小红和小颖家的直线距离为（ ） （3分） A．600米 B. 800米 C. 1000米 D. 不能确定3．如图，学校有一块长方形花圃，有极少数人为了避开拐角走 “捷径”，在花圃内走出了一条“路”.他们仅仅少走了 步路， 却踩伤了花草．（假设2步为1米） （3分） 4 八年级某数学课外活动小组的同学测量学校旗杆的高度时，发现 升旗的绳子垂到地面要多1米，当他们把绳子的下端拉开5米后， 发现下端刚好接触地面。请你帮助他们求出旗杆的高度。（3分） （反思） 你的解答过程中用了初中数学里的_____定理、______公式、______思想。（3分）
我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）．图2由“弦图”变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3=10，则S2的值是 ．
1、本章知识要点及在学习中用到了哪些数学思想方法？ 2、你在学习过程中是否积极参与？是否与同伴进行了有效的合作交流？ 3 、 是否体会到勾股定理及其逆定理的广泛应用及它们的悠久历史？
1 《一课一练》 第一章 勾股定理 回顾与思考2．思考、更正、讨论当堂检测题