初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆备课课件ppt

这是一份初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆备课课件ppt，共19页。PPT课件主要包含了教学目标，教学重难点，圆的动态定义，特殊的圆，同心圆，圆心相同半径不等，半径相等圆心不同，圆的静态定义，与圆有关的概念，直径是特殊的弦等内容，欢迎下载使用。
弦：直径：圆弧（弧）：半圆：优弧、劣弧：等圆：等弧：
在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。
圆心为O、半径为r的圆可以看成是平面内所有到定点O的距离等定长r的点的集合。
连接圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
圆上任意两点间的部分叫做圆弧，简称弧。
圆的任意一条直径的两个端点把圆分成两条弧，每条弧 都叫做半圆。
能够重合的两个圆叫做等圆。
大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧。
在同圆或等圆中，能够互相重合的弧叫做等弧。
判断下列说法的正误，并说明理由或举反例。
(1)圆心相同，半径相等的两个圆是同心圆;（ ）(2)半径相等的两个圆是等圆。（ ）
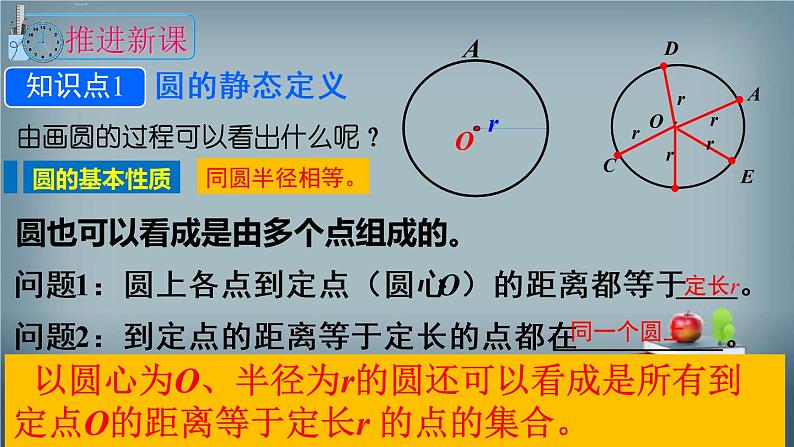
问题1：圆上各点到定点（圆心 O）的距离都等于 。问题2：到定点的距离等于定长的点都在 。
由画圆的过程可以看出什么呢？
以圆心为O、半径为r的圆还可以看成是所有到定点O的距离等于定长r 的点的集合。
圆也可以看成是由多个点组成的。
例1 矩形ABCD的对角线AC、BD相交于O。求证：A、B、C、D在以O为圆心的同一圆上。
(1)弦是直径。（ ）(2)直径是弦。（ ）(3)半径是弦。（ ）(4)直径是圆中最长的弦。（ ）
(1)半圆是弧。（ ）(2)圆的任意一条弦把圆分成优弧和劣弧两部分。（ ）
能够重合的两个圆叫做等圆；
(1)长度相等的弧是等弧。（ ）(2)等弧的长度相等。（ ）
结论：等弧仅仅存在于同圆或者等圆中。
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图，如果AB和CD的拉直长度都是10cm，平移并调整小圆的位置，是否能使这两条弧完全重合？
想一想：长度相等的弧是等弧吗？
2、一个圆的最长的弦长是10cm，则此圆的半径是 cm。
1、如图，在5×5正方形网格中，一条圆弧经过A、B、C三点，那么这条圆弧所在圆的圆心是（ ）A、点P B、点Q C、点R D、点M
3、如图，MN是的弦，∠MON=120°，那么∠M= 。
2.所对的圆心角相等或长度相等
1、以已知点O为圆心，可以画 个圆；以已知线段AB的长为半径，可以画 个圆.2、已知⊙O中最长的弦为10cm，则⊙O的半径为 cm.3、如下图所示，在⊙O中，AB为直径，P点为OB上一点（不同于O、B），CD、EF是⊙O中过点P的两条弦，则图中有 条直径， 条非直径的弦，以A为一个端点的劣弧有 条.
4、下列判断中，不正确的个数是（ ）.①直径是弦;②弧包括优弧和劣弧；③等弧是长度相等的弧；④经过圆内一定点可以作无数条直径.A.1个 B.2个 C.3个 D.4个5、设AB=3cm，画图说明具有下列性质的点的集合是怎样的图形.(1)和点A的距离等于2cm的点的集合； (2)和点B的距离等于2cm的点的集合；(3)和点A，B的距离都等于2cm的点的集合；(4)和点A，B的距离都小于2cm的点的集合.
6.思考：车轮为什么做成圆形的？如果车轮不是圆的（比如椭圆或正方形），坐车的人会是什么感觉？
1、以已知点O为圆心，已知线段a为半径作圆，可以作（ ）。A.1个 B.2个 C.3个 D.无数个2、点P到圆上各点的最大距离是8cm，最小距离是6cm，则圆的半径是（ ）. A.7 cm B.1 cm C.7 cm或1 cm D.无法确定3、如图，⊙O的半径为3 cm，A为⊙O上一定点，P在⊙O上沿圆周运动（不与A重合），则弦AP的长度为整数值的有 个，这样的弦共有 条.
要画一个确定的圆，关键是确定圆心和半径