初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.4 圆周角教案

24.1.4  圆周角教学设计

教学目标：
知识技能：

1.理解圆周角的概念，会叙述并证明圆周角定理.

2.理解掌握圆周角定理及其推理.

3.能应用圆周角定理及推论解决简单的几何问题.

情感目标:

1.通过圆周角定理的证明及推论的得到向学生渗透由“特殊到一般”，再由“一般到特殊”的研究问题方法，体会分类讨论、化归的思想方法。变与不变的思想.

2.激发学生探究数学的兴趣和热情，培养学生积极追求真理的精神.

能力目标：

培养学生分析问题和解决问题的能力，逻辑推理能力，进一步提升学生的逻辑推理素养.

教学重点：圆周角定理．

教学难点：圆周角定理的证明．

教学过程:

知识回顾

说一说下列图形名称，写的时候应该注意什么

写的时候应该注意按顺时针或逆时针顺序

情境导入

观察下列图形与圆的位置关系

多边形的顶点都在圆上

新知探究

定义：如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做这个多边形的外接圆.

圆内接四边形对角互补

几何语言：

∵四边形ABCD内接于⊙O

∴∠A+∠C=180,∠B+∠D=180

结论：圆内接四边形的任何一个外角都等于它的内对角.

求证：圆内接四边形的任何一个外角都等于它的内对角.已知：如图，四边形 ABCD是⊙O的内接四边形.求证：∠DCE=∠A.

当堂检测

1.如图，点A、B、C在圆O上，BC∥OA，连接BO并延长，交圆O于点D，连接AC，DC，若∠A＝28°，则∠D的大小为 　   　．

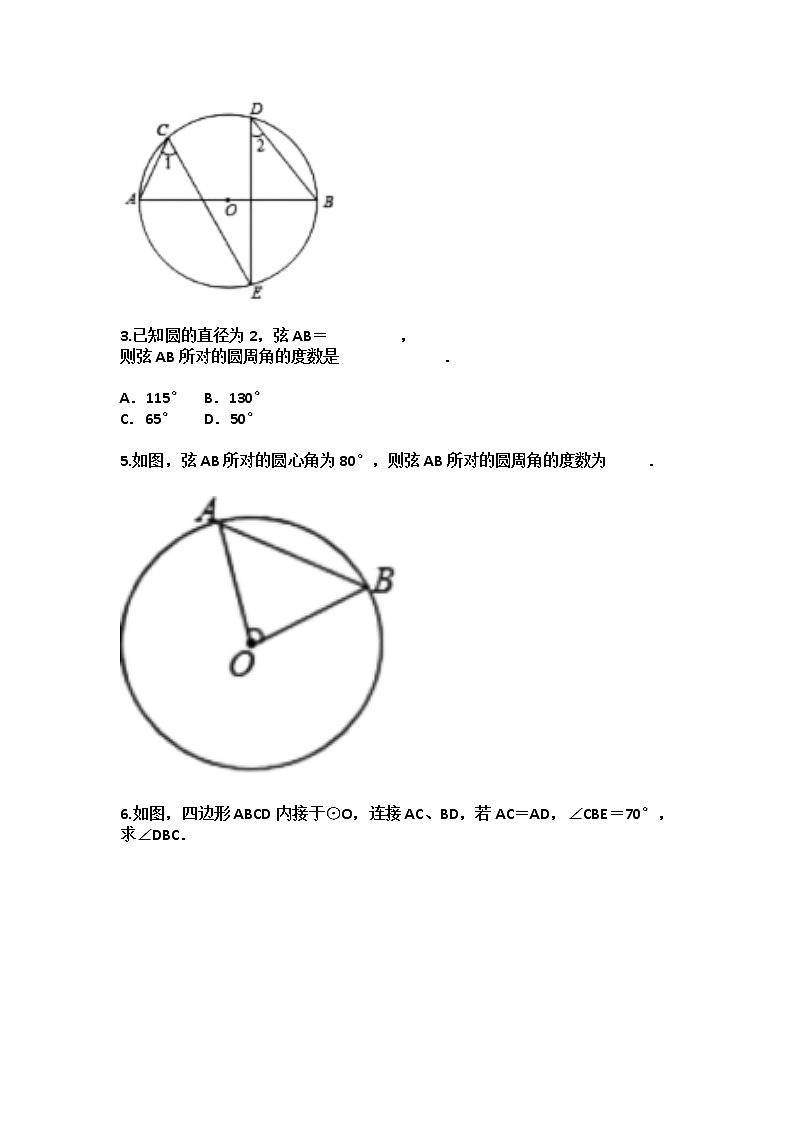
2.如图，AB是⊙O的直径，点C，D，E都在⊙O上，∠1＝54°，则∠2＝　　°．

3.已知圆的直径为2，弦AB＝         ，

则弦AB所对的圆周角的度数是 　　        ．

A．115° B．130° 

C．65° D．50°

5.如图，弦AB所对的圆心角为80°，则弦AB所对的圆周角的度数为 　　．

6.如图，四边形ABCD内接于⊙O，连接AC、BD，若AC＝AD，∠CBE＝70°，求∠DBC．

课堂小结

圆周角定理：

定理一条弧所对的圆周角等于它所对的圆心角的一半.

推论

同弧或等弧所对的圆周角相等；

在同圆或等圆中，相等的圆周角所对的弧相等.

半圆（或直径）所对的圆周角是90°；

90°的圆周角所对的弦是直径.

圆内接四边形的性质：圆内接四边形对角互补