人教版八年级上册14.3.2 公式法示范课课件ppt

这是一份人教版八年级上册14.3.2 公式法示范课课件ppt，共21页。PPT课件主要包含了教学目标，教学重难点，解1原式，2原式，整体思想，例2分解因式，多次因式分解，利用因式分解进行证明等内容，欢迎下载使用。
1、能识别平方差公式的结构特征。 2、能较熟练地应用平方差公式分解因式。 3、在合作学习过程中增强与他人的合作意识，提升学习信心。
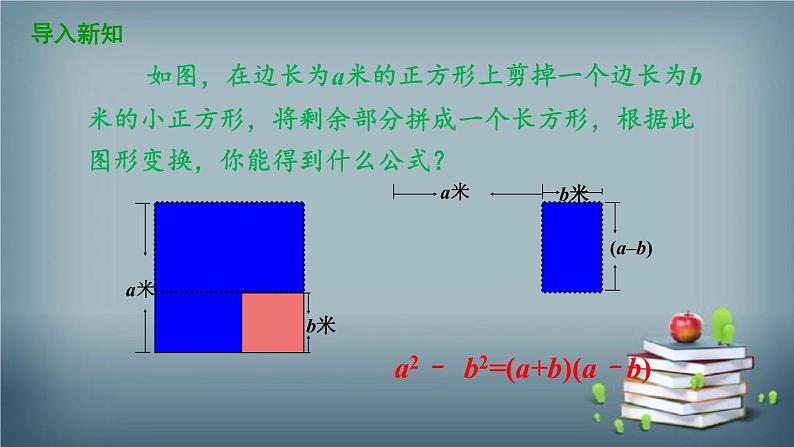
如图，在边长为a米的正方形上剪掉一个边长为b米的小正方形，将剩余部分拼成一个长方形，根据此图形变换，你能得到什么公式？
a2– b2=(a+b)(a–b)
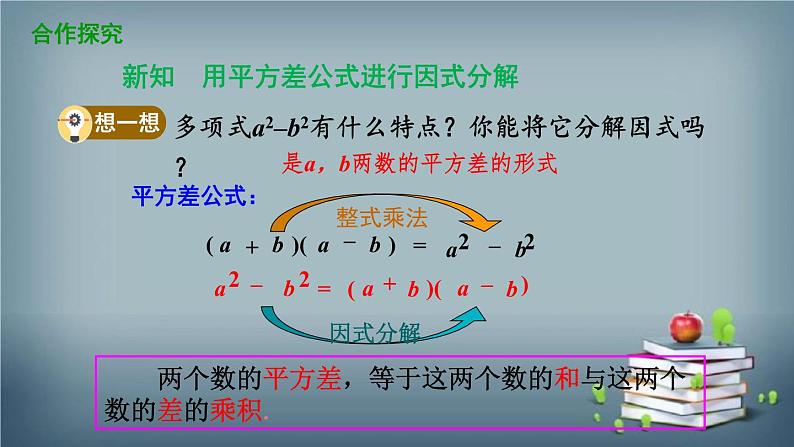
新知 用平方差公式进行因式分解
多项式a2–b2有什么特点？你能将它分解因式吗？
是a，b两数的平方差的形式
两个数的平方差，等于这两个数的和与这两个数的差的乘积.
辨一辨：下列多项式能否用平方差公式来分解因式，为什么？
两数是平方，减号在中央．
(x+5y)(x–5y)
a2 – b2 =
利用平方差公式分解因式的应用
公式中的a、b无论表示数、单项式、还是多项式，只要被分解的多项式能转化成平方差的形式，就能用平方差公式因式分解.
解：(1)原式＝(x2)2–(y2)2
＝(x2+y2)(x2–y2)
＝(x2+y2)(x+y)(x–y);
(2)原式＝ab(a2–1)
＝ab(a+1)(a–1).
分解因式前应先分析多项式的特点，一般先提公因式，再套用公式．必须进行到每一个多项式都不能再分解因式为止．
例3 已知x2–y2＝–2，x＋y＝1，求x–y，x，y的值．
解：∵x2–y2＝(x＋y)(x–y)＝–2，
联立①②组成二元一次方程组，
利用因式分解求整式的值
例4 计算下列各题：(1)1012–992； (2)53.52×4–46.52×4.
解：(1)原式＝(101＋99)(101–99)＝400；
(2)原式＝4×(53.52–46.52)
＝ 4× (53.5＋46.5)(53.5–46.5)
＝4×100×7=2800.
方法总结：较为复杂的有理数运算，可以运用因式分解对其进行变形，使运算得以简化.
利用因式分解进行简便运算
例5 求证：当n为整数时，多项式(2n+1)2–(2n–1)2一定能被8整除．
即多项式(2n+1)2–(2n–1)2一定能被8整除．
证明：原式=(2n+1+2n–1)(2n+1–2n+1)=4n•2=8n，
方法总结：解决整除的基本思路就是将代数式化为整式乘积的形式，然后分析能被哪些数或式子整除．
1.下列多项式中能用平方差公式分解因式的是(　　)A．a2＋(–b)2 B．5m2–20mnC．–x2–y2 D．–x2＋9
2. 将多项式x–x3因式分解正确的是(　　)A．x(x2–1) B．x(1–x2)C．x(x+1)(x–1) D．x(1+x)(1–x)
3.若a+b=3，a–b=7，则b2–a2的值为(　　)
A．–21 B．21 C．–10 D．10
4.把下列各式分解因式：(1)16a2–9b2=_________________; (2)(a+b)2–(a–b)2=_________________; (3) 因式分解：2x2–8=_________________; (4) –a4+16=_________________.
(4a+3b)(4a–3b)
(4+a2)(2+a)(2–a)
5.若将(2x)n–81分解成(4x2+9)(2x+3)(2x–3)，则n的值是_____________.
2(x+2)(x–2)
1．下列各多项式中，能用平方差公式分解因式的是( )A．－x2＋16　　 B．x2＋9C．－x2－4　　 D．x2－2y
2．(2019·无锡)分解因式4x2－y2的结果是( )A．(4x＋y)(4x－y)　　 B．4(x＋y)(x－y)C．(2x＋y)(2x－y)　　 D．2(x＋y)(x－y)3．已知x－y＝3，y－z＝2，x＋z＝4，则代数式x2－z2的值是( )A．9　　 B．18　　 C．20　　 D．24
4．因式分解：(1)9m2－4；解：原式＝(3m＋2)(3m－2).(2)－a3b＋ab；解：原式＝ab(1＋a)(1－a).
5．如图，一个圆环，外圆的半径为R，内圆的半径为r.(1)写出圆环面积的计算公式；(2)当R＝15.25 cm，r＝5.25 cm时，求圆环的面积(结果保留π).