数学24.1.2 垂直于弦的直径教学设计及反思

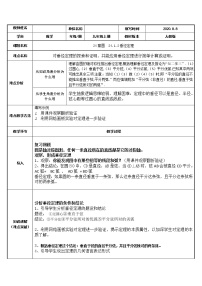
24.1.2　垂直于弦的直径

1．探索并了解圆的对称性和垂径定理．

2．能运用垂径定理解决几何证明、计算问题，并会解决一些实际问题．

▲重点

垂径定理、推论及其应用．

▲难点

发现并证明垂径定理．

◆问题导入

1．请同学们把手中的圆对折，你会发现圆是一个什么样的图形？

答：圆是轴对称图形，每一条直径所在的直线都是圆的对称轴．

2．请同学们再把手中的圆沿直径向上折，折痕是圆的一条什么呢？通过观察，你能发现直径与这条折痕的关系吗？

答：折痕是圆的一条弦，直径平分这条弦，并且平分弦所对的两条弧．

导入新课

通过折叠的方式可以找到圆形纸片的对称轴，在折的过程中你有何发现？

圆的对称性圆是轴对称图形，任意一条直径所在直线都是圆的对称轴.

探究新知

如何来证明圆是轴对称图形呢？

证明：连结OA、OB.

则OA＝OB．

又∵CD⊥AB，

∴直径CD所在的直线是AB的垂直平分线.

∴对于圆上任意一点，在圆上都有关于直线CD的对称点，即⊙O关于直线CD对称.

圆是轴对称图形，任何一条直径所在直线都是圆的对称轴.

此时，若将圆沿直径CD所在直线折叠，点A会与点B重合，你会发现有哪些重合的线段和劣弧呢？

垂径定理  垂直于弦的直径平分弦,并且平分弦所对的两条弧.

推导格式：

∵ CD是直径，CD⊥AB，

∴ AE=BE,

温馨提示：①过圆心 ；②垂直于弦； ③平分弦；

④平分弦所对的优弧 ； ⑤平分弦所对的劣弧.

巩固练习

1.如图，OE⊥AB于E，若⊙O的半径为10cm,

OE=6cm,则AB= （ ） cm.

2.如图， ⊙ O的弦AB＝8cm ，直径CE⊥AB于D，DC＝2cm，求半径OC的长.

四个变量

弦长a,半径r,

弦心距d（圆心到弦的距离），弓形高h。

两个关系

思想与方法：解决有关弦的问题，经常是过圆心作弦的弦心距（垂线段），或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件.

实践探究

把手中的圆对折，重复做几次，你发现了什么?

可以发现：圆是轴对称图形，

任何一条直径所在直线都是它的对称轴．　

利用手中的圆，动手折出与已知直径垂直的一条弦，并说明你折纸的理由。在折好的圆上标出如图所示的字母，讨论图中有哪些相等的量。

AE=BE，弧AD=弧BD，弧AC=弧BC

即直径CD平分弦AB，并且平分弧AB及弧ACB

由此，我们得到下面的定理：

垂直于弦的直径平分弦，并且平分弦所对的两条弧．

如图，在⊙O中，弦AB的长为8 cm，圆心O到弦AB的距离为3 cm，求⊙O的半径．

总结：常构造以弦、半径、弦心距为边的直角三角形，利用垂径定理和直角三角形的相关知识来解决问题。

已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C、D两点.

求证:AC=BD

变式：若隐去原图中的大圆，连接OA，OB，设OA=OB，

求证：AC＝BD。

课后练习

1．教材P83　练习第1，2题．

2．已知弓形的弦长为6cm，弓形的高为2cm，则这个弓形所在的圆的半径为____cm__．

3．如图，AB为⊙O的直径，E是的中点，OE交BC于点D，BD＝3，AB＝10，则AC＝__8__．

4．如图，⊙O中弦CD交半径OE于点A，交半径OF于点B，若OA＝OB，求证：AC＝BD.

证明：过点O作OG⊥CD于点G.

∵OG过圆心，∴CG＝DG.

∵OA＝OB.∴AG＝BG，∴CG－AG＝DG－BG，∴AC＝BD.

课堂小结

垂径定理及其推论，以及常用的辅助线(作垂径)和解题思路(构造由半径、半弦、弦心距组成的直角三角形)．

1．作业布置

(1)教材P90　习题24.1第8，11题；(2)对应课时练习．

2．教学反思