北京市第二中学2022-2023学年七年级上学期数学期中考试试卷(含答案)

这是一份北京市第二中学2022-2023学年七年级上学期数学期中考试试卷(含答案)，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
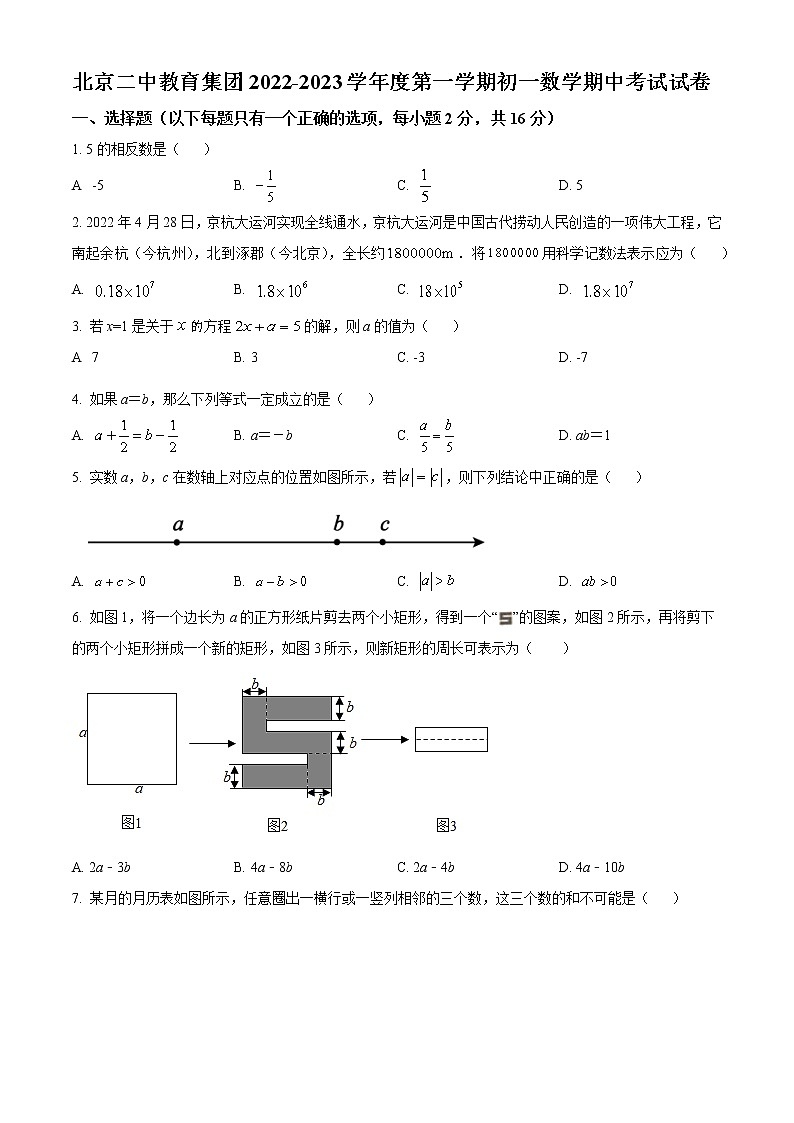
北京二中教育集团2022-2023学年度第一学期初一数学期中考试试卷一、选择题（以下每题只有一个正确的选项，每小题2分，共16分）1. 5的相反数是（    ）A -5 B.  C.  D. 52. 2022年4月28日，京杭大运河实现全线通水，京杭大运河是中国古代捞动人民创造的一项伟大工程，它南起余杭（今杭州），北到涿郡（今北京），全长约．将用科学记数法表示应为（    ）A.  B.  C.  D. 3. 若x=1是关于方程的解，则a的值为（    ）A 7 B. 3 C. -3 D. -74. 如果a＝b，那么下列等式一定成立的是（    ）A.  B. a＝－b C.  D. ab＝15. 实数a，b，c在数轴上对应点的位置如图所示，若，则下列结论中正确的是（    ）A.  B.  C.  D. 6. 如图1，将一个边长为a的正方形纸片剪去两个小矩形，得到一个“”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长可表示为（　　）A. 2a﹣3b B. 4a﹣8b C. 2a﹣4b D. 4a﹣10b7. 某月的月历表如图所示，任意圈出一横行或一竖列相邻的三个数，这三个数的和不可能是（    ）A. 24 B. 42 C. 50 D. 698. 在一次数学活动课上，某数学老师将1~10共十个整数依次写在十张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）．他先像洗扑克牌一样打乱这些卡片的顺序，然后把甲，乙，丙，丁，戊五位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上，写出的结果依次是：甲：11；乙：4；丙：15；丁：8；戊：17，则甲同学手里拿的卡片的数字是（    ）A. 2和9 B. 3和8 C. 4和7 D. 5和6二、填空题（共16分，每小题2分）9. 请写出一个比大的负有理数：_____．（写出一个即可）10. 月球表面的白天平均温度为零上126℃，夜间平均温度为零下150℃．如果零上126℃记作＋126℃，那么零下150℃应该记作______℃．11. 已知，则______．12. 如果数轴上的点A对应的数为﹣1，那么与A点相距3个单位长度的点所对应的有理数为_____．13. 如果与是同类项，那么的值是______．14. 下列各数：，0，，，，，其中正整数有_______个．15. 若与互为相反数，则的值为______．16. 对于两个不相等的有理数a，b，我们规定符号表示a，b两数中较大的数，例如．按照这个规定，方程的解为_______．三、解答题（共68分，第17-20题，每题5分，第21题6分，第22-23题，每题5分，第24-26题，每题6分，第27-28题，每题7分）17. 计算：．18. 计算：．19. 计算：．20. 计算：．21. 先化简，再求值：，其中，．22. 解方程：．23. 解方程：．24. 关于的一元一次方程，其中是正整数．（1）当时，求方程的解；（2）若方程有正整数解，求的值．25. 某同学模仿二维码的方式为学校设计了一个身份识别图案系统：在的正方形网格中，黑色正方形表示数字1，白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下：把第i行，第j列表示的数字记为（其中i，j=1，2，3，4），如图1中第2行第1列的数字=0；对第i行使用公式进行计算，所得结果表示所在年级，表示所在班级，表示学号的十位数字，表示学号的个位数字.如图1中，第二行，说明这个学生在5班.（1）图1代表的学生所在年级是______年级，他的学号是_________；（2）请仿照图1，在图2中画出八年级4班学号是36的同学的身份识别图案26. 为响应国家节能减排政策，某班开展了节电竞赛活动．通过随手关灯、提高夏季空调温度、及时关闭电源等行为，小明和小玲两位同学半年共节电55度．据统计，节约1度电相当于节约0.4千克“标准煤”，在节电55度产生的节煤量中，小明“节煤量”的2倍比小玲多8千克．设小明半年节电x度．请回答下面的问题：（1）用含x的代数式表示小玲半年节电量为_______度，用含x的代数式表示这半年小明节电产生的“节煤量”为_______千克，用含x的代数式表示这半年小玲节电产生的“节煤量”为_______千克；（不需要化简）（2）请列方程求出小明半年节电的度数．27. 己知a，b在数轴上的位置如图所示：（1）用“>”、“<”或“=”填空：，，；（2）化简：；（3）若，x为数轴上任意一点所对应数，则代数式的最小值是______；此时x的取值范围是______．28. 我们规定：对于数轴上不同的三个点M，N，P，当点M在点N左侧时，若点P到点M的距离恰好为点P到点N的距离的k倍，且k为正整数，（即），则称点P是“整k关联点”如图，已知在数轴上，原点为O，点A，点B表示的数分别为．（1）原点O________（填“是”或“不是”）“整k关联点”；（2）若点C是“整2关联点”，则点C所表示的数_______；（3）若点A沿数轴向左运动，每秒运动2个单位长度，同时点B沿数轴向右运动，每秒运动1个单位长度，则运动时间为________秒时，原点O恰好是“整k关联点”，此时k值为_______．（4）点Q在A，B之间运动，且不与A，B两点重合，作“整2关联点”，记为，作“整3关联点”，记为，且满足，分别在线段AQ和BQ上．当点Q运动时，若存在整数m，n，使得式子为定值，求出m，n满足的数量关系．
北京二中教育集团2022-2023学年度第一学期初一数学期中考试试卷一、选择题（以下每题只有一个正确的选项，每小题2分，共16分）【1题答案】【答案】A【2题答案】【答案】B【3题答案】【答案】B【4题答案】【答案】C【5题答案】【答案】C【6题答案】【答案】B【7题答案】【答案】C【8题答案】【答案】C二、填空题（共16分，每小题2分）【9题答案】【答案】（答案不唯一）．【10题答案】【答案】-150【11题答案】【答案】【12题答案】【答案】﹣4或2【13题答案】【答案】【14题答案】【答案】1【15题答案】【答案】【16题答案】【答案】三、解答题（共68分，第17-20题，每题5分，第21题6分，第22-23题，每题5分，第24-26题，每题6分，第27-28题，每题7分）【17题答案】【答案】【18题答案】【答案】【19题答案】【答案】-8【20题答案】【答案】1【21题答案】【答案】，【22题答案】【答案】【23题答案】【答案】【24题答案】【答案】（1）；（2）1或4
 【25题答案】【答案】（1）七；28；（2）见解析【26题答案】【答案】（1），，    （2）【27题答案】【答案】（1）    （2）    （3）3，【28题答案】【答案】（1）不是    （2）2或    （3）2，1    （4）