北京市第四中学2022--2023学年八年级上学期期中数学试卷(含答案)

这是一份北京市第四中学2022--2023学年八年级上学期期中数学试卷(含答案)，共11页。
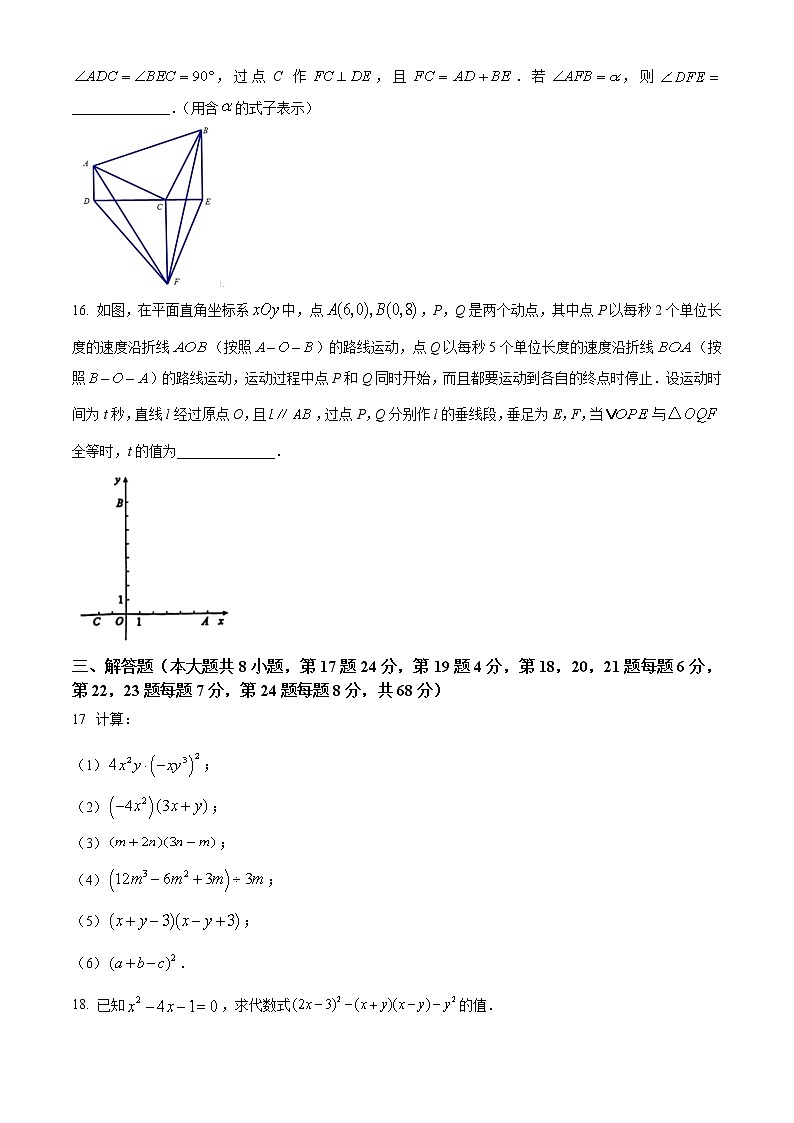
数学试卷班级_______     姓名_______     学号_______     成绩_______考生须知：1．本试卷共8页，第一部分共24道小题，第二部分共2道小题，满分110分；考试时间100分钟2．在试卷和答题卡上准确填写班级、姓名和学号3．答案一律填写在答题卡上，在试卷上作答无效4．在答题卡上，选择题用2B铅笔作答，其他试题用黑色字迹签字笔作答第一部分一、选择题（本大题共8小题，每小题2分，共16分）1. 下列各式计算正确的是（ ）.A.  B. C  D. 2. 下列各组线段能组成三角形的是（    ）A.  B.  C.  D. 3. 如图，在中，是的边上的中线，那么可以证明，这里证明全等所使用的判定方法是（    ）A.  B.  C.  D. 4. 如图所示，，，，，，则（    ）A.  B.  C.  D. 无法计算5. 如图，在由线段组成的平面图形中，，则的度数为（    ）．A  B.  C.  D. 6. 若，则值为（    ）A. 27 B. 23 C. 24 D. 37. 在中，，延长至D，使，连接，则的长度的取值范围是（    ）．A.  B.  C.  D. 8. 如图，在中，，则的度数是（    ）A  B.  C.  D. 二、填空题（本大题共8小题，每小题2分，共16分）9. 在中，，，则______________．10. 一个多边形的内角和是，这个多边形的边数是______．11. 已知等腰三角形的周长为20，其中一边的长为6，则底边的长为______________．12. 已知锐角的一个内角是，，那么的外角是______________．13. 若是一个完全平方式，则k的值是________．14. 若与的乘积中不含x的二次项，则实数m的值为______________．15. 如图，在中，，D、C、E三点在一条直线上，且，过点C作，且．若，则______________．（用含的式子表示） 16. 如图，在平面直角坐标系中，点，P，Q是两个动点，其中点P以每秒2个单位长度的速度沿折线（按照）的路线运动，点Q以每秒5个单位长度的速度沿折线（按照）的路线运动，运动过程中点P和Q同时开始，而且都要运动到各自的终点时停止．设运动时间为t秒，直线l经过原点O，且，过点P，Q分别作l的垂线段，垂足为E，F，当与全等时，t的值为______________．三、解答题（本大题共8小题，第17题24分，第19题4分，第18，20，21题每题6分，第22，23题每题7分，第24题每题8分，共68分）17 计算：（1）；（2）；（3）；（4）；（5）；（6）．18. 已知，求代数式的值．19. 要求：铅笔作图（可以借助带刻度的直尺、三角板和量角器）：已知（如图），求作：（1）的中线；（2）的角平分线；（3）的高线；（4）若（其中C表示周长），且，则______________．20. 如图，点B，F，C，E在一条直线上BF＝CE，AC＝DF．（1）在下列条件①∠B＝∠E；②∠ACB＝∠DFE；③AB＝DE；④AC∥DF中，只添加一个条件就可以证得△ABC≌△DEF，则所有正确条件的序号是　　．（2）根据已知及（1）中添加的一个条件证明∠A＝∠D．21. 如图，在中，，于点H，点D为上的一点，且，连接并延长交于点E．（1）请补全图形；（2）写出与的数量关系和位置关系并证明．22. 在乘法公式的学习中，我们采用了构造几何图形的方法研究问题，借助直观、形象的几何模型，加深对乘法公式的认识和理解，从中感悟数形结合的思想方法，感悟几何与代数内在的统一性，根据课堂学习的经验，解决下列问题：图1                    图2 （1）如图1，将一张长方形纸板按图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小长方形，且，观察图形，用不同的方法表示这块长方形纸板的面积，可得等式为____________________________；（2）将图2中边长为a和b的正方形拼在一起，B，C，G三点在同一条直线上，连接和，若这两个正方形的边长满足，，请求出阴影部分的面积．（3）若图1中每块小长方形的面积为6，四个正方形的面积之和为48，请直接写出图中所有裁剪线（虚线部分）的长度之和．23. 如图，在中，，D为边上一点，平分，且，若，，求的长．24. 喜欢动手的小马同学收集了很多套三角板，以下是他利用三角板进行的数学探究：（1）小马同学将两个大小相同的含有，的三角板如图1所示放置，即，连接、交于点F，小马同学发现，请给出证明：（2）小马同学将两个大小不同的等腰直角三角板如图2所示放置，即，连接交于点F．当时，请写出与之间的数量关系，并证明．第二部分  附加题（共10分）25. 阅读材料：我们已经学习过完全平方公式．对于多项式，虽然不能写成某个代数式的平方形式，但是可以写成，即一个含x的代数式的平方与另一个数的和的形式．更一般的，对于二次项系数不为1的二次三项式，它总是可以化为的形式，我们把这种代数式的恒等变形叫做配方．例如：，这就是一个配方的过程．根据以上内容回答下列问题：（1）代数式经配方可化为______________．（2）已知，那么的值为______________．（3）已知x、y为实数，求代数式的最小值及取到最小值时x、y的值．26. 小聪和小明两位同学在学习全等三角形时积极思考，提出了以下两个问题：问题1：如图1，中，，，是的角平分线，求的值．小聪同学经过思考，发现可以过D作于M，于N，利用与的面积比来解决这个问题．问题2：如图2，为等边三角形，点D为外一点，，连接，探究三者之间的的数量关系．小明同学经过思考，发现可以在上截取，构造等边三角形，从而解决这个问题．（1）根据两位同学的思考，完成问题1、2的解答（直接写出结果）．（2）根据问题1、2的结论，解决下面问题：如图3，和都是等边三角形，且B，C，E三点共线，连接交于点F，连接，设，，，若，直接写出的值．
数学试卷班级_______     姓名_______     学号_______     成绩_______考生须知：1．本试卷共8页，第一部分共24道小题，第二部分共2道小题，满分110分；考试时间100分钟2．在试卷和答题卡上准确填写班级、姓名和学号3．答案一律填写在答题卡上，在试卷上作答无效4．在答题卡上，选择题用2B铅笔作答，其他试题用黑色字迹签字笔作答第一部分一、选择题（本大题共8小题，每小题2分，共16分）【1题答案】【答案】A【2题答案】【答案】A【3题答案】【答案】D【4题答案】【答案】B【5题答案】【答案】C【6题答案】【答案】B【7题答案】【答案】A【8题答案】【答案】D二、填空题（本大题共8小题，每小题2分，共16分）【9题答案】【答案】【10题答案】【答案】6##六【11题答案】【答案】6或8##8或6【12题答案】【答案】80或140##140或80【13题答案】【答案】
 【14题答案】【答案】1【15题答案】【答案】##【16题答案】【答案】或或三、解答题（本大题共8小题，第17题24分，第19题4分，第18，20，21题每题6分，第22，23题每题7分，第24题每题8分，共68分）【17题答案】【答案】（1）    （2）    （3）    （4）    （5）    （6）【18题答案】【答案】12【19题答案】【答案】（1）答案见详解；    （2）答案见详解；    （3）答案见详解；    （4）8．【20题答案】【答案】（1）②③④；（2）添加条件∠ACB＝∠DFE，理由详见解析．【21题答案】【答案】（1）图见解析    （2），，理由见解析【22题答案】【答案】（1）    （2）8    （3）36【23题答案】【答案】7【24题答案】【答案】（1）见解析    （2），证明见解析第二部分  附加题（共10分）【25题答案】【答案】（1）    （2）    （3）代数式的最小值为，此时，【26题答案】【答案】（1）；；    （2）．