2022-2023学年天津市第一中学高一上学期期中数学试题

这是一份2022-2023学年天津市第一中学高一上学期期中数学试题，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
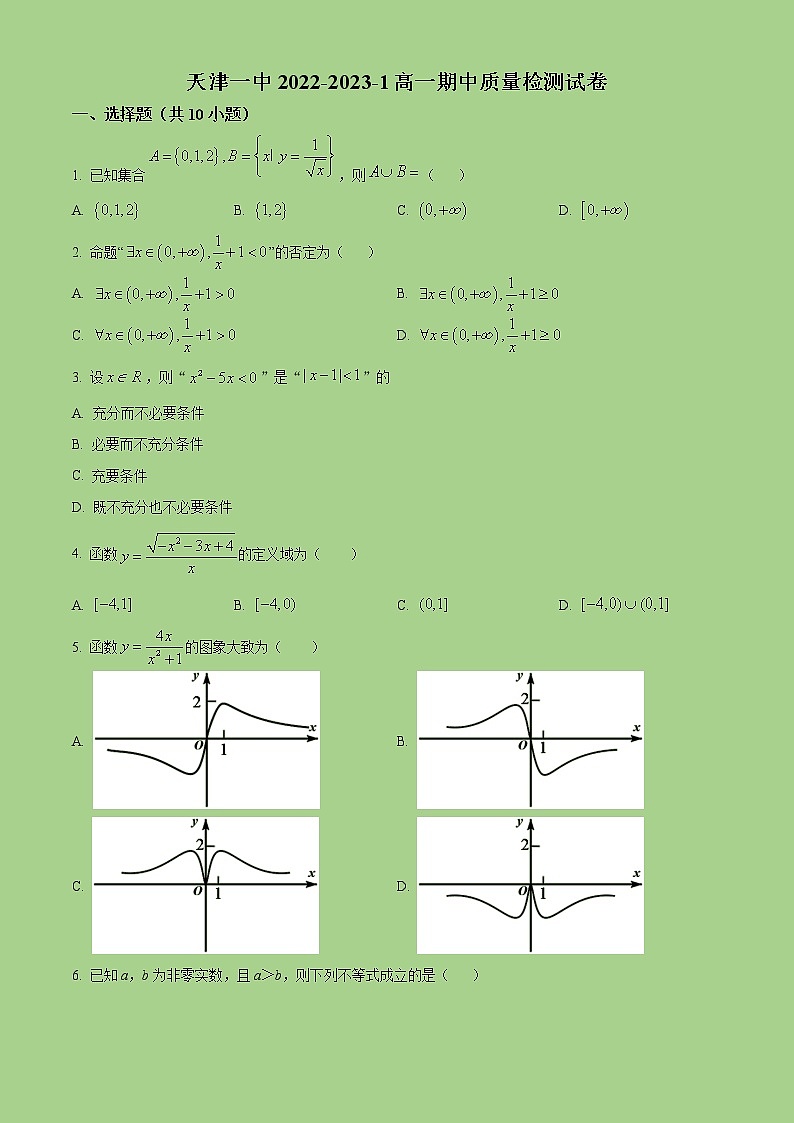
天津一中2022-2023-1高一期中质量检测试卷一、选择题（共10小题）1. 已知集合，则（    ）A.  B.  C.  D. 2. 命题“”的否定为（    ）A.  B. C.  D. 3. 设，则“”是“”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件4. 函数的定义域为（    ）A.  B.  C.  D. 5. 函数的图象大致为（    ）A.  B. C.  D. 6. 已知a，b为非零实数，且a＞b，则下列不等式成立的是（    ）A  B.  C.  D. 7. 若函数，则（    ）A. -2 B. 2 C. -4 D. 48. 若函数y=f（x)是奇函数，且函数F(x)=af(x)+bx+2在（0，+∞，)上有最大值8，则函数y=F(x)在(－∞，，0)上有 A. 最小值－8 B. 最大值－8C. 最小值－6 D. 最小值－49. 已知函数定义域为R，是偶函数，，在上单调递增，则不等式的解集为（    ）A  B. C.  D. 10. 已知定义在上的奇函数，当时，若对于任意的实数有成立，则正数的取值范围是（    ）A.  B.  C.  D. 二、填空题（共6小题）11. 已知幂函数在为增函数，则实数的值为___________.12. 若命题“使”是假命题，则实数的取值范围为_____，13. 已知函数的，则其值域为_____________.14. 函数的单调递增区间是_____．15. 已知，且，则的最小值为_________．16. 已知函数，①若对任意，且都有，则实数的取值范围为___________；②若在上的值域为，则实数的取值范围为___________.三、解答题（共4小题）17. 已知集合，集合，（1）若，求和；（2）若，求实数的取值范围.18. 函数是定义在实数集上的奇函数，当时，.（1）判断函数在的单调性，并给出证明；（2）求函数解析式；（3）若对任意的，不等式恒成立，求实数的取值范围.19 设函数（1）若，且，求的最小值；（2）若，且在上恒成立，求实数的取值范围.20. 已知函数是定义域上的奇函数，且．（1）求函数的解析式，判断函数在上的单调性并证明；（2）令，若函数在上有两个零点，求实数的取值范围；（3）令，若对，都有，求实数的取值范围．
 
天津一中2022-2023-1高一期中质量检测试卷一、选择题（共10小题）【1题答案】【答案】D【2题答案】【答案】D【3题答案】【答案】B【4题答案】【答案】D【5题答案】【答案】A【6题答案】【答案】A【7题答案】【答案】C【8题答案】【答案】D【9题答案】【答案】A【10题答案】【答案】D二、填空题（共6小题）【11题答案】【答案】4【12题答案】【答案】【13题答案】【答案】【14题答案】【答案】【15题答案】【答案】4【16题答案】【答案】    ①.     ②. 三、解答题（共4小题）【17题答案】【答案】（1），    （2）【18题答案】【答案】（1）函数在上单调递减，证明见解析    （2）    （3）【19题答案】【答案】（1）；（2）.【20题答案】【答案】（1）；函数在上单调递减，在上单调递增，证明见解析；（2）；（3）