2022-2023八上期中 海淀区第五十七中学数学试卷

这是一份2022-2023八上期中 海淀区第五十七中学数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
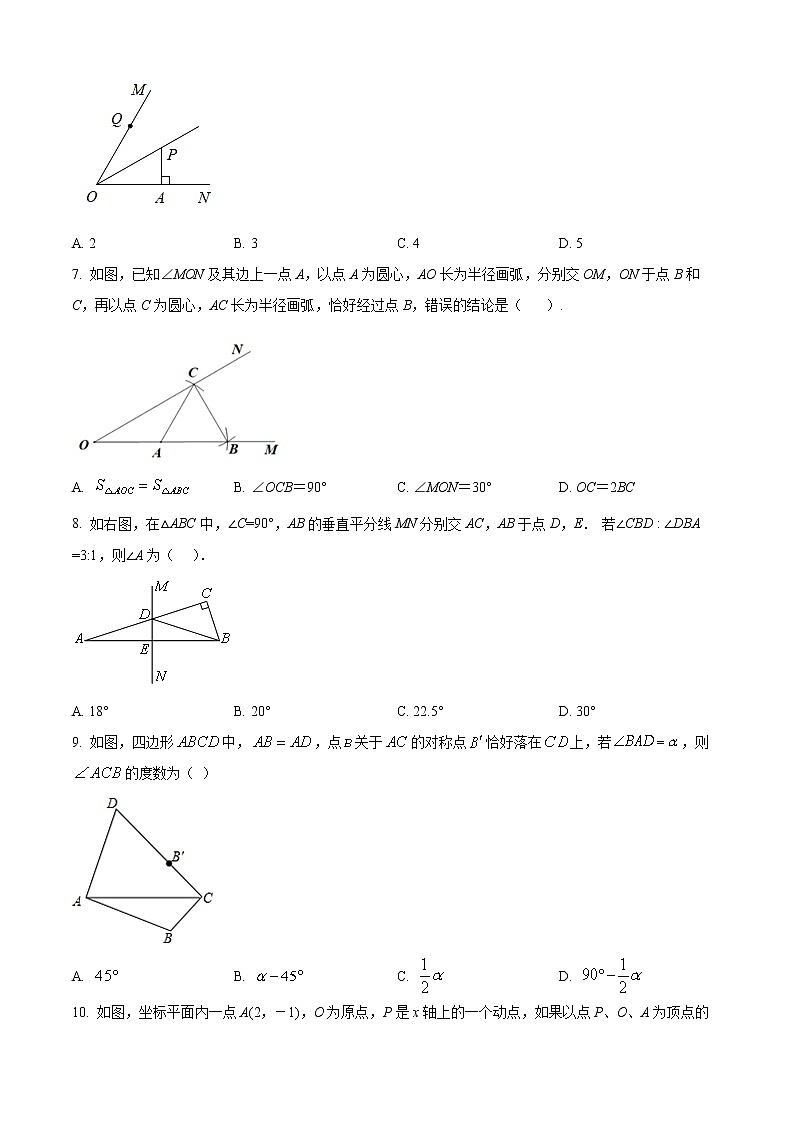
2022-2023学年度初二年级第一学期数学期中练习一、选择题1. 下列平面图形中，不是轴对称图形是（ ）A.  B.  C.  D. 2. 正六边形的内角和为（    ）A. 180° B. 360° C. 720° D. 1440°3. 如图，在平面直角坐标系xOy中，点P(，5)关于y轴的对称点的坐标为（ ）A. ( ，) B. (3，5) C. (3．) D. (5，)4. 如图，左边为参加2019年国庆70周年阅兵的武警摩托车礼宾护卫队，如果将每位队员看成一个点，队形可近似看成由右边所示的若干个正方形拼成的图形，其中与△ABC全等的三角形是（  ）                     A. △AEG B. △ADF C. △DFG D. △CEG5. 已知一个等腰三角形一内角的度数为80°，则这个等腰三角形底角的度数为（    ）A. 100° B. 80° C. 20°或80° D. 50°或80°6. 如图，OP平分，于点A，点Q是射线OM上的一个动点．若，则PQ的最小值为（    ）A. 2 B. 3 C. 4 D. 57. 如图，已知∠MON及其边上一点A，以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C，再以点C为圆心，AC长为半径画弧，恰好经过点B，错误的结论是（    ）.A.  B. ∠OCB＝90° C. ∠MON＝30° D. OC＝2BC8. 如右图，在△ABC中，∠C=90°，AB的垂直平分线MN分别交AC，AB于点D，E． 若∠CBD : ∠DBA =3:1，则∠A为（   ）． A. 18° B. 20° C. 22.5° D. 30°9. 如图，四边形中，，点关于的对称点恰好落在上，若，则的度数为（ ）A.  B.  C.  D. 10. 如图，坐标平面内一点A(2，－1)，O为原点，P是x轴上的一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为( )A. 2 B. 3 C. 4 D. 5二、填空题11. 如果等腰三角形的两条边长分别为23cm和10cm，那么第三边的长为_________cm．12. 已知一个正多边形的内角和为1440°，则它的一个外角的度数为_____度．13. 如图，在△ABC中，AB=AC，D为BC上一点，且CD=AD ，AB=BD，则∠B的度数为__________．14. 如图1，三角形纸片ABC，，将其折叠，如图2，使点A与点B又重合，折痕为ED，点E、D分别在AB，AC上，如果，那么的度数为__________．15. 在△ABC中，AB＝10，AC＝6，AD是BC边上的中线，则AD的取值范围是___________．16. 如图，AB＝AC，BD⊥AC，∠CBD＝α，则∠A＝_____（用含α的式子表示）．17. 如图，在中，边的垂直平分线分别交于于点，交于点，若的周长为8，AE=3，则的周长为___________.18. 如图，已知点O是△ABC内一点，且点O到三边距离相等，∠A=40°，则∠BOC=_____．19. 已知：如图，在等边和等边中，点A在DE的延长线上，如果，那么__________度．20. 下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程．已知：线段a求作：等腰△ABC，使AB=AC，BC=a，BC边上的高为2a，作法：如图，(1)作线段BC=a；(2)作线段BC的垂直平分线DE交BC于点F；(3)在射线FD上顺次截取线段FG=GA=a，连接AB，AC，所以△ABC即为所求作的等腰三角形．请回答：得到△ABC是等腰三角形的依据是：___________________．三、解答题21. 作图题：（1）作出与关于y轴对称的图形；（2）若图中一个小正方形边长为一个单位长度，请写出各点的坐标：__________；__________；__________；（3）求的面积．（4）若点P为y轴上一点，使点P到A、B的距离和最小，标出点P．22. 如图，已知点M、N和∠AOB ，用尺规作图作一点P，使P到点M、N的距离相等，且到∠AOB两边的距离相等．（保留作图痕迹，不写作法） 23. 如图，点B、F、C、E在一条直线上，BF＝EC，AC＝DF，AC∥DF．求证：∠A＝∠D．24.  如图，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．（1）求证：AE＝CD；（2）若AC＝12cm，求BD的长25. 在△ABC中，AB=AC，点D是直线BC上一点（点D不与点B，C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．（1）求证：△ABD≌△ACE；（2）∠BCE和∠BAC之间有怎样的数量关系？说明理由．26. 在中，为锐角，，AD平分交BC于点D，BC的垂直平分线交AD延长线于点E，交BC于点F，如图，若，判断AC、CE和AB之间有怎样的数量关系并加以证明．27. 如图，CN是等边△ABC的外角∠ACM内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P．（1）依题意补全图形；（2）若∠ACN＝α，求∠BDC大小（用含α的式子表示）；（3）用等式表示线段PB，PC与PE之间的数量关系，并证明．28. 在平面直角坐标中，直线l为二、四象限角平分绒，图形T关于x轴的对称图形称为图形T的一次反射图形，记作图形；图形关于直线l的对称图形称为图形T的二次反射图形，记作图形．例如，点一次反射点为，二次反射点为．根据定义，回答下列问题：（1）①点的一次反射点为______，二次反射点为______；②当点A在第二象限时，点、，中可以是点A的二次反射点的是______；（2）若点A在第一象限，点、分别是点A的一次、二次反射点，为等边三角形，求射线与y轴所夹锐角的度数；（3）已知点，．若以为边正方形的二次反射图形与直线有公共点，则n的取值范围为______．