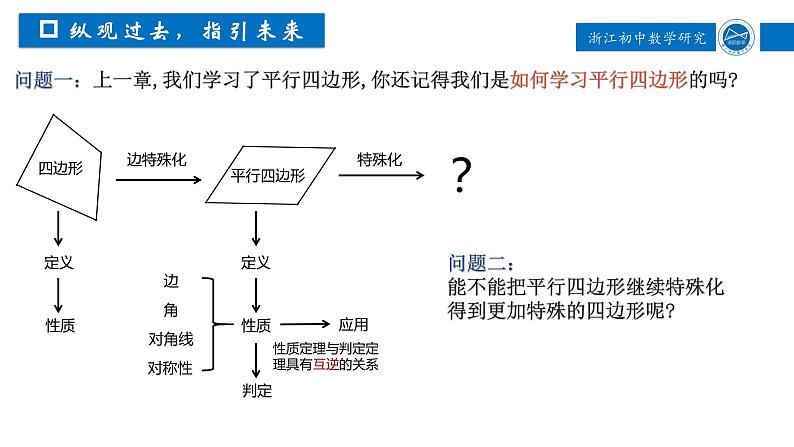



浙教版八年级下册5.1 矩形评课ppt课件
展开问题三: 一位师傅现有两条长度为3分米和两条长度为6分米的铝合金材料, 请问这位师傅可以做出多少种不同的平行四边形框架?
问题四: 主人想把它做成面积最大的平行四边形,你能帮助这位师傅完成任务吗?
无数种,因为平行四边形具有不稳定性.
5.1.1矩形
浙教版数学八年级下册第五单元第一节第一课时
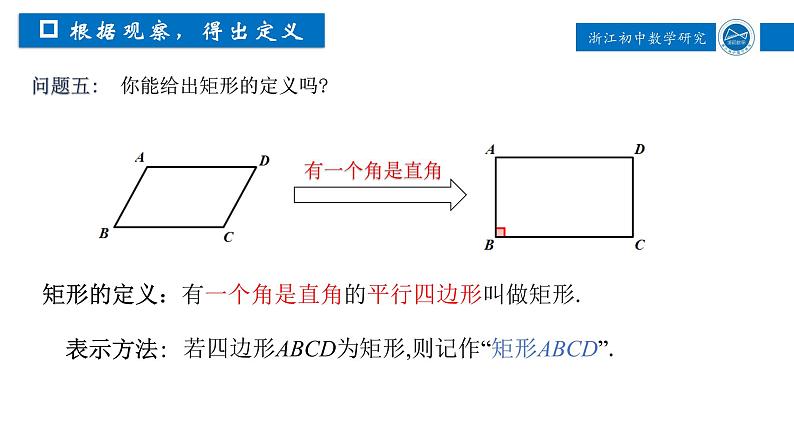
矩形的定义:有一个角是直角的平行四边形叫做矩形.
问题五: 你能给出矩形的定义吗?
若四边形ABCD为矩形,则记作“矩形ABCD”.
生活中哪些物体能抽象出矩形?你能举几个例子吗?
小学里学过的长方形,正方形都是矩形.
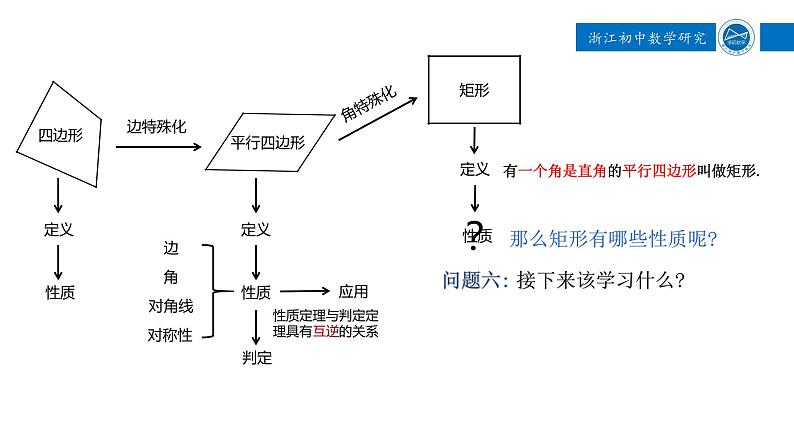
问题六: 接下来该学习什么?
有一个角是直角的平行四边形叫做矩形.
那么矩形有哪些性质呢?
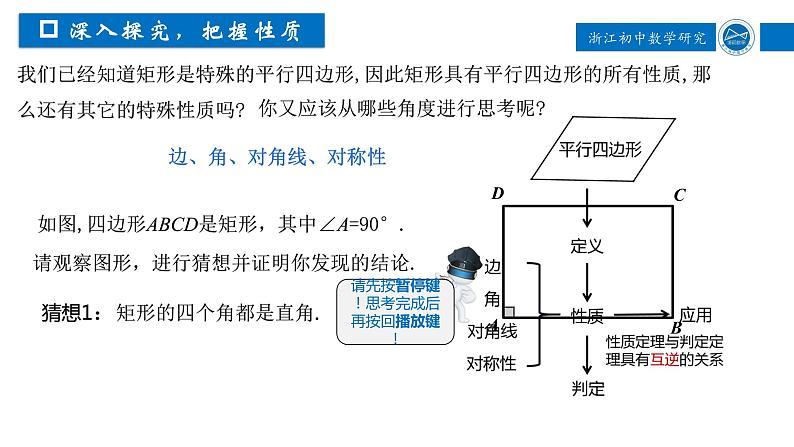
我们已经知道矩形是特殊的平行四边形,因此矩形具有平行四边形的所有性质,那么还有其它的特殊性质吗?
请观察图形,进行猜想并证明你发现的结论.
如图,四边形ABCD是矩形,其中∠A=90°.
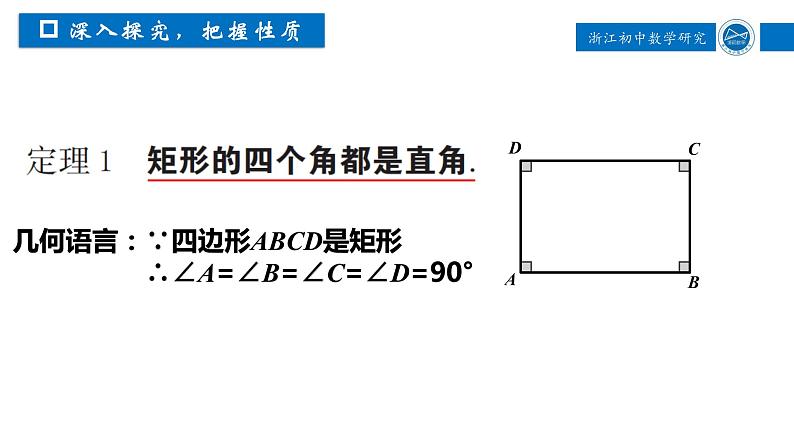
猜想1:矩形的四个角都是直角.
你又应该从哪些角度进行思考呢?
边、角、对角线、对称性
几何语言:∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=90°
若将矩形ABCD的对角线连结,你还发现了什么?
猜想2:矩形的对角线相等.
已知:如图,AC,BD 是矩形ABCD的对角线求证:BD=AC
∵四边形ABCD是矩形
∴∠DAB=∠CBA=90°
∴△DAB≌△CBA(SAS)
(平行四边形的对边相等)
(矩形的四个角都是直角)
几何语言:∵四边形ABCD是矩形 ∴AC=BD
思考:图中是否有全等三角形和等腰三角形?
全等三角形:△ABD≌△BAC≌△CDB≌△DCA,△AOD≌△COB, △COD≌△AOB.
等腰三角形: △AOD,△COB,△COD,△AOB.
我们知道平行四边形是中心对称图形,所以矩形也是中心对称图形,那么它在对称性上是否还有特殊性呢?请拿出一张矩形纸片,折一折.
矩形的对称性:矩形既是中心对称图形, 又是轴对称图形. 它有至少2条对称轴.
如图,矩形ABCD的对角线AC,BD相交于点O, ∠BOC=50°,求∠DBA的度数.
解:∵四边形ABCD是矩形
∴OC=OB(平行四边形的对角线互相平分)
∴∠DBA= 90°-∠CBO=25°
又∵∠CBA=90°(矩形四个角都是直角)
∴AC=BD (矩形的对角线相等)
(1)请判断△AOD的形状;(2)求矩形对角线的长.
例1 已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠COD=120°,AD=4cm.
解:(1)△AOD是等边三角形,理由如下:
又∵∠AOD=180°-∠COD=180°-120°=60°
∴△AOD是等边三角形(有一个角是60°的等腰三角形是等边三角形)
(平行四边形的对角线互相平分)
(2)∵△AOD是等边三角形
∴AC=BD=2AO=8cm
(1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由;
(2)以DE为一边作一个矩形,要求另外两个顶点也在方格顶点上.
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
∴DC2+BC2=BD2
∴四边形ABCD是矩形
解:(1)四边形ABCD是矩形,理由如下:
(2)如图,四边形DEHG,四边形DEAF即为所求.
已知:如图,矩形ABCD中,E是BC上一点,且AE=AD,DF⊥AE于点F. 求证:CE=FE.
∴∠B=90°,AD//BC,AD=BC
在△ADF 和△EAB中
∴BC-BE=AD-BE=AE-AF
有一个角是直角的平行四边形是矩形.
矩形的四个角都是直角.
矩形既是中心对称图形, 又是轴对称图形.
浙教版八年级下册5.1 矩形教学演示ppt课件: 这是一份浙教版八年级下册5.1 矩形教学演示ppt课件,共12页。PPT课件主要包含了回顾旧知引入新知,特殊化,创设情境探究新知,创设情境形成概念,四边形,平行四边形,联系生活欣赏图片,电脑显示器,类比研究探究性质,对边平行且相等等内容,欢迎下载使用。
初中数学浙教版八年级下册5.1 矩形备课课件ppt: 这是一份初中数学浙教版八年级下册5.1 矩形备课课件ppt,共17页。PPT课件主要包含了学习目标,对边平行且相等,复习导入,平行四边形,ABCD,∴ACBD,又BCCB,例题讲解,随堂练习,∵∠ABC90°等内容,欢迎下载使用。
初中数学浙教版八年级下册5.1 矩形图文课件ppt: 这是一份初中数学浙教版八年级下册5.1 矩形图文课件ppt,共16页。PPT课件主要包含了定义法,定理2等内容,欢迎下载使用。













