2020-2021学年第五章 特殊平行四边形5.3 正方形评课ppt课件

这是一份2020-2021学年第五章 特殊平行四边形5.3 正方形评课ppt课件，共18页。PPT课件主要包含了创设问题引入新课，自主探究形成概念，深入探究归纳小结，一个角是直角，一组邻边相等，定义法，矩形法，菱形法，练习巩固掌握新知，深入探究构建新知等内容，欢迎下载使用。
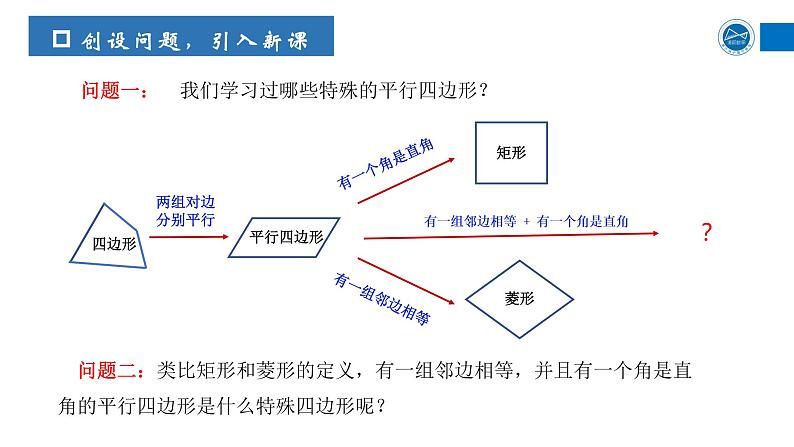
问题一： 我们学习过哪些特殊的平行四边形？
有一组邻边相等 + 有一个角是直角
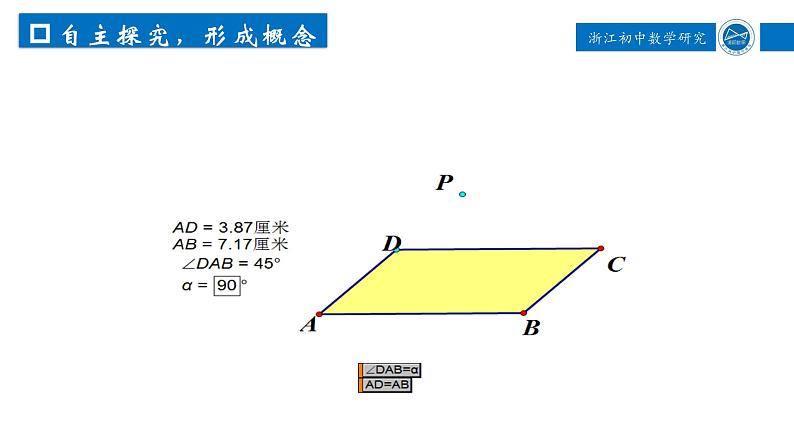
问题二：类比矩形和菱形的定义，有一组邻边相等，并且有一个角是直角的平行四边形是什么特殊四边形呢？
定义：有一组邻边相等，并且有一个角是直角的平行四边形 叫做正方形（square）.
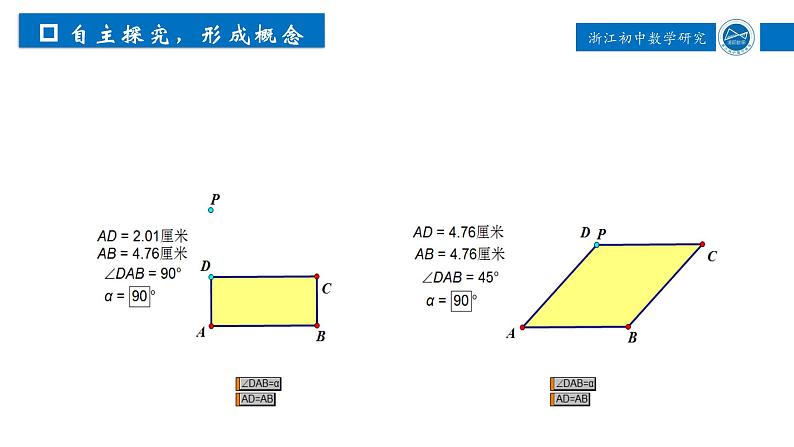
定义是判定正方形一种方法.从矩形的边去考虑可以得出有一组邻边相等的矩形是正方形.从菱形的角去考虑可以得出有一个角是直角的菱形是正方形.
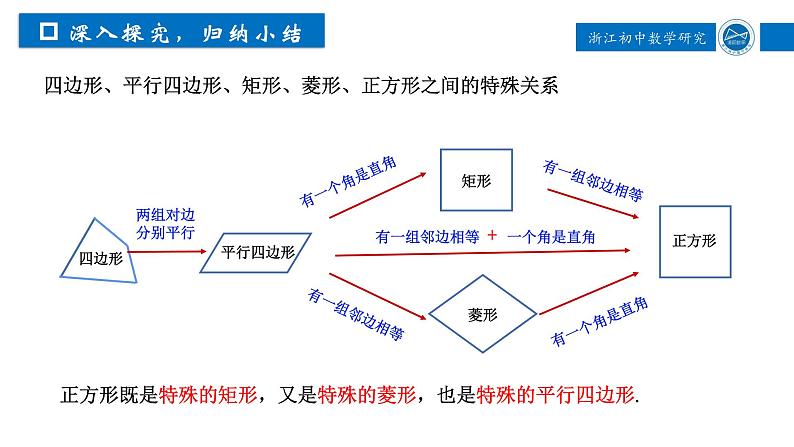
四边形、平行四边形、矩形、菱形、正方形之间的特殊关系
正方形既是特殊的矩形，又是特殊的菱形，也是特殊的平行四边形.
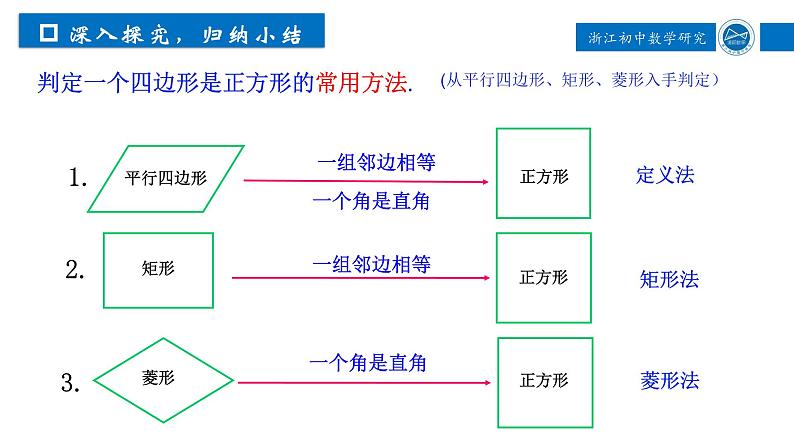
判定一个四边形是正方形的常用方法.
(从平行四边形、矩形、菱形入手判定）
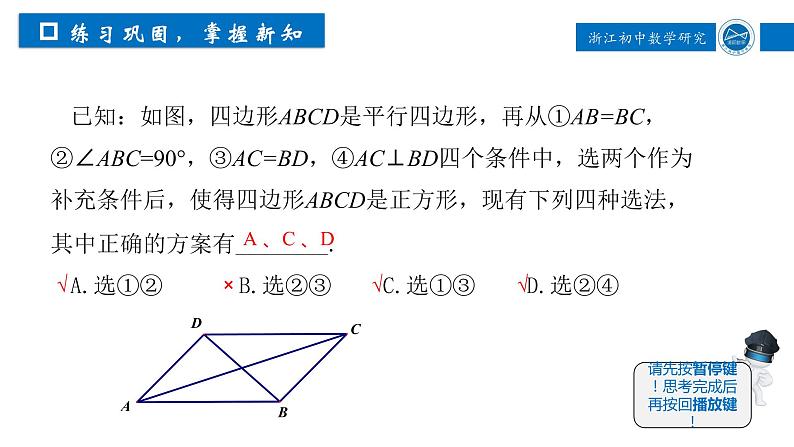
已知：如图，四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中正确的方案有________.A.选①② B.选②③ C.选①③ D.选②④
问题三：还有没有其他方法可以判定四边形是正方形？
1.有一个角为直角的平行四边形.
3.对角线相等的平行四边形.
2.有三个角为直角的四边形.
1.有一组邻边相等的平行四边形.
3.对角线互相垂直的平行四边形.
2.四条边相等的四边形.
对角线互相垂直平分且相等的四边形是正方形.
(1) 对角线互相垂直，一个角是直角的四边形是正方形. （ ）(2) 如果一个菱形的对角线相等，那么它一定是正方形. （ ）(3) 如果一个矩形的对角线互相垂直，那么它一定是正方形.（ ）(4) 四条边相等，且有一个角是直角的四边形是正方形. （ ）(5) 对角线互相垂直且相等的四边形是正方形. （ ）
例1 已知：如图，在Rt△ABC 中，∠ACB =90°，CD 是∠ACB 的平分线，DE⊥BC，DF⊥AC，垂足分别为E，F. 求证：四边形CFDE是正方形.
1.要证明四边形CFDE是正方形，从已知条件看，你准备先证明它是矩形还是菱形？为什么？
2.根据“有一组邻边相等的矩形是正方形”，你准备选择哪一组邻边相等？
3.根据哪个性质能说明DE=DF ?
证明：∵ DE⊥BC，DF⊥AC，∴ ∠DEC=∠DFC=90°.而∠ACB=90°，∴ 四边形CFDE为矩形（有三个角是直角的四边形是矩形）.又∵ CD是∠ACB的平分线，∴ ∠1=∠2，∴ DE=DF（角平分线的性质定理）.∴ 四边形CFDE是正方形（有一组邻边相等的矩形是正方形）.
已知：如图，在Rt△ABC中，∠C＝90°，∠BAC，∠ABC 的 平分线相交于点D，DE⊥BC，DF⊥AC，垂足分别为E，F．求证：四边形CEDF是正方形．
1.根据有三个角是直角的四边形是矩形可证明四边形CEDF是矩形.
2.只要证得一组邻边相等即可.
3.根据有一组邻边相等的矩形是正方形可得结论．
AD平分∠BAC，DF⊥AC，DG⊥AB
BD平分∠ABC，DE⊥BC,DG⊥AB
已知：如图，在Rt△ABC中，∠C＝90°，∠BAC，∠ABC的 平分线相交于点D，DE⊥BC，DF⊥AC，垂足分别为E，F．求证：四边形CEDF是正方形．
证明：过点D 作DG⊥AB，垂足为点．∵∠C＝90°，DE⊥BC，DF⊥AC，∴∠DEC=∠DFC=∠C=90°，∴四边形CEDF是矩形.
∵∠BAC，∠ABC的平分线相交于点D， DE⊥BC，DF⊥AC，DG⊥AB，∴DF＝DG，DE＝DG，∴DE＝DF．
∴四边形CEDF是正方形．
有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形.