

初中数学北师大版八年级上册1 函数同步训练题
展开4.1函数
一、单选题
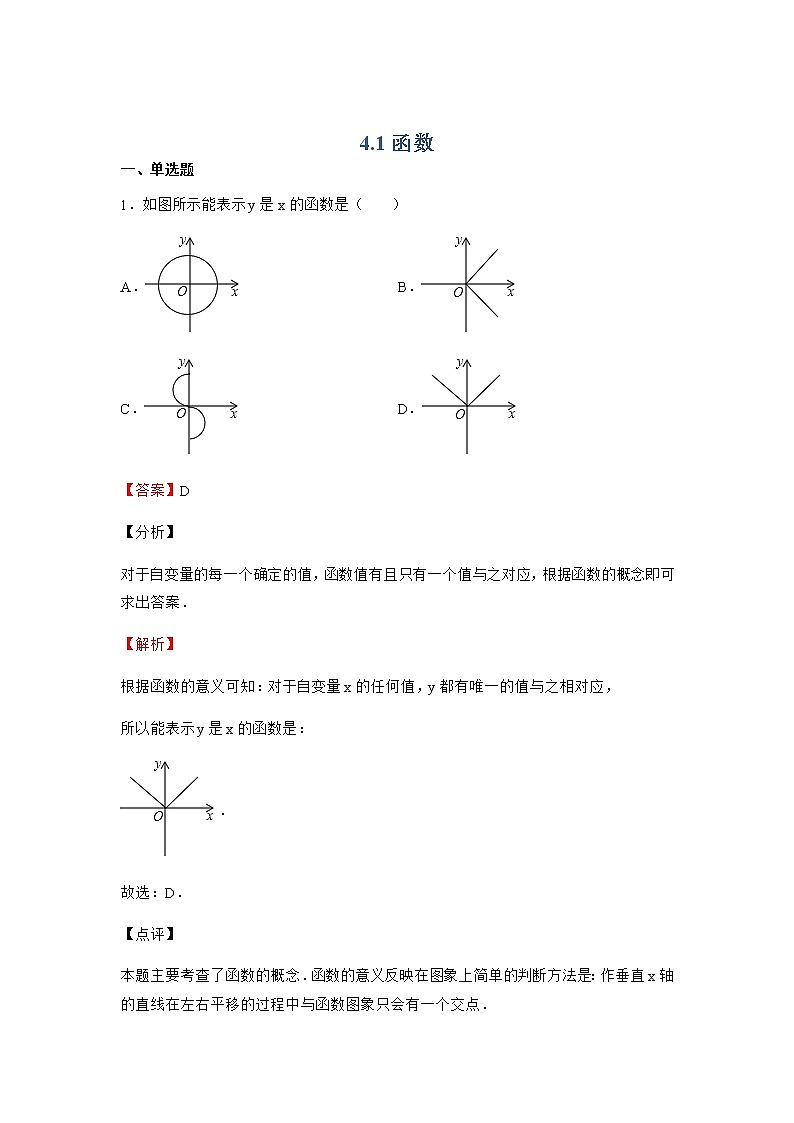
1.如图所示能表示y是x的函数是( )
A. B.
C. D.
【答案】D
【分析】
对于自变量的每一个确定的值,函数值有且只有一个值与之对应,根据函数的概念即可求出答案.
【解析】
根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,
所以能表示y是x的函数是:
.
故选:D.
【点评】
本题主要考查了函数的概念.函数的意义反映在图象上简单的判断方法是:作垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.
2.下列变量之间的关系中,是函数关系的有( ).
(1)三角形的面积与底边长;(2)多边形的内角和与边数;(3)圆的面积与半径;(4)y=2020x+365中y与x.
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】
根据函数的定义可知,对于x的每一个取值,y都有唯一的值与之对应,据此可以确定函数的个数.
【解析】
解:根据函数的定义可知:
(1)中三角形面积=底×高的一半,底和高有两个变量,不是函数;
(2)多边形的内角和=(边数-2)×180°,是函数;
(3)圆的面积=π×半径的平方,是函数;
(4)满足;故(2)/(3)/(4)是函数,(1)不是.
故选C.
【点睛】
本题考查函数的定义,需要注意几个点:①函数中有两个变量,一个是自变量,一个是因变量;②因变量会随着自变量的变化而变化;③对于自变量的每一个确定的值,因变量都有唯一的值和它对应.
3.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】
解:变量有:②行驶时间、③行驶路程、④汽车油箱中的剩余油量.共3个.
故选C.
【点睛】
本题考查变量的概念,变量是指变化的量.
4.函数y=+中自变量x的取值范围是()
A. B.且 C.且 D.
【答案】C
【分析】
根据被开方数是非负数,分母不能为零,可得不等式组,根据解不等式组,可得答案.
【解析】
解:由题意,得,
解得x≤3且x≠2,
故选C.
【点睛】
本题考查了函数自变量的取值范围,利用被开方数是非负数,分母不能为零得出不等式组是解题关键.
5.下面关于函数的三种表示方法叙述错误的是()
A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值
C.用公式法表示函数关系,可以方便地计算函数值
D.任何函数关系都可以用上述三种方法来表示
【答案】D
【分析】
根据函数的表示方法的优缺点分析解答即可.
【解析】
A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化,此选项正确;
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值,此选项正确;
C.用公式法表示函数关系,可以方便地计算函数值,此选项正确;
D.并不是任何函数关系都可以用上述三种方法来表示,此选项错误.
故选:D.
【点睛】
本题考查函数的表示方法,明确三种表示方法的特点是解题的关键.
6.下列有序实数对中,是函数y=2x-1中自变量x与函数值y的一对对应值的是( )
A.(-2.5,4)
B.(-0.25,0.5)
C.(1,3)
D.(2.5,4)
【答案】D
【分析】
在四个坐标中,把坐标中的x或y代入,对照所得的y或x值与坐标值是否相同即得到判断.
【解析】
A、代入y=4,则x=2.5,错误,故本选项不符;
B、代入y=0.5,则x=0.75,错误,故本选项不符;
C、代入x=1,则y=1,错误,故本选项不符;
D、代入y=4,x=2.5,正确,故本选项符合.
故选D.
【点睛】
本题考查了函数值的一一对应,把坐标中的横坐标或纵坐标代入进行对照是否相同即可.
7.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量
【答案】D
【分析】
根据函数的定义:对于函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应;来解答即可.
【解析】
在这个问题中,x是自变量,y是因变量,0.6元/千瓦时是常数.
故选:D.
【点评】
本题考查了函数的定义:设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,称变量y为变量x的函数,记作y=f(x);变量是指在程序的运行过程中随时可以发生变化的量.
8.某科研小组在网上获取了声音在空气中传播的速度与空气温度的关系的一些数据(如下表):
气温 | ||||||
声速 |
下列说法正确的是()
A.在这个变化中,自变量是声速,因变量是气温
B.温度越高,声速越慢
C.当气温为时,声音可以传播
D.气温每升高,声速减小
【答案】C
【分析】
根据自变量、因变量的含义,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【解析】
∵在这个变化中,自变量是气温,因变量是声速,
∴选项错误;
∵根据数据表,可得温度越高,声速越快,
∴选项错误;
∵,
∴当气温为时,声音可以传播,
∴选项正确;
∵,,
,,
∴当温度每升高,声速增加,
∴选项错误.
故选:C.
【点睛】
本题主要考查了自变量、因变量的含义和判断.熟练掌握自变量、因变量的含义是解题的关键.
9.我们知道,在弹性限度内,弹簧挂上重物后会伸长.已知一根弹簧的长度与所挂重物的质量之间的关系如下表,则下列说法错误的是()
重物的质量 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
A.在这一变化过程中,重物的质量是自变量,弹簧的长度是因变量
B.当所挂重物的质量是时,弹簧的长度是
C.在弹性限度内,当所挂重物的质量是时,弹簧的长度是
D.当不挂重物时,弹簧的长度应为
【答案】C
【分析】
根据表格数据可得与成一次函数关系,设,取两点代入可得出与的关系式,进而分析得出答案.
【解析】
解:由表格可得:随的增大而增大;在这一变化过程中,重物的质量是自变量,弹簧的长度是因变量,故选项正确,不合题意;
设,
将点,代入可得:,
解得:.
故,
当时,,故选项正确,不合题意;
当时,,故选项错误,符合题意;
当时,,即弹簧不挂物体时的长度是,故选项正确,不合题意.
故选:.
【点睛】
本题考查了函数关系式及函数值的知识,解答本题的关键是观察表格中的数据,得出y与x的函数关系式.
10.从某容器口以均匀的速度注入酒精,若液面高度h随时间t的变化情况如右图所示,则对应容器的形状应为()
A. B. C. D.
【答案】C
【分析】
根据题意先比较函数图象几段的变化快慢,再比较四个容器容积各部分的大小,即可得出图形.
【解析】
根据图象可知,容器底部比较粗,然后逐渐变细,然后又逐渐变粗,最后又变得细,并且最后非常细,推断可能是C容器.
故选:C
【点睛】
本题考查利用函数的图象解决实际问题,正确理解函数的图象所表示的意义是解题的关键,注意容器粗细和水面高度变化的关系.
二、填空题
11.对于圆的周长公式c=2πr,其中自变量是______,因变量是______.
【答案】rc
【解析】
试题解析:∵圆的周长随着圆的半径的变化而变化,
∴对于圆的周长公式,其中自变量是,因变量是 .
故答案为
12.表示函数的三种方法是:________,________,________.
【答案】列表法解析式法图象法
【分析】
根据函数的三种表示方法:列表法、解析式法、图象法.进行填空即可.
【解析】
解:表示函数的三种方法是:列表法、解析式法、图象法.
故答案为:列表法;解析式法;图象法.
【点睛】
此题主要考查函数的表示方法,解题的关键是熟知函数的三种方法是:列表法、解析式法、图象法.
13.在下列关系式中:①长方形的宽一定时,其长与面积的关系;②等腰三角形的底边长与面积;③圆的周长与圆的半径.其中,是函数关系的是________(填序号)
【答案】①③
【分析】
根据函数定义:对于函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,解答即可.
【解析】
①长面积宽,是函数关系;
②高不能确定,共有三个变量,不是函数关系;
③周长半径,是函数关系.
故答案为:①③.
【点评】
本题主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
14.将写成用的代数式表示的形式为______,那么______是______的函数,______是自变量.
【答案】
【分析】
根据等式的性质将等式表示成左边为b右边为含a的代数式的形式即可,根据函数的定义填写后面三个空.
【解析】
解:∵
移项可得:
将b的系数化为1得:.
根据函数的定义b是a的函数,a是自变量,b是因变量
故四个空依次填:,b,a,a.
【点睛】
等式的性质和函数的定义.在用的代数式表示时可将a看成已知数,b看成未知数,解b的方程即可,理解函数的定义也是解决本题的关键.
15.某种储蓄月利率是0.36%,今存入本金100元,则本息和(元)与所存月数(个)之间的函数解析式是______.
【答案】
【分析】
根据本金、利息和时间之间的关系,利息=本金×月利率×月数,本息和=本金+利息,即可得出答案.
【解析】
根据题意,y=100+100×0.36%×x=0.36x+100.
故填.
【点睛】
本题考查用关系式法表示变量之间的关系.能理清题意找出本金、利息和时间之间的关系是解决此题的关键.
16.嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的支笔,还买了单价为5元的三角尺两幅,用(元)表示琪琪花的总钱数,那么与之间的关系式应该是______________.
【答案】
【分析】
先求得每支笔的价格,然后依据总售价=单价×支数列出关于即可.
【解析】
解:∵每支笔的价格=9÷6=1.5元/支,
∴y与x之间的关系式为:y=1.5x+5×2,
即:y=1.5x+10,
故答案为:y=1.5x+10.
【点睛】
本题主要考查的是列函数关系式,掌握题目中的数量关系是解题的关键.
17.如图(a)所示,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,的面积为y,如果y关于x的关系如图(b)所示,则m的值是________.
【答案】5
【分析】
先根据点(2,3)在图象上得出BC的长,然后利用三角形的面积求出AB的长,进而可得答案.
【解析】
解:由图象上的点可知:,
由三角形面积公式,得:,解得:.
,.
故答案为:5.
【点睛】
本题考查了利用图象表示变量之间的关系,属于常见题型,根据题意和图象得出BC和AB的长是解题关键.
18.某城市大剧院地面的一部分为扇形观众席的座位按表所示的方式设置:
排数 | 1 | 2 | 3 | 4 | …… |
座位数 | 50 | 53 | 56 | 59 | …… |
则第六排有________个座位;第n排有________个座位
【答案】65
【分析】
从具体数据中,不难发现:后一排总比前一排多3,由此求得第六排的座位,根据此规律,第n排有50+3(n-1)个,再化简即可.
【解析】
解:第6排有62+3=65个座位,
第n排有50+3(n-1)=3n+47个座位.
故答案为:65,3n+47.
【点睛】
本题考查列代数式,找出座位数排列规律是解决问题的关键.
19.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时) | 0 | 1 | 2 | 3 |
y(升) | 100 | 92 | 84 | 76 |
由表格中y与t的关系可知,当汽车行驶________小时,油箱的余油量为0.
【答案】12.5
【分析】
由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少8L,据此可得y与t的关系式.
【解析】
解:由题意可得:y=100-8t,
当y=0时,0=100-8t
解得:t=12.5.
故答案为:12.5.
【点睛】
本题考查函数关系式.注意贮满100L汽油的汽车,最多行驶的时间就是油箱中剩余油量为0时的t的值.
20.如图所示的程序是一种数值转换程序,当输入的x值为1.5时,输出的y值为________.
【答案】0.5
【分析】
先根据x的取值确定x的范围,从而得出需要代入的函数关系式,然后代入计算即可.
【解析】
解:因为x=1.5满足:,所以把x=1.5代入,得:.
故答案为:0.5.
【点睛】
本题考查了用关系式表示变量之间的关系以及因变量的求值,属于常见题型,读懂题意、弄清需要代入的函数关系式是解题关键.
三、解答题
21.已知函数.
(1)求自变量等于5时的函数值;
(2)求函数值等于5时的自变量值.
【答案】(1)6;(2)或.
【分析】
(1)直接利用代入求出答案;
(2)直接利用代入求出答案.
【解析】
解:(1)当时,;
(2)当时,,
解得:或.
【点睛】
此题主要考查了函数值,正确理解题意代入正确数据是解题关键.
22.下表是某报纸公布的世界人口数据情况:
年份 | 1957 | 1974 | 1987 | 1999 | 2010 |
人口数 | 30亿 | 40亿 | 50亿 | 60亿 | 70亿 |
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口数那么随着x的变化,y的变化趋势是怎样的?
【答案】(1)两个变量;(2)用x表示年份,用y表示世界人口数,那么随着x的变化,y的变化趋势是增大.
【分析】
(1)年份和人口数都在变化,据此得到;
(2)根据人口的变化写出变化趋势即可;
【解析】
解:(1)表中有两个变量,分别是年份和人口数;
(2)用表示年份,用表示世界人口总数,那么随着的变化,的变化趋势是增大.
【点睛】
本题考查了变量与常量的知识,解题的关键是能够了解常量与变量的定义,难度不大.
23.某河流受暴雨影响,水位不断上涨,下面是某天此河流的水位记录:
时间(时) | 0 | 4 | 8 | 12 | 16 | 20 | 24 |
水位(米) | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 |
(1)上表反映的是哪两个量之间的关系?自变量和因变量各是什么?
(2)根据表格画了表示两个变量的折线统计图.
(3)哪段时间水位上升得最快?
【答案】(1)时间和水位之间的关系,时间是自变量,水位是因变量;(2)见解析;(3)20-24水位上升最快.
【解析】
【分析】
(1)根据表格可知是时间和水位之间的关系,在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中水位随时间的变化记录画图;
(3)相同的时间上升的水位越多代表上升的越快,根据此规律看表数据即可判断.
【解析】
解:(1)根据表格可知是时间和水位之间的关系,并且每过4个小时水位在变化,可知水位随着时间在变化,即时间是自变量,水位是因变量;
(2)见下图:
(3)0-4时的变化情况为2.5-2=0.5m;
4-8时的变化情况为3-2.5=0.5m;
8-12时的变化情况为4-3=1m;
12-16时的变化情况为5-4=1m;
16-20时的变化情况为6-5=1m;
20-24时的变化情况为8-6=2m;
∴20-24水位上升最快.
【点睛】
考查水位变化情况和频率分布折线图,解题的关键是能够读懂表格,并作出折线统计图,难度不大.
24.杨师傅开车从A地出发去300千米远的B地游玩,其行驶路程s与时间t之间的关系如图所示,出发一段时间后,汽车发生故障,需停车检修,修好后又继续行驶.根据题意回答下列问题:
(1)上述问题中反映的是哪两个变量之间的关系?并指出自变量和因变量;
(2)汽车停车检修了多长时间?修车的地方离B地还有多远?
(3)车修好后每小时走多少千米?
【答案】(1)上述问题中反映的是行驶路程与行驶时间的关系;自变量是行驶时间,因变量是行驶路程.(2)汽车停车检修了1小时;修车的地方离B地还有150千米.(3)车修好后每小时走75千米.
【分析】
(1)根据函数的图象可以知道横轴表示时间,纵轴表示路程,据此可以得到答案;
(2)观察图象可以得到汽车在3-4小时之间路程没有增加,说明此时在检修,由B地或C地的纵坐标即可得出答案;
(3)检修后两小时走了150千米据此可以求得速度.
【解析】
解:(1)上述问题中反映的是行驶路程与行驶时间的关系;
自变量是行驶时间,因变量是行驶路程.
(2),,
∴汽车停车检修了1小时;修车的地方离B地还有150千米.
(3)(300-150)÷(6-4)=75(千米/小时)
答:车修好后每小时走75千米.
【点睛】
此题主要考查了看函数图象,解此类问题时,首先要看清横纵坐标所表示的意义.
25.某种车的油箱加满油后,油箱中的剩余油量y(升)与车行驶路程x(千米)之间的关系,如图所示,根据图象回答下列问题:
(1)这种车的油箱最多能装 升油.
(2)加满油后可供该车行驶 千米.
(3)该车每行驶200千米消耗汽油 升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶 千米后,车辆将自动报警?
【答案】(1)50;(2)1000;(3)10;(4)800
【分析】
(1)当x=0时,y的值就是这种车的油箱的最大容量;
(2)当y=0时,x的值就是该车行驶的行驶里程;
(3)观察图象可知,该车每行驶200千米消耗汽油10升;
(4)观察图象可知,行驶800千米后,车辆将自动报警.
【解析】
解:(1)这种车的油箱最多能装50升油.
(2)加满油后可供该车行驶1000千米.
(3)该车每行驶200千米消耗汽油10升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶800千米后,车辆将自动报警.
故答案为:(1)50;(2)1000;(3)10;(4)800.
【点睛】
此题主要考查了函数的图象,从一次函数的图象上获取正确的信息是解题关键.
26.心理学家发现,学生对概念的接受能力与提出概念所用的时间(单位:分)之间有如下关系:(其中)
提出概念所用时间 | |||||||||
对概念的接受能力 |
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念所用时间为几分钟时,学生的接受能力最强?
(4)从表中可知,当时间在什么范围内,学生的接受能力逐步增强?当时间在什么范围内,学生的接受能力逐步降低?
【答案】(1)提出概念所用的时间和对概念的接受能力两个变量之间的关系,提出概念所用时间是自变量,对概念的接受能力是因变量;(2);(3)提出概念所用时间为分钟时,学生的接受能力最强;(3)当时,值逐渐增大,学生的接受能力逐步增强;当时,值逐渐减小,学生的接受能力逐步降低
【分析】
(1)根据自变量与因变量的定义即可求解;
(2)根据表格中数据即可求解;
(3)根据表格中时,的值最大是,即可求解;
(4)根据表格中的数据即可求解.
【解析】
解:提出概念所用的时间和对概念的接受能力两个变量;
提出概念所用时间是自变量,对概念的接受能力是因变量.
当时,,
所以当提出概念所用时间是分钟时,学生的接受能力是.
当时,的值最大是,所以提出概念所用时间为分钟时,学生的接受能力最强.
由表中数据可知:当时,值逐渐增大,学生的接受能力逐步增强;当时,值逐渐减小,学生的接受能力逐步降低.
【点睛】
准确理解函数的概念:在运动变化过程中有两个变量和,对于的每一个值,都有唯一确定的值与之对应,是的函数,是自变量.
初中数学北师大版八年级上册第四章 一次函数1 函数练习题: 这是一份初中数学北师大版八年级上册第四章 一次函数1 函数练习题,共8页。
初中第四章 一次函数1 函数优秀当堂检测题: 这是一份初中第四章 一次函数1 函数优秀当堂检测题,共7页。试卷主要包含了1 函数》同步练习,函数的自变量x的取值范围是等内容,欢迎下载使用。
初中数学北师大版八年级上册1 函数精品课时训练: 这是一份初中数学北师大版八年级上册1 函数精品课时训练,共13页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













