第16章一次函数评估测试卷

(时间：120分钟　满分：120分)

一、选择题(下列各题的备选答案中，只有一个答案是正确的，每小题2分，共20分)

1．直线y＝kx－1一定经过点(　A　)

A．(0，－1)   B．(1,0) 

C．(0，k)   D．(1，k)

2．函数y＝2x，y＝－3x，y＝－x的共同特点是(　D　)

A．图象位于同样的象限   B．y随x的增大而减小

C．y随x的增大而增大   D．图象都过原点

3．对于一次函数y＝－2x＋4，下列结论错误的是(　D　)

A．函数值随自变量的增大而减小

B．函数的图象不经过第三象限

C．函数的图象向下平移4个单位长度得y＝－2x的图象

D．函数的图象与x轴的交点坐标是(0,4)

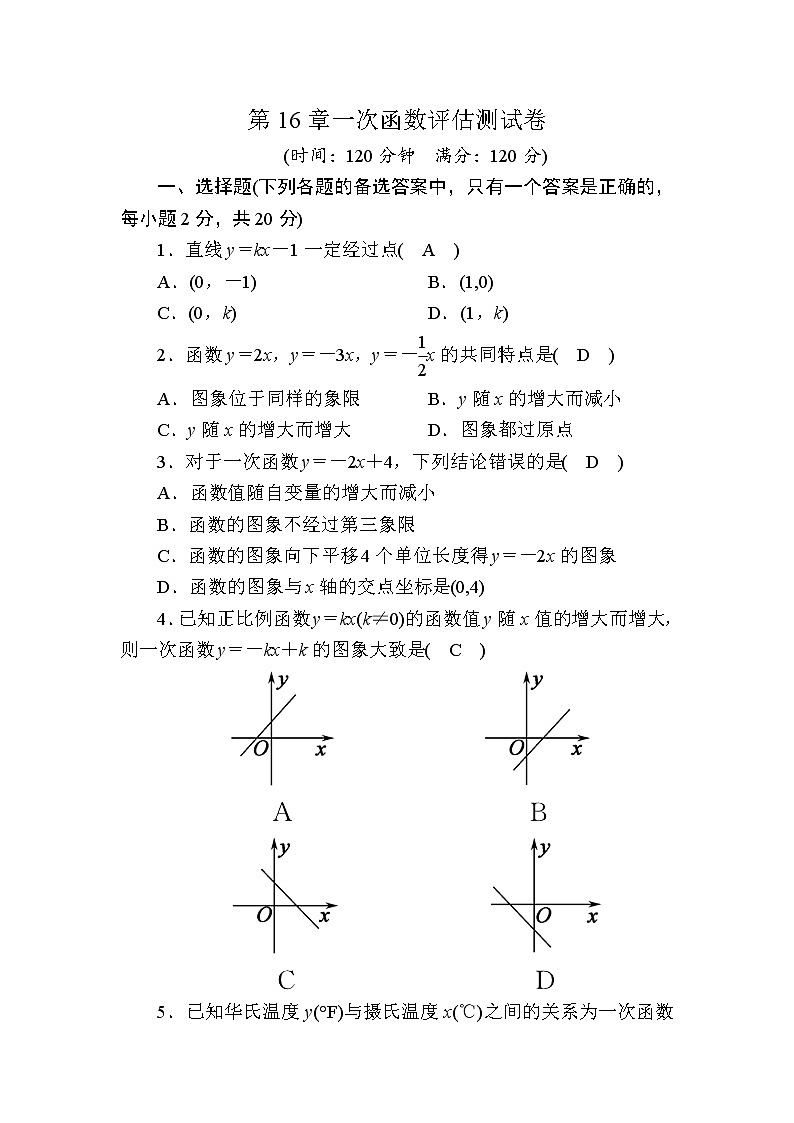
4．已知正比例函数y＝kx(k≠0)的函数值y随x值的增大而增大，则一次函数y＝－kx＋k的图象大致是(　C　)

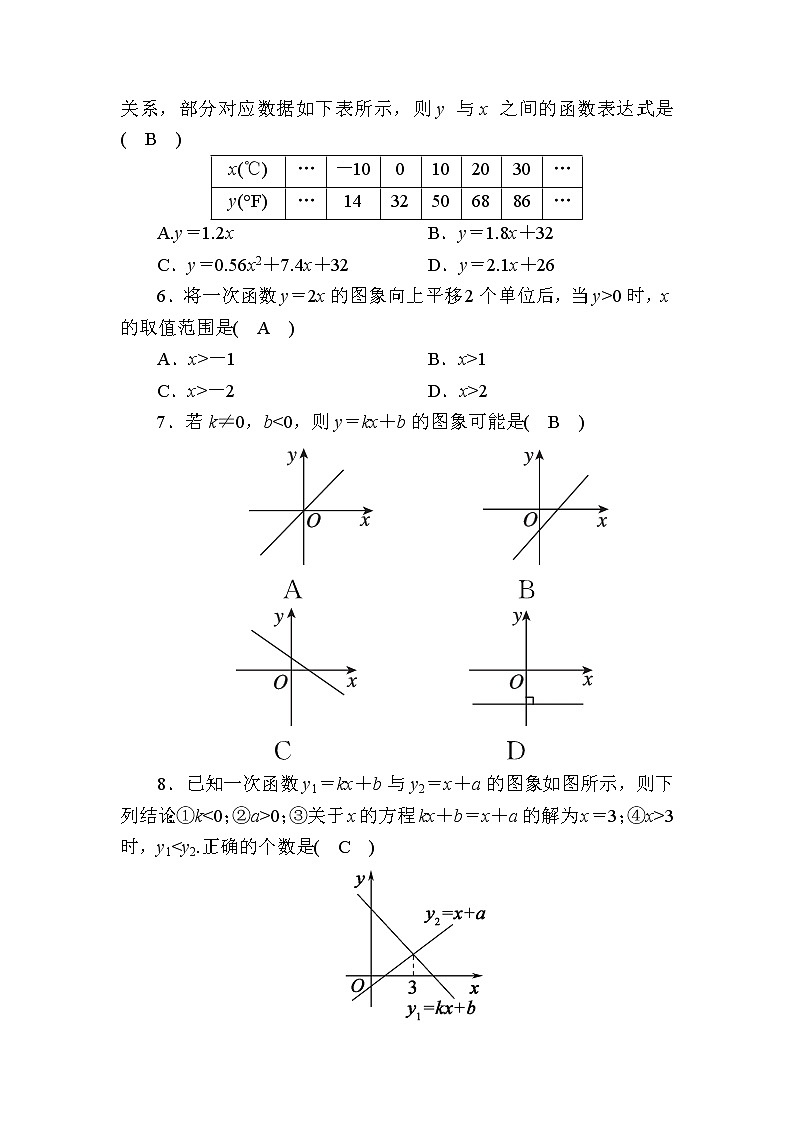
5．已知华氏温度y(°F)与摄氏温度x(℃)之间的关系为一次函数关系，部分对应数据如下表所示，则y与x之间的函数表达式是(　B　)

A.y＝1.2x   B．y＝1.8x＋32

C．y＝0.56x2＋7.4x＋32   D．y＝2.1x＋26

6．将一次函数y＝2x的图象向上平移2个单位后，当y>0时，x的取值范围是(　A　)

A．x>－1   B．x>1  

C．x>－2    D．x>2

7．若k≠0，b<0，则y＝kx＋b的图象可能是(　B　)

8．已知一次函数y1＝kx＋b与y2＝x＋a的图象如图所示，则下列结论：①k<0；②a>0；③关于x的方程kx＋b＝x＋a的解为x＝3；④x>3时，y1<y2.正确的个数是(　C　)

A．1   B．2

C．3   D．4

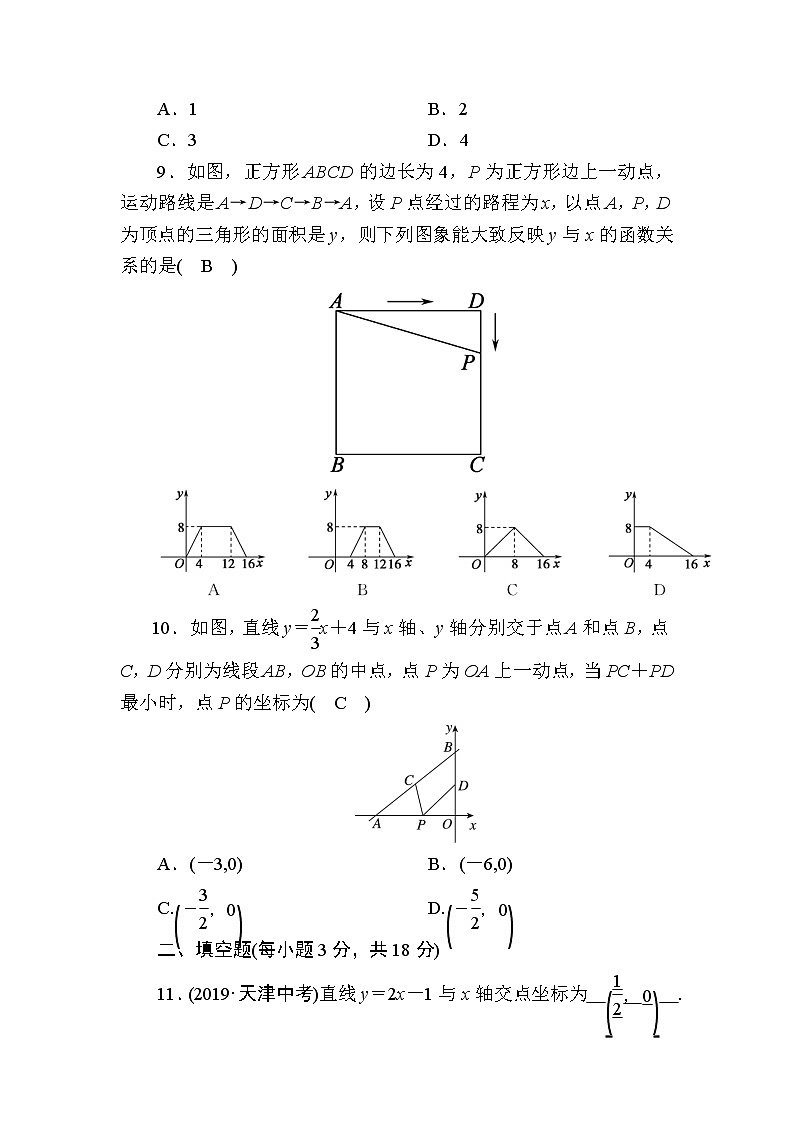
9．如图，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是A→D→C→B→A，设P点经过的路程为x，以点A，P，D为顶点的三角形的面积是y，则下列图象能大致反映y与x的函数关系的是(　B　)

10．如图，直线y＝x＋4与x轴、y轴分别交于点A和点B，点C，D分别为线段AB，OB的中点，点P为OA上一动点，当PC＋PD最小时，点P的坐标为(　C　)

A．(－3,0)   B．(－6,0) 

C.   D.

二、填空题(每小题3分，共18分)

11．(2019·天津中考)直线y＝2x－1与x轴交点坐标为　　.

12．小明根据某个一次函数表达式填写了下表，其中有一格不慎被墨汁遮住了，根据表格的规律找出空格里原来填的数是__2__.

13.在平面直角坐标系中，已知一次函数y＝－2x＋1的图象经过P1(x1，y1)，P2(x2，y2)两点，若x1<x2，则y1__>__y2(填“>”“<”或“＝”)．

14．函数y＝－x＋8的图象与x轴的交点A的坐标为__(12,0)__，与y轴的交点B的坐标为__(0,8)__，与两坐标轴围成的三角形的面积是__48__.

15．如图，一次函数y＝kx＋b(k≠0)的图象与正比例函数y＝2x的图象平行且经过点A(1，－2)，则kb＝__－8__.

16．如图，已知直线y＝ax＋b，则方程ax＋b＝2的解为x＝__3__.

　　　　　　　　 　 　第16题图

三、解答题(第17小题6分，第18、19小题各8分，共22分)

17．(2020·大连模拟)如图，一次函数y＝－x＋m的图象与y轴交于点B，与正比例函数y＝x的图象交于点P(2，n)．

(1)求m和n的值；

(2)求△POB的面积．

解：(1)因为点P(2，n)在函数y＝x的图象上，所以n＝×2＝3，所以点P的坐标为(2,3)．把P(2,3)代入y＝－x＋m.得3＝－2＋m，所以m＝5.

(2)由(1)知，一次函数的表达式为y＝－x＋5，令x＝0，得y＝5，所以点B的坐标为(0,5)，

所以S△POB＝×5×2＝5.

18．已知一次函数y＝(m－2)x－3m2＋12，问：

(1)当m为何值时，函数图象过原点？

(2)当m为何值时，函数图象平行于直线y＝2x?

解：(1)因为一次函数的图象经过原点，所以－3m2＋12＝0且m－2≠0，所以m＝－2.

(2)因为函数图象平行于直线y＝2x，所以m－2＝2，解得m＝4.

19．从甲地到乙地的公路长约240 km，骑自行车以每小时20 km的速度从甲地出发，t h后离乙地s km.

(1)写出s与t的函数关系式；

(2)画出这个函数的图象；

(3)8 h后距乙地多远？出发后几小时，到两地的距离相等？

解：(1)s＝240－20t(0≤t≤12)．

(2)列表：

图象如图所示．

(3)把t＝8代入s＝240－20t，得s＝80.

把s＝120代入s＝240－20t，得t＝6.

所以8 h后距乙地80 km，出发后6 h，到两地的距离相等．

四、(每小题8分，共16分)

20．直线y＝－2x＋4与x轴交于点A，与y轴交于点B，直线y＝kx＋b(k，b是常数，k≠0)经过点A，与y轴交于点C，且OC＝OA.

(1)求点A的坐标及k的值；

(2)已知点C在x轴的上方，点P在直线y＝－2x＋4上，若PC＝PB，求点P的坐标．

解：(1)由题意，知直线y＝－2x＋4与x轴交于点A，令y＝0，则－2x＋4＝0，解得x＝2，所以A(2,0)，所以OA＝2.因为点C在y轴上，且OC＝OA，所以C(0,2)或C(0，－2)，因为直线y＝kx＋b(k，b是常数，k≠0)经过点A和点C，所以或解得k＝1或k＝－1.

(2)因为点C在x轴的上方，所以C(0,2)．因为B为直线y＝－2x＋4与y轴的交点，所以B(0,4)．

因为B(0,4)，C(0,2)，PC＝PB，所以点P的纵坐标为3.

又因为点P在直线y＝－2x＋4上，把y＝3代入y＝－2x＋4，解得x＝，所以P.

21．如图，已知直线l1：y＝2x－7与直线l2：y＝－x＋交于点A，直线l1、直线l2分别交y轴于点B，C，求△ABC的面积．

解：由2x－7＝－x＋，得x＝3，将x＝3代入y＝2x－7得，y＝－1，所以A(3，－1)，又可得B(0，－7)，C，所以BC＝－(－7)＝，所以S△ABC＝××3＝.

五、(本题10分)

22．如图，直线y＝－x＋10与x轴、y轴分别交于点B，C，点A的坐标为(8,0)，点P(xP，yP)是直线y＝－x＋10在第一象限内的一个动点．

(1)求△OPA的面积S与xP之间的函数关系式，并写出xP的取值范围；

(2)当△OPA的面积为10时，求点P的坐标．

解：(1)因为A(8,0)，所以OA＝8，

所以S＝OA·|yP|＝×8×(－xP＋10)＝－4xP＋40(0＜xP＜10)．

(2)当S＝10时，－4xP＋40＝10，所以xP＝，当xP＝时，yP＝－＋10＝，

所以当△OPA的面积为10时，点P的坐标为.

六、(本题10分)

23．如图，直线y＝－2x＋8与两坐标轴分别交于P，Q两点，在线段PQ上取一点A，过点A作长方形ABOC，使点B在x轴上，点C在y轴上，若长方形ABOC的周长为14，求点A，B，C的坐标．

解：因为点A在线段PQ上，所以可设点A的坐标为(m，－2m＋8)．

由题意知P(4,0)，Q(0,8)．

因为点A在线段PQ上，所以0≤m≤4.

因为长方形ABOC的周长为14，

所以2[m＋(－2m＋8)]＝14，

解得m＝1，所以－2m＋8＝－2×1＋8＝6，

所以点A的坐标为(1,6)．

因为点B，C分别在x轴、y轴上，

所以点B的坐标为(1,0)，点C的坐标为(0,6)．

七、(本题12分)

24．在一条笔直的公路旁依次有A，B，C三个村庄，甲、乙两人同时分别从A，B两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向C村，最终到达C村．设甲、乙两人到C村的距离y1，y2(km)与行驶时间x(h)之间的函数关系如图所示，请回答下列问题：

(1)A，C两村间的距离为__120__km，a＝__2__；

(2)求出图中点P的坐标，并解释该点坐标所表示的实际意义；

(3)乙在行驶过程中，何时距甲10 km?

解：(2)设y1＝k1x＋120(k1≠0)，代入(2,0)，解得y1＝－60x＋120，

设y2＝k2x＋90(k2≠0)，代入(3,0)，解得y1＝－30x＋90，

由－60x＋120＝－30x＋90，解得x＝1，则y1＝y2＝60，

所以P(1,60)，表示经过1 h甲与乙相遇且距C村60 km.

(3)当y1－y2＝10时，即－60x＋120－(－30x＋90)＝10，解得x＝；

当y2－y1＝10时，即－30x＋90－(－60x＋120)＝10，解得x＝；

当甲走到C地，而乙距离C地10 km时，即－30x＋90＝10，解得x＝；

综上可知：当x＝ h，或x＝ h，或x＝ h时，乙距甲10 km.

八、(本题12分)

25．甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9 h，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量分别为y甲，y乙(件)，甲车间加工的时间为x(h)，y甲，y乙与x之间的函数图象如图所示．

(1)甲车间每小时加工服装__80__件，这批服装共有__1_140__件；

(2)求乙车间维修设备后，其加工服装的数量y乙与x之间的函数关系式；

(3)求甲、乙两车间共同加工完1 000件服装时甲车间所用的时间．

解：(2)乙车间每小时加工服装120÷2＝60(件)，

乙车间从开始加工到修好设备所用的时间为9－(420－120)÷60＝4(h)．

所以乙车间维修设备后，其加工服装的数量y乙与x之间的函数关系式为y乙＝120＋60(x－4)＝60x－120(4≤x≤9)．

(3)由已知可得，甲车间加工服装数量，y甲与x之间的函数关系式为y甲＝80x，显然甲、乙两车间共同加工完1 000件服装应在乙车间维修设备之后，则y甲＋y乙＝1 000，即80x＋60x－120＝1 000，解得x＝8.

故甲、乙两车间共同加工完1 000件服装时，甲车间所用的时间为8 h.