










数学七年级下册5.2.2 平行线的判定精品课件ppt
展开人教版数学七年级下册
5.2.2 《平行线的判定1》教案
课题名 | 5.2.2 《平行线的判定1》 | ||
教学目标 | 1. 探索两直线平行的条件. 2. 理解“同位角相等,两条直线平行”. | ||
教学重点 | 同位角相等,两条直线平行. | ||
教学难点 | 运用平行线的判定方法进行简单的推理. | ||
教学准备 | 教师准备:直尺、三角板 学生准备:直尺、三角板 | ||
教学过程 | |||
教学流程 | 教师活动 | 学生活动 | 设计意图 |
新课导入 | 出示课件,展示预习题
提问,简单讲解。
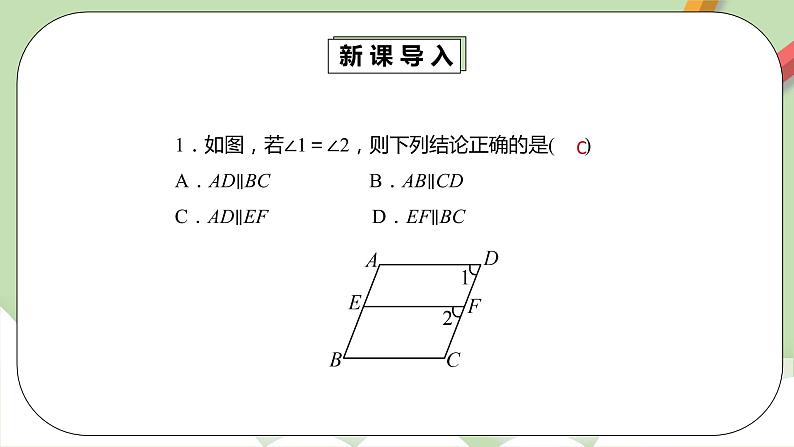
如何判断两条直线是否平行? 1.根据平行线的定义:如果平面内的两条直线不相交,就可以判断这两条直线平行. 2.根据平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行. | 【课前预习】 如果∠1=∠2,∠2=∠5,∠3=∠4能判定哪两条直线平行? 【预习检测】 1.如图,若∠1=∠2,则下列结论正确的是( ) A.AD∥BC B.AB∥CD C.AD∥EF D.EF∥BC 2.如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( ) A.∠2=35° B.∠2=45° C.∠2=55° D.∠2=125°
思考并回答老师的提问,学生可根据目前所掌握的知识,列举出来和平行有关的知识点,来回答老师的问题。 | 有目的预习以利及时发现探究重点,并引入新课。
引导学生思考还有没有其他的判定方法。引出新知。
|
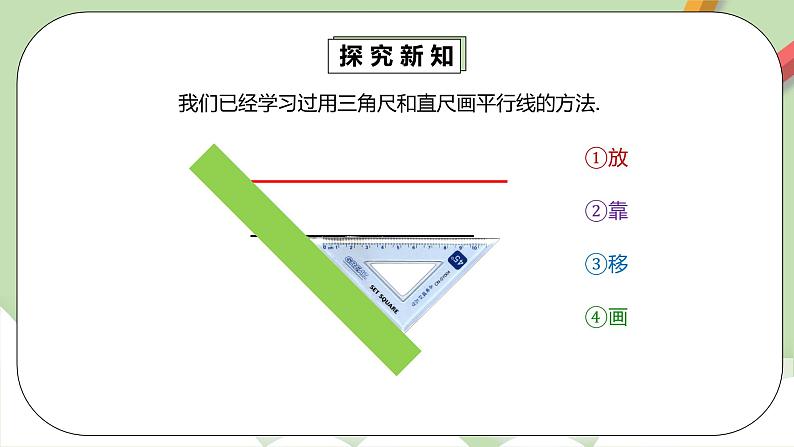
探究新知 | 复习画两条平行线的方法 提问:(1)怎样用语言叙述上面的图形? (2)画图过程中,什么角始终保持相等? (3)直线l1,l2位置关系如何? (4)可以叙述为:____________________________. 4.平行线的判定方法1 由上面,同学们你能发现判定两直线平行的方法吗? 语言叙述: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 几何叙述: ∵∠1=∠2 (已知), ∴l1∥l2 (同位角相等,两直线平行). | 学生回忆: 放、靠、移、画的步骤
发现同一个三角板同一个角与“同位角”建立联系。 | 把基本的事实与几何上的位置关系、数量关系建立联系。
直观表象帮助学生建立新知模型,形成脑图。
培养学生素养,人书写习惯开始;学会用数学语言表达证明步骤。 归纳总结探究的结果。
|
典例剖析 | 例1 下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推理过程. | ||
方法提炼 | |||
典例剖析 | 例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
| ||
方法提炼 | 判断两条直线是否平行,可以找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行. | ||
跟踪训练 | 问题:如图,你能说出木工用图中,这种叫做角尺的工具画平行线的道理吗? 如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB_____CD. | ||
链接中考 | (河池中考)如图,∠1=120°,要使a∥b,则∠2的大小是( ) A.60° B.80° C.100° D.120° | ||
随堂检测 | 1.如图是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( ) A.同位角相等,两直线平行 B.内错角相等,两直线平行 C.两直线平行,同位角相等 D.两直线平行,内错角相等 2.三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( ) A.a⊥b B.a∥b C.a⊥b或a∥b D.无法确定 3.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( ) A.AD∥BC B.AB∥CD C.CA平分∠BCD D.AC平分∠BAD 4.如图,已知AB⊥BD于点B,CD⊥BD于点D,∠1=∠2,试问CD与EF平行吗?为什么? 解:CD∥EF.理由如下: 因为∠1=∠2(__________), 所以AB∥EF (_______________________________________). 因为AB⊥BD,CD⊥BD,所以AB∥CD (_______________________________________________). 所以CD∥EF (_______________________________). 5.用一副三角尺拼图,并标点描线如图所示,然后过点C作CF平分∠DCE,交DE于点F.试说明CF∥AB. 6.如图,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F.问:CE与DF的位置关系怎样?试说明理由. | ||
课堂小结 | |||
教学反思 | 一堂课下来,也有遗憾。比如一个提问的不到位,上台展示的学生误解了我的意思,竟去书写推证过程(这超出了他们此时的能力范围)。在这堂课上,部分同学没有展示自己的勇气,我没有顾及到,在今后的教学中应更有激情和爱心。而本节课对初一学生而言,本是又一个艰难的起步。但这一堂课,学生学得比较轻松,课后作业效果也很好,基本达到“轻负荷,高质量”的教学要求。 | ||
【预习检测】
1.答案:C
2.答案:C
【链接中考】
答案:D
【随堂检测】
1.答案:A
2.答案:B
3.答案:B
4.答案:已知;
同位角相等,两直线平行;
在同一平面内,垂直于同一条直线的两条直线平行;
平行于同一条直线的两条直线平行
5.解:因为CF平分∠DCE,且∠DCE=90°,
所以∠DCF=∠DCE=×90°=45°.
因为∠ABC=45°,
所以∠ABC=∠DCF.
所以CF∥AB.
6.解:CE∥DF.
理由如下:
因为BD平分∠ABC,CE平分∠ACB,
所以∠DBC=∠ABC,∠ECB=∠ACB.
又因为∠ABC=∠ACB,所以∠DBC=∠ECB.
又因为∠DBF=∠F,所以∠ECB=∠F.
所以CE∥DF.
初中数学人教版七年级下册5.2.2 平行线的判定一等奖课件ppt: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c88528_t3/?tag_id=26" target="_blank">5.2.2 平行线的判定一等奖课件ppt</a>,共37页。PPT课件主要包含了温故知新,素养目标,课堂导入,新知探究,跟踪练习,还有其他解法吗,课堂小结,∠1∠2,∠3∠2,∠2+∠4180°等内容,欢迎下载使用。
人教版七年级下册5.2.2 平行线的判定完美版ppt课件: 这是一份人教版七年级下册5.2.2 平行线的判定完美版ppt课件,文件包含522平行线的判定pptx、522平行线的判定导学案doc、522平行线的判定教案doc等3份课件配套教学资源,其中PPT共54页, 欢迎下载使用。
初中数学5.2.2 平行线的判定获奖ppt课件: 这是一份初中数学5.2.2 平行线的判定获奖ppt课件,文件包含522第1课时平行线的判定1pptx、RJ中学数学七年级下522平行线的判定第二课时教学详案docx等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。














