人教版七年级下册5.3.1 平行线的性质优质课件ppt

课题名

5.3.1平行线的性质

教学目标

1．掌握平行线的性质，会运用两条直线是平行关系判断角相等或互补．

2．能够根据平行线的性质进行简单的推理．

教学重点

探索并掌握平行线的性质，能用平行线的性质进行简单的推理和计算．

教学难点

能区分平行线的性质和判定，以及平行线的判定和性质的综合运用．

教学准备

教师准备：PPT、卡纸、直尺、三角板、圆规

学生准备：卡纸、直尺、三角板、圆规剪刀

教学过程

教学流程

教师活动

学生活动

设计意图

新课导入

师：出示检测题：

已知∠1=70°，∠2=70°，∠3=70°．求∠4的度数．

解：∵∠1=70°，∠2=70° (________________)

∴∠_________=∠_________

∴_________ (__________________)

∴_________＋_________=180°(_____________________________)

∴∠4=180°－∠_________=180°－_________＝_________

师出示幻灯片，引入新课。

根据右图，填空：

① 如果∠1＝∠C，

那么________∥_________ (                         )

② 如果∠1＝∠B

那么 _________∥_________ (                        )

③ 如果∠2＋∠B＝180°，

那么 _________∥_________ (                         )

同学们，前面我们知道了利用同位角相等，内错角相等，同旁内角互补，可以判定两条直线平行，反过来，如果两条直线平行，它们所得到的同位角、内错角和同旁内角又各有什么关系呢？我们一起来探究吧！

解答预习检测题，由小组长向老师反馈答题情况。

逆向思考，把平行的判定定理逆向叙述应该是怎样的一种表达呢？

既然同位角相等、内错角相等和同旁内角互补可以判断两直线平行，那么反过来思考：

两直线平行，可不可以判定同位角相等、内错角相等和同旁内角互补呢？

检测预习情况

培养逆向思考能力，并引入新课。

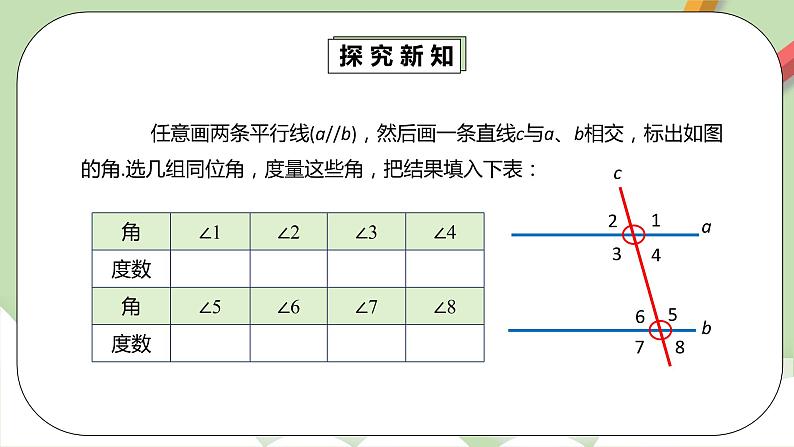
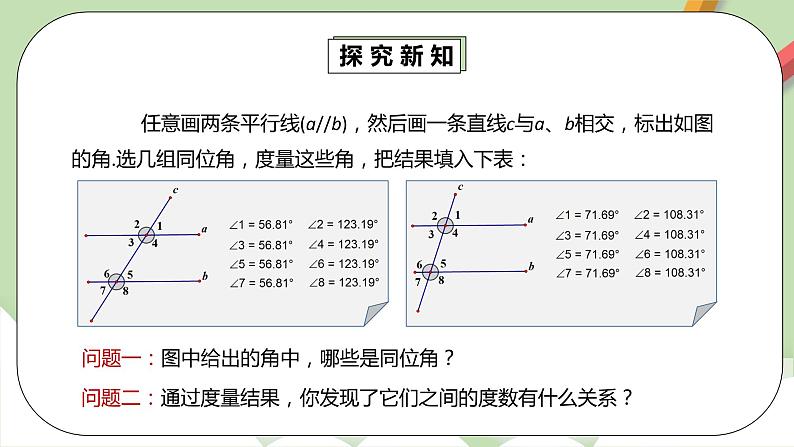
探究新知

任意画两条平行线(a//b)，然后画一条直线c与a、b相交，标出如图的角.选几组同位角，度量这些角，把结果填入下表：

问题一：图中给出的角中，哪些是同位角？

问题二：通过度量结果，你发现了它们之间的度数有什么关系？

问题三：改变直线c的位置，平行线之间的同位角关系还存在吗?

问题四：猜想两条平行线被第三条直线所截得的同位角有什么关系吗？

    1．(1)猜想：上节课我们利用“同位角、内错角、同旁内角”其中某一组之间的等量关系判定“两条直线”位置关系．反过来已知“两条直线平行”的位置关系，“同位角”有什么大小关系？写出你的猜想：____________________________________.

(2)测量：自研教材P18的探究，动手，通过测量完成P18的填空，再任意画一条截线d，并度量各角的度数，比较同位角：∠1_______∠5；∠2_______∠6；∠3_______∠7；∠4_______∠8．

(3)归纳：

如果______________ (线的位置关系)，那么______________ (角的大小关系)．

2．结合右边的图形，用几何语言表示平行线的性质1：

________________________________________________________________

自研教材P19的“思考”，根据“思考”完成下面的探究：

1．上面已经学习了“两直线平行，同位角相等，”，结合P19思考内容，你猜想两直线平行，内错角、同旁内角各有怎样的关系？

内错角的关系：_____________________________

同旁内角的关系：_____________________________

2．你能用“两直线平行，同位角相等”来分别验证以上两个猜想吗？

3．总结归纳平行线的性质．

【性质应用】

自研教材P19的例题，思考：

四边形ABCD是梯形，隐含的条件为：_________；所以∠A与∠D_________，∠B与_________互补，于是：∠D=_________；∠C=_________．本题用到了平行线的性质是：______________________________．

学生用直尺、三角板画出任意平行线，通过实践操作，得出正确结论。

通过同位角、内错角和同旁内角的度数的对比，得出性质定理。

“两直线平行，同位角相等。”

得出两直线平行，同位角相等。

几何语言：

∵ a∥b (已知)

∴ ∠1=∠2 (两直线平行，同位角相等)

得出“两直线平行，内错角相等。”

得出：“两直线平行，同旁内角互补。

明确探究范围，强调“相交”。

直观表象帮助学生建立新知模型，形成脑图。

学会用数学语言表达证明步骤。

归纳总结探究的结果。

归纳总结探究的结果，学会用几何语言表达推理过程。

跟踪训练

如图，已知平行线AB、CD被直线AE所截.

(1)从 ∠1=110o可以知道∠2 是多少度吗，为什么？

(2)从∠1=110o可以知道 ∠3是多少度吗，为什么？

(3)从 ∠1=110o可以知道∠4 是多少度吗，为什么？

解：(1)∠2=110o 

            ∵两直线平行，内错角相等；

(2)∠3=110o 

∵两直线平行，同位角相等；

(3) ∠4=70o

∵两直线平行，同旁内角互补.

方法提炼

链接中考

(中考·滨州) 如图，直线AB∥CD，则下列结论正确的是(　　)

A．∠1＝∠2                         B．∠3＝∠4

C．∠1＋∠3＝180°           D．∠3＋∠4＝180°

随堂检测

1．如图，，，，则∠C的度数是(    )

A．        B．          C．          D．

2．如图，直线?，?被?，?所截，且?//?，则下列结论中正确的是(    )

A．∠1=∠2     B．∠3=∠4      C．∠2+∠4=180°        D．∠1+∠4=180°

3．(1)有这样一道题：如图1，若AB∥DE，AC∥DF，试说明∠A=∠D．请补全下面的解答过程，括号内填写依据．

解：∵AB∥DE (              )

∴∠A=_______ (                           )

∵AC∥DF (           )

∴∠D=______ (                           )

∴∠A=∠D (                  )

(2)有这样一道题：如图2，若AB∥DE，AC∥DF，试说明∠A+∠D=180°．请补全下面的解答过程，括号内填写依据．

解：∵AB∥DE(                   )

∴∠A=_____(                       )

∵AC∥DF(         )

∴∠D+ _______=180°(                          )

∴∠A+∠D=180°(                )

4．如图，潜望镜中的两面镜子是互相平行放置的，光线经过镜子反射时，∠1=∠2，∠3=∠4，∠2和∠3有什么关系？为什么进入潜望镜的光线和离开潜望镜的光线是平行的？

课堂小结

平行线的“判定”与“性质”有什么不同？

判定：已知角的关系得平行的关系．

      推平行，用判定．

性质：已知平行的关系得角的关系．

      知平行，用性质．

教学反思

数学教学是数学活动的教学，通过数学活动让学生掌握知识，在学生活动的过程中体现师生的交往、互动与共同发展。如要真正掌握平行线的性质必然先要学会它的应用，在此我设计了三个层次的例题:直接应用型;先判定后应用型;判定性质混合型。直接应用型侧重学生符号语言的规范表达，复杂类型的例题侧重对学生证明思路和方法上的引导，这两方面都是几何学习中的重点和难点。我先从一个简单的图形出发，对图形和条件作一定的改变，考察学生对知识的理解和掌握。同时，数学学习离不开练习和反馈，小结完成后进行目标检测，检查学生知识掌握情况。