新疆维吾尔自治区乌鲁木齐市新市区第十五中学2022-2023学年九年级上学期期中考试数学试卷 （含答案）

2022-2023学年乌鲁木齐市第十五中学九年级上学期期中考试

数学试卷

满分：150分  考试时间：120分钟

注意事项：

1．答题前填写好自己的姓名、班级、考号等信息

2．请将答案正确填写在答题卡上

第I卷（选择题）

一、单选题(每小题5分，共45分)

1．下列方程中，是关于的一元二次方程的是（    ）

A． B．

C． D．

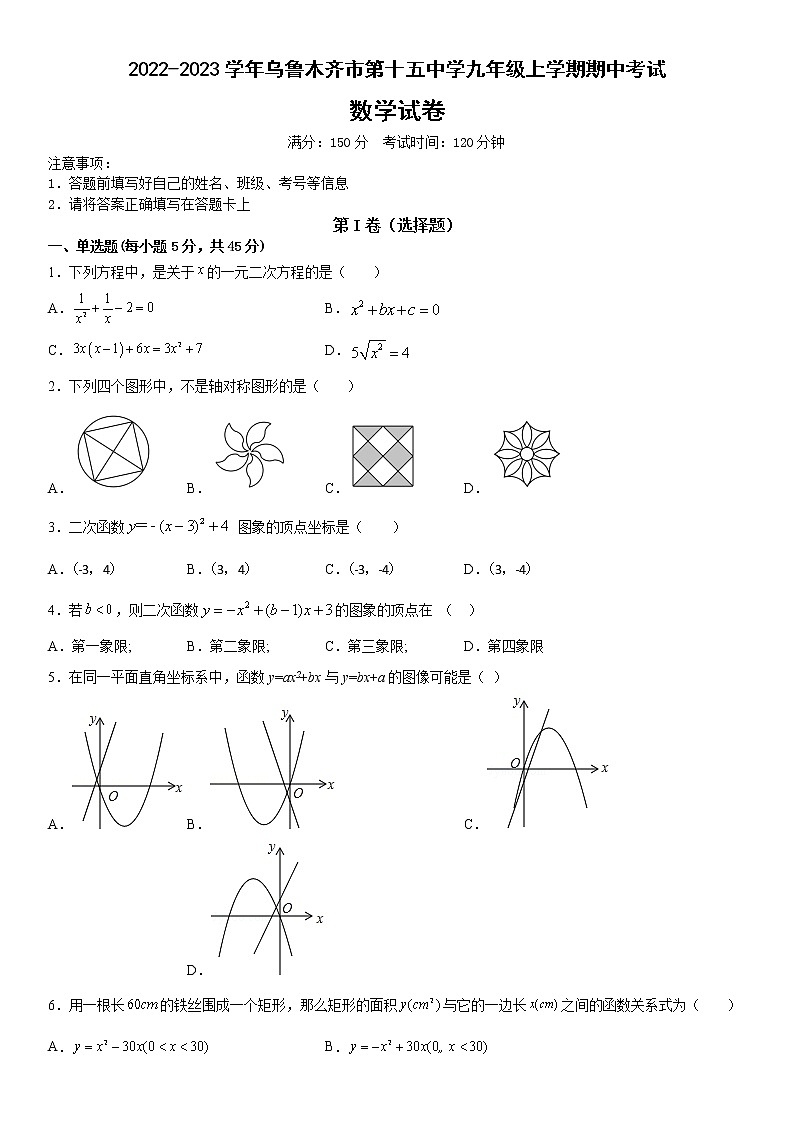
2．下列四个图形中，不是轴对称图形的是（    ）

A． B． C． D．

3．二次函数 图象的顶点坐标是（　　）

A．（﹣3，4） B．（3，4） C．（﹣3，﹣4） D．（3，﹣4）

4．若，则二次函数的图象的顶点在 （  ）

A．第一象限; B．第二象限; C．第三象限; D．第四象限

5．在同一平面直角坐标系中，函数y=ax2+bx与y=bx+a的图像可能是（ ）

A． B． C． D．

6．用一根长的铁丝围成一个矩形，那么矩形的面积与它的一边长之间的函数关系式为（    ）

A． B．

C． D．

7．如图，点A为⊙O上一点，如果，那么半径的长是（    ）

A． B．2 C．1 D．3

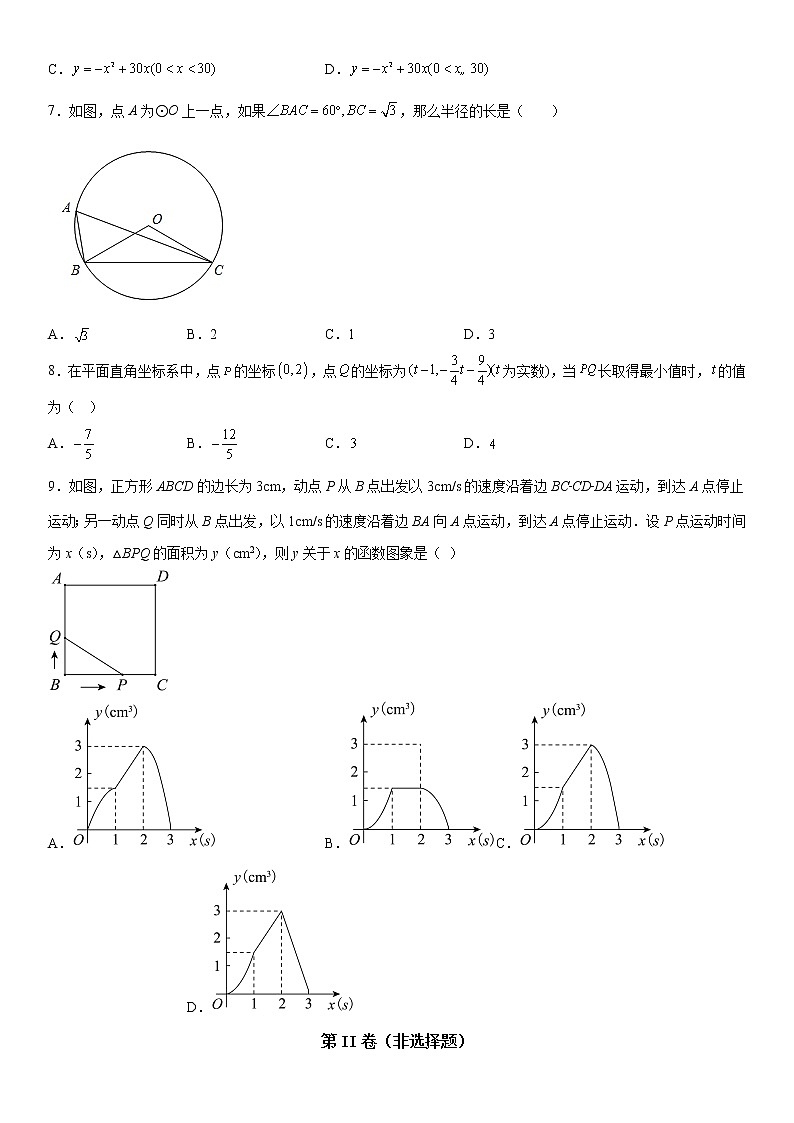
8．在平面直角坐标系中，点的坐标，点的坐标为为实数)，当长取得最小值时，的值为（  ）

A． B． C． D．

9．如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动，到达A点停止运动；另一动点Q同时从B点出发，以1cm/s的速度沿着边BA向A点运动，到达A点停止运动．设P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函数图象是（ ）

A． B． C． D．

第II卷（非选择题）

二、填空题(每小题5分，共30分)

10．直线 上有一点P（2，m），则P点关于原点的对称点的坐标为_________．

11．将抛物线 向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为___________________．

12．如图，△ABC绕点A顺时针方向旋转45°得到△，若∠BAC=90°，AB=AC=，则图中阴影部分的面积等于_______．

13．若关于x的函数与x轴仅有一个公共点，则实数k的值为___

14．半径为的圆中有一条弦长为的弦，那么这条弦所对的圆周角的度数等于_________.

15．已知二次函数为常数)，当时，的最大值是，则的值是__________．

三、解答题(共75分)

16．（8分）解方程：

 (1)

(2)

17．（8分）农民张大伯为了致富奔小康，大力发展家庭养殖业，他准备用40米长的木栏围一个矩形的养圈，为了节约材料，同时要使矩形面积最大，他利用了自己家房屋一面长25米的墙，设计了如图一个矩形的养圈．

（1）请你求出张大伯设计的矩形羊圈的面积；

（2）请你判断他的设计方案是否使矩形羊圈的面积最大？如果不是最大，应怎样设计？请说明理由．

18．（8分）如图，王强在一次高尔夫球的练习中，在某处击球，其飞行路线满足抛物线，其中（m）是球的飞行高度，（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．

（1）请写出抛物线的开口方向、顶点坐标、对称轴．

（2）请求出球飞行的最大水平距离．

（3）若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球飞行路线应满足怎样的抛物线，求出其解析式

19．（8分）已知中，边及边上的高的和为．

请直接写出的面积与边的长之间的函数关系式(不要求写出自变量的取值范围)；

当是多少时，这个三角形面积最大？最大面积是多少？

20．（8分）某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：．

（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？

（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？

（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？

（成本＝进价×销售量）

21．（10分）某文具店销售A、B两种文具，其中A文具的定价为20元/件，B产品的定价10元/件．

（1）若该文具按定价售出A、B两种文具共400件，若销售总额不低于5000元，则至少销售A产品多少件？

（2）该文具店2018年2月按定价销售A文具280件，B文具120件，2018年3月，市场情况发生变化，A文具销售价与上个月持平，但这个月的销售量比上个月减少了m%；B文具的销售价比上个月减少了m%，但销售量增加了m%；3月份的销售总金额与2月份保持不变．求m的值．

22．（12分）如图，内接于，过点C作的切线，交AB延长线于点D，于点E，交CD于点F．

(1)求证；

(2)若 ，AC＝8，求圆O的半径．

23．（13分）定义: 在平面直角坐标系中，如果点和都在某函数的图象上，则称点是图象的一对“相关点”．例如，点和点是直线的一对相关点．

请写出反比例函数的图象上的一对相关点的坐标；

如图，抛物线的对称轴为直线，与轴交于点．

求抛物线的解析式:

若点是抛物线上的一对相关点，直线与轴交于点，点为抛物线上之间的一点，求面积的最大值．

参考答案：

1．B

2．B

3．B

4．C

5．C

6．C

7．C

8．A

9．C

10．（-2，-7）．

11．

12．

13．0或-1

14．或．

15．和

16．（1）  ， ；

（2） .

17．（1）由题意可得张大伯设计羊圈的面积为：

S=25×7.5=187.5（平方米），

答：张大伯设计羊圈的面积为187.5平方米．

（2）不是最大．

设矩形的长为x，面积为y，

∴当x=20时y最大=200，

此时矩形的长为20米，宽为10米．

18．（1）抛物线开口向下，顶点为（4，），对称轴为x＝4；

（2）球飞行的最大水平距离是8m；

（3）

19．（1）；

（2）当为时，三角形面积最大，最大面积是

20．（1）35元

（2）销售单价应定为30元或40元

（3）3600元

21．（1）100件；

（2）m=15.

22．(1)证明：

(2)5

23．（1），；

（2）①；

②