新疆乌鲁木齐市第四十四中学2021-2022学年九年级上学期期中考试数学试卷　（含答案）

这是一份新疆乌鲁木齐市第四十四中学2021-2022学年九年级上学期期中考试数学试卷　（含答案），共7页。试卷主要包含了请将答案正确填写在答题卡上，用配方法解方 ，配方后可得，由二次函数可知，把一副三角板等内容，欢迎下载使用。
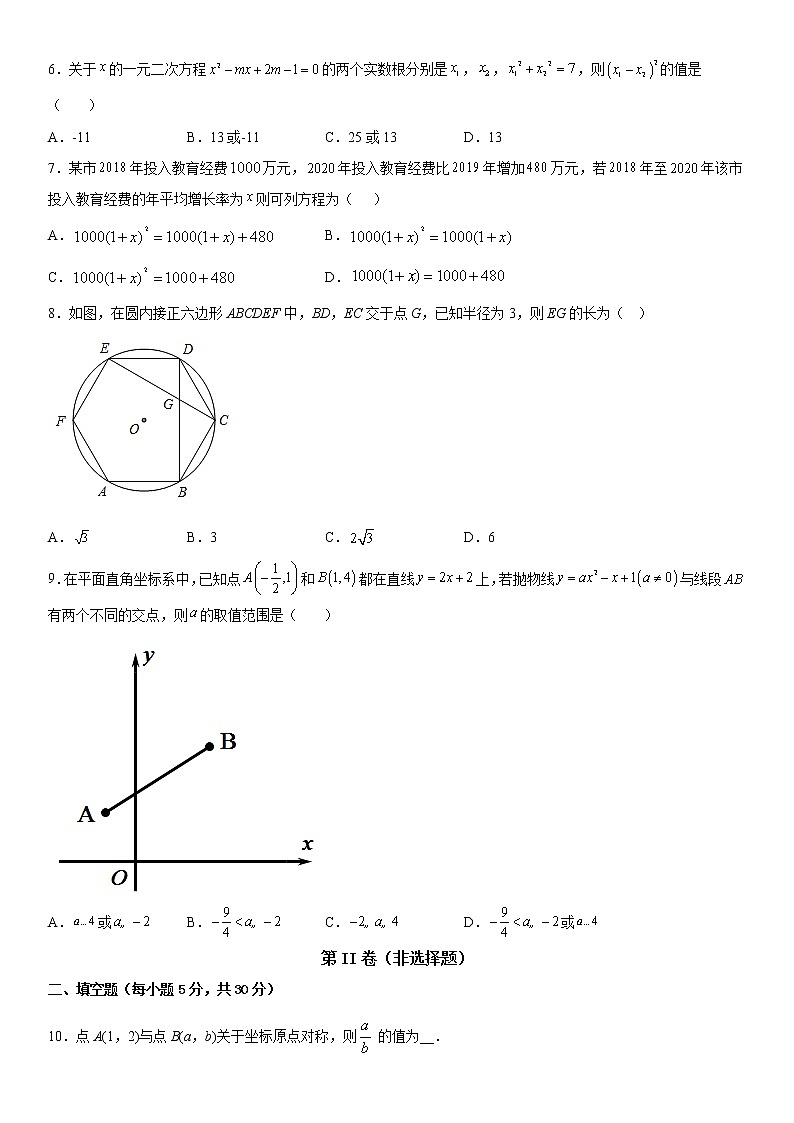
2021-2022学年乌鲁木齐市第44中学九年级上学期期中考试数学试卷满分：150分   考试时间：120分钟注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第I卷（选择题）一、单选题（每小题5分，共45分）1．若关于的一元二次方程有一个根为0，则的值是（    ）A． B． C． D．或2．下列图形中既是轴对称图形又是中心对称图形的是（　　）A． B． C． D．3．用配方法解方 ，配方后可得（   ）A． B． C． D． 4．由二次函数可知（    ）A．图象开口向上 B．图象向右平移1个单位得到C．图象的对称轴为直线 D．当时，y随x的增大而增大5．把一副三角板（如图甲）放置，其中∠ACB＝∠DEC＝90°，∠A＝45°，∠D＝30°，斜边AB＝6cm，DC＝cm，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），这时AB与CD1相交于点O，与D1E1相交于点F，则线段AD1的长为（　　）A．5cm B．5cm C．17cm D．cm6．关于的一元二次方程的两个实数根分别是，，，则的值是（    ）A．-11 B．13或-11 C．25或13 D．137．某市年投入教育经费万元，年投入教育经费比年增加万元，若年至年该市投入教育经费的年平均增长率为则可列方程为（   ）A． B．C． D．8．如图，在圆内接正六边形ABCDEF中，BD，EC交于点G，已知半径为3，则EG的长为（  ）A． B．3 C． D．69．在平面直角坐标系中，已知点和都在直线上，若抛物线与线段有两个不同的交点，则的取值范围是（    ）A．或 B． C． D．或第II卷（非选择题）二、填空题（每小题5分，共30分）10．点A(1，2)与点B(a，b)关于坐标原点对称，则 的值为__．11．将抛物线向右平移1个单位，再向下平移1个单位，那么得到的抛物线的解析式为______．12．已知等腰三角形的两边长分别为a，b，若，且a，b均是方程的解，则这个三角形的周长为___________.13．设，是一个直角三角形两条直角边的长，且，则这个直角三角形的外接圆面积为__________．14．有一个抛物线形的立交桥拱，这个桥拱的最大高度为16m，跨度为40m．现将它的图形放在坐标系里（如图所示）．若在离跨度中心M点10m处垂直竖立一铁柱支撑拱顶，这铁柱长______米．15．如图和中，，，，点在边上，将绕点按每秒的速度沿顺时针方向旋转一周，在旋转的过程中当∥时，旋转时间_____秒．三、解答题（共75分）16．（8分）解方程： (1)(2)17．（8分）已知关于x的方程．(1)求证：无论m取何值，该方程总有实数根；(2)若方程的两个根都是整数，请写出一个满足条件的m的值，并求出此时方程的根．18．（8分）如图，△ABC绕着顶点A逆时针旋转到△ADE，∠B＝40°，∠E＝60°，AB//DE，求∠DAC的度数．19．（8分）如图，在中，，，点P从点A开始沿边向终点B以的速度移动，点Q从点B开始沿边向终点C以的速度移动．如果P、Q分别从A、B同时出发，点Q运动到终点C时整个运动过程结束．(1)____________秒后，的面积等于？(2)_________秒后，的长度等于？(3)的面积能否等于？说明理由．20．（8分）如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃．设垂直于墙的一面篱笆长为x米，花圃的总面积为S平方米．(1)若围成花圃的总面积为20平方米，请设计方案．(2)求S关于x的函数关系式，并求出最大面积．21．（10分）某宾馆有60个房间供游客住宿，当每个房间的房价为每天200元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房空闲，宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于380元．设每个房间的房价每天增加元（为10的正整数倍）．(1)设一天订住的房间数为，直接写出与的函数关系式及自变量的取值的范围；(2)设宾馆一天的利润为元，求与的函数关系式；(3)一天订住多少个房时，宾馆的利润最大?最大利润是多少元．22．（12分）如图，是的直径，点C在的延长线上，平分交于点D，且，垂足为点E．(1)判断直线与的位置关系，并说明理由；(2)若，，求半径的长．23．（13分）如图1，抛物线，交轴于A、B两点，交轴于点，为抛物线顶点，直线垂直于轴于点，当时，．(1)求抛物线的表达式；(2)点是线段上的动点（除、外），过点作轴的垂线交抛物线于点．①当点的横坐标为2时，求四边形的面积；②如图2，直线，分别与抛物线对称轴交于、两点．试问，是否为定值？如果是，请求出这个定值；如果不是，请说明理由．
参考答案：1．A2．B3．B4．B5．D6．D7．A8．C9．D10．11． 12．1513．14．1215．11或2916． (1)，(2)，17．(1)(2)时，方程的两根为，18．40°19．(1)1(2)2(3)不能，20．(1)围成宽为1，长20米或宽为4米，长为5米的长方形(2)，面积最大最大值为平方米21．(1)（）；(2)；(3)42；15120．22．(1)(2)6．23．(1)(2)①；②是，定值为