广东省汕头市林百欣中学2022-2023学年九年级上学期数学科期中综合素质摸查试题 (含答案)

展开

这是一份广东省汕头市林百欣中学2022-2023学年九年级上学期数学科期中综合素质摸查试题 (含答案)，共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
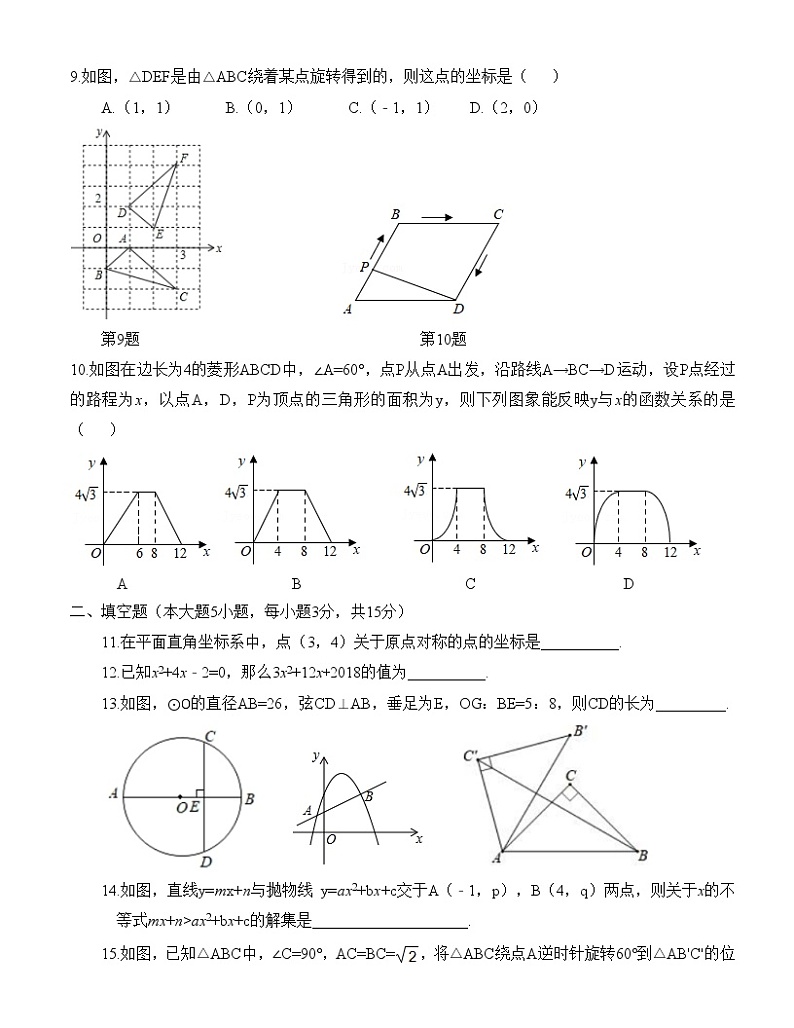
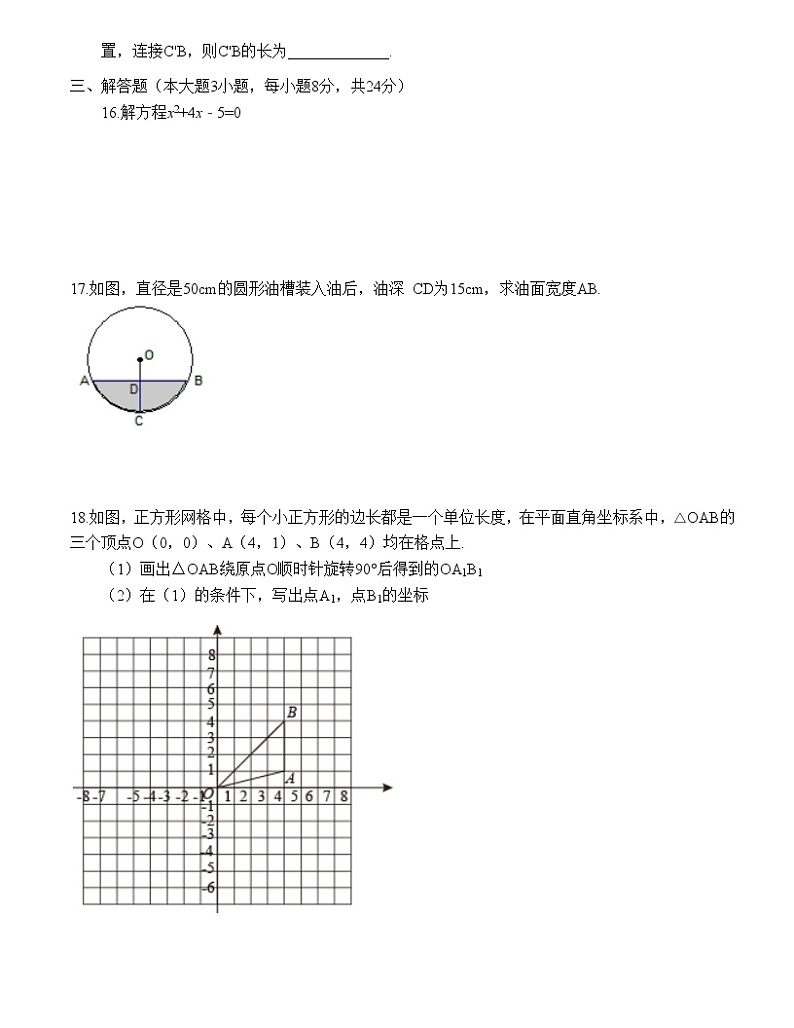
汕头市林百欣中学2022-2023学年度第一学期九年级数学科期中综合素质摸查（含答案）一、单选题（本大题10小题，每小题3分，共30分）1.下列形中，既是轴对称图形又是中心对称图形的是（）A.平行四边形 B.正五边形 C.圆 D.等边三角形2.将二次函数y=x2的图象向右平移2个单位；再向上平移1个单位，所得图象的表达式是（）A. y=(x﹣2)2 +1 B. y= (x+2)2 +1 C. y=(x﹣2)2﹣1 D. y= (x+2)2﹣13.如图，将△ABC就点C按逆时针方向旋转75°后得到△A'B'C，若∠ACB=25°则∠BCA'的度数为（）A.50° B.40° C.25° D.60° 第3题第6题第8题4.已知函数y=(x﹣1)2+2，当函数值y随x的增大而减小时，x的取值范围是（）A. x <l B. x >1 C. x >﹣2 D. ﹣2< x <45．根据下列表格的对应值：x﹣111.11.2x2+12x﹣15﹣26﹣2﹣0.590.84由此可判断方程x2+12x﹣15=0必有一个解x满足（）A. ﹣1<x< l B. 1< x <1.1 C. 1.1< x <1.2 D. ﹣0.59< x <0.846.如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，连接AE.若∠BCD=2∠BAD，则∠DAE的度数是（）A.30° B.35° C.45° D.60°7.某经济开发区，今年一月份工业产值达50亿元，第一季度总产值为175亿元，二月、三月平均每月的增长率是多少？若设平均每月的增长率为x，根据题意，可列方程为（）A.50(1+x)2=175 B.50+50(1+x)+50(1+x)2 =175C.50(1+x)+50(1+x)2=175 D.50+50(1+x)2=1758.如图，BD是⊙O的直径，点A、C在⊙O上，弧AB=弧BC，∠AOB=60°，则∠BDC度数是（）A.60° B.45° C.35° D.30° 9.如图，△DEF是由△ABC绕着某点旋转得到的，则这点的坐标是（）A.（1，1） B.（0，1） C.（﹣1，1） D.（2，0）第9题第10题10.如图在边长为4的菱形ABCD中，∠A=60°，点P从点A出发，沿路线A→BC→D运动，设P点经过的路程为x，以点A，D，P为顶点的三角形的面积为y，则下列图象能反映y与x的函数关系的是（） A B C D二、填空题（本大题5小题，每小题3分，共15分）11.在平面直角坐标系中，点（3，4）关于原点对称的点的坐标是__________.12.已知x2+4x﹣2=0，那么3x2+12x+2018的值为__________.13.如图，⊙O的直径AB=26，弦CD⊥AB，垂足为E，OG：BE=5：8，则CD的长为_________. 14.如图，直线y=mx+n与抛物线 y=ax2+bx+c交于A（﹣1，p），B（4，q）两点，则关于x的不等式mx+n>ax2+bx+c的解集是____________________.15.如图，已知△ABC中，∠C=90°，AC=BC=，将△ABC绕点A逆时针旋转60°到△AB'C'的位置，连接C'B，则C'B的长为_____________.三、解答题（本大题3小题，每小题8分，共24分）16.解方程x2+4x﹣5=0 17.如图，直径是50cm的圆形油槽装入油后，油深 CD为15cm，求油面宽度AB. 18.如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△OAB的三个顶点O（0，0）、A（4，1）、B（4，4）均在格点上.（1）画出△OAB绕原点O顺时针旋转90°后得到的OA1B1（2）在（1）的条件下，写出点A1，点B1的坐标四、解答题（本大题3小题，每小题9分，共27分）19.如图，学校要用一段长为32米的篱笆围成一个一边靠墙的矩形花圃，墙长为14米.（1）若矩形ABCD的面积为96平方米，求矩形的边AB的长.（2）要想使花圃的面积最大，AB边的长应为多少米？最大面积为多少平方米？ 20.已知关于x的一元二次方程(a+c) x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长.（1）如果x= ﹣1是方程的根，试判断△ABC的形状，并说明理由；（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由； 21.已知：如图，△ABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连结AD.（1）求证：∠DAC=∠DBA；（2）连接CD，若CD=6，BD=8，求⊙O的半径和DE的长. 五、解答题（本大题2小题，每小题12分，共24分）22.如图，△ABC和△DCE都是等边三角形.探究发现（1）△BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由；拓展运用（2）若B、C、E三点不在一条直线上，∠ADC=30°，AD=3，CD=2，求BD的长；（3）若△DCE绕点C旋转，△ABC和△DCE的边长分别为1和2，当△BCD的面积最大时，AE的长为________ 23.如图，已知直线y=x+4与x轴交于点A，与y轴交于点C，抛物线y=ax2+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x=﹣1.（1）求抛物线的表达式；（2）D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；（3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请直接写出P，Q两点的坐标；若不存在，请说明理由参考答案一、单选题（本大题10小题，每小题3分，共30分）12345678910CAAACABDBB二、填空题（本大题5小题，每小题3分，共15分）11. (﹣3, ﹣4 )12. 202413. 24 14. x＜﹣1 或 x＞415. 1+三、解答题（本大题3小题，每小题8分，共24分）16.解: (x﹣1) (x+5)=0解得x1=1，x2=﹣5 17.解:连接OA∵ 直径是50cm ∴ OA= OC= 25cm∵ CD=15cm∴.OD=OC﹣CD=10 cm∵OC⊥AB∴AD= = ∴AB= 18.(1)(2) 点A1(1, ﹣4) 点B1(4, ﹣4)四、解答题（本大题3小题，每小题9分，共27分）19. （1）解：设AB为x米，则BC=（36﹣2x）米，由题意得：x（32﹣2 x）=96.解得：x 1=4，x2=12，.∵墙长为14米，32米的篱笆，∴32﹣2x ≤14，2x <32，∴9≤ x <16，∴x =12，AB=12，答：矩形的边AB的长为12米（2）由题意得y = x（32﹣2 x）=-﹣2 x2 + 32 x =﹣2(x﹣8)2+ 128，∵9≤ x <16，且﹣2<0，故抛物线开口向下，∴当x=9时，y有最大值是126，答：AB边的长应为9米时，有最大面积，且最大面积为126平方米.20. 解：（1）△ABC是等腰三角形理由如下将x= ﹣1代入方程得a +c﹣2b+ a ﹣c=0得a =b∴△ABC是等腰三角形.（2）△ABC是直角三角形理由如下：∵根判别式△=（2b）2﹣4（a +c）（a﹣c）=4b2﹣4 a 2+4c2=4（b2﹣a 2﹣c2）=0∴b2= a 2+c2.∴△ABC是直角三角形21. （1）证明：∵BD平分∠CBA，∴ ∠CBD=∠DBA，∵∠DAC与∠CBD都是弧CD所对的圆周角，∴∠DAC=∠CBD∴∠DAC=∠DBA.（2） ∵∠CBD=∠DBA∴AD = CD=6五、解答题（本大题2小题，每小题12分，共24分）22. 解：（1）全等，理由是 ∵△ABC和△DCE都是等边三角形，∴AC = BC，DC =EC，∠ACB =∠DCE =60°∴∠ACB+ ∠ACD = ∠DCE∠ACD即∠BCD=∠ACE，在△BCD和△ACE中∴△ACE≌△BCD (SAS)（2）如图3，由（1）得：△ACE≌△BCD，∴BD = AE，∵△DCE都是等边三角形，∴∠CDE = 60°，CD = DE =2，∵∠ADC = 30°∴∠ADE = ∠ADC+∠CDE = 30° + 60° = 90°在Rt△ADE中，AD=3，DE=2，∴∴BD = （3）当CD⊥BC时，△BCD的面积最大由（1）得：△ACE≌△BCD∴AE= BD= 23.（1）解：当x =0时，y=4C (0,4)当y =0时，∵对称轴为直线x =﹣1∴设抛物线的表达式：抛物线的表达式：（2）如图作DF⊥AB于F，交AC于E∴S四边形ABCD = ∴当时，当时，（3）设P（﹣1，n）∵以A，C，P，Q为顶点的四边形是以AC为对角线的菱形∴PA= PC∴ PA2= PC2