初中数学冀教版九年级上册第26章 解直角三角形综合与测试巩固练习

这是一份初中数学冀教版九年级上册第26章 解直角三角形综合与测试巩固练习，共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

第二十六章 解直角三角形 综合复习题

一、单选题
1．（2022·河北石家庄·九年级期末）在Rt△ABC中，∠C＝90°，若AC＝6，BC＝8，则cosA的值为（　　）

A． B． C． D．
2．（2022·河北秦皇岛·九年级期末）在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，那么∠B的余弦值是（    ）
A． B． C． D．
3．（2022·河北邢台·九年级期末）在直角三角形中，各边的长度都扩大3倍，则锐角A的三角函数值
A．也扩大3倍 B．缩小为原来的
C．都不变 D．有的扩大，有的缩小
4．（2022·河北保定·九年级期末）点M(－sin60°，cos60°)关于x轴对称的点的坐标是(   )
A．(，) B．(－，－)
C．(－，) D．(－，－)
5．（2022·河北唐山·九年级期末）在中，，，则（    ）
A． B． C． D．
6．（2022·河北沧州·九年级期末）图1是第七届国际数学教育大会（ICME）的会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形．若．，则的值为（    ）

A． B． C． D．
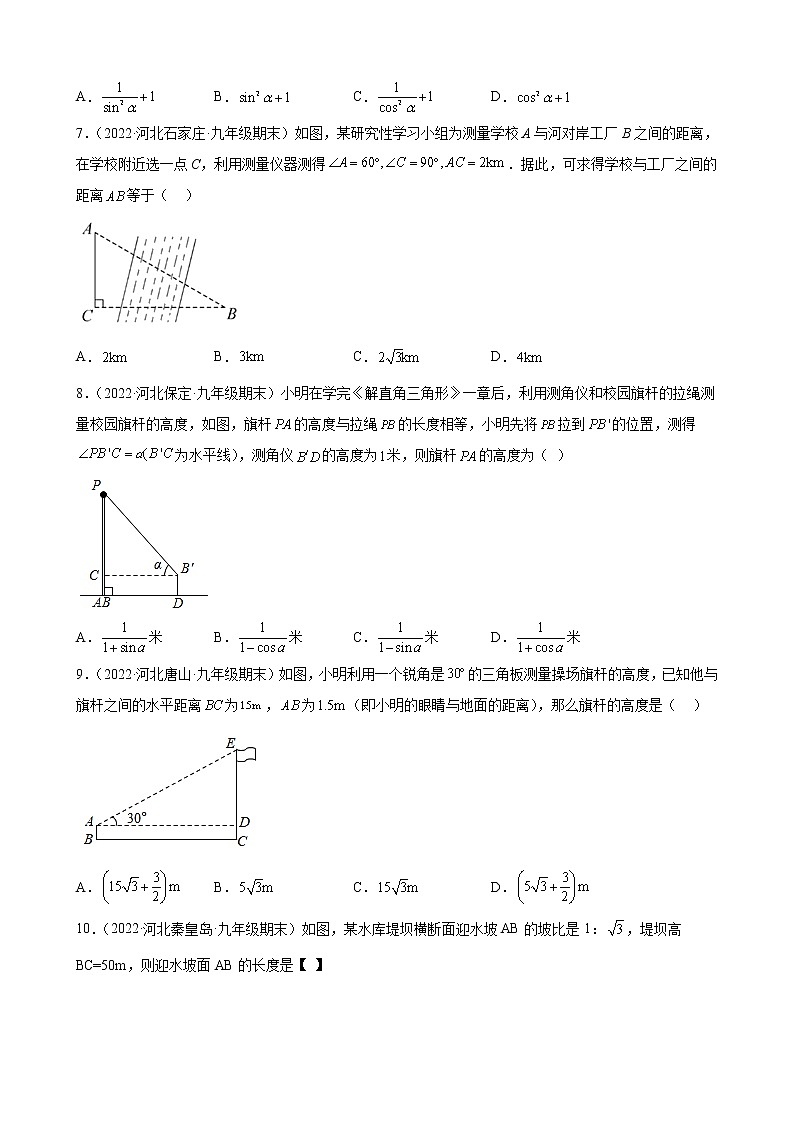
7．（2022·河北石家庄·九年级期末）如图，某研究性学习小组为测量学校A与河对岸工厂B之间的距离，在学校附近选一点C，利用测量仪器测得．据此，可求得学校与工厂之间的距离等于（    ）

A． B． C． D．
8．（2022·河北保定·九年级期末）小明在学完《解直角三角形》一章后，利用测角仪和校园旗杆的拉绳测量校园旗杆的高度，如图，旗杆的高度与拉绳的长度相等，小明先将拉到的位置，测得为水平线），测角仪的高度为米，则旗杆的高度为（  ）

A．米 B．米 C．米 D．米
9．（2022·河北唐山·九年级期末）如图，小明利用一个锐角是的三角板测量操场旗杆的高度，已知他与旗杆之间的水平距离为，为（即小明的眼睛与地面的距离），那么旗杆的高度是（    ）

A． B． C． D．
10．（2022·河北秦皇岛·九年级期末）如图，某水库堤坝横断面迎水坡AB的坡比是1：，堤坝高BC=50m，则迎水坡面AB的长度是【 】

A．100m B．100m C．150m D．50m
11．（2022·河北沧州·九年级期末）如图是东西流向且河岸平行的一段河道，点A，B分别为两岸上一点，且点B在点A正南方向，由点向正西方向走a米到达点，此时测得点在点A的南偏西方向上，则河宽的长为(   )．

A．a米 B．米 C．米 D．米

二、填空题
12．（2022·河北石家庄·九年级期末）如图，各三角形的顶点都在方格纸的格点上，则___________．

13．（2022·河北秦皇岛·九年级期末）计算：＝___．
14．（2022·河北沧州·九年级期末）在矩形ABCD中，E是CD边上的一点，是等边三角形，AC交BE于点F，则______；______．
15．（2022·河北邢台·九年级期末）如图，以正方形的对角线AC的长为边长作等边三角形AEF，，△AEF绕点A旋转，当CF最大时，则______，当CF最小时，阴影部分的面积为______．

16．（2022·河北唐山·九年级期末）如图，某渔船在海面上朝正东方向匀速航行，在A处观测到灯塔M在北偏东60°方向上，且AM=100海里．那么该船继续航行 海里可使渔船到达离灯塔距离最近的位置．


三、解答题
17．（2022·河北衡水·九年级期末）（1）；
（2）．
18．（2022·河北石家庄·九年级期末）（1）解方程：；
（2）计算：
19．（2022·河北石家庄·九年级期末）图1是一种折叠门，由上下轨道和两扇长宽相等的活页门组成，整个活页门的右轴固定在门框
上，通过推动左侧活页门开关；图2是其俯视图简化示意图，已知轨道 ,两扇活页门的宽 ,点固定，当点在上左右运动时，与的长度不变(所有结果保留小数点后一位).
    (1)若,求的长；
    (2)当点从点向右运动60时，求点在此过程中运动的路径长.
（参考数据：sin50°≈0.77,  cos50°≈0.64,  tan50°≈1.19,  π取3.14）

图1                                                           图2
20．（2022·河北唐山·九年级期末）如图，一艘渔船正以30海里/小时的速度由西向东赶鱼群，在A处看风小岛C在船的北偏东60°．40分钟后，渔船行至B处，此时看见小岛C在船的北偏东30°．已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区，问这艘渔船继续向东追赶鱼群，是否有进入危险区的可能．
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

21．（2022·河北承德·九年级期末）图1是挂墙式淋浴花洒的实物图，图2是抽象出来的几何图形．为使身高175cm的人能方便地淋浴，应当使旋转头固定在墙上的某个位置O，花洒的最高点B与人的头顶的铅垂距离为15cm，已知龙头手柄OA长为10cm，花洒直径AB是8cm，龙头手柄与墙面的较小夹角∠COA＝26°，∠OAB＝146°，则安装时，旋转头的固定点O与地面的距离应为多少？（计算结果精确到1cm，参考数据：sin26°≈0.44，cos26°≈0.90，tan26°≈0.49）

22．（2022·河北沧州·九年级期末）某体育看台侧面的示意图如图所示，观众区AC的坡度i为1：2，顶端C离水平地面AB的高度为10m，从顶棚的D处看E处的仰角α＝18°30′，竖直的立杆上C、D两点间的距离为4m，E处到观众区底端A处的水平距离AF为3m．求：
（1）观众区的水平宽度AB；
（2）顶棚的E处离地面的高度EF．（sin18°30′≈0.32，tan18°30′≈0.33，结果精确到0.1m）

23．（2022·河北石家庄·九年级期末）问题发现：
（1）如图1，内接于半径为4的，若，则_______；

问题探究：
（2）如图2，四边形内接于半径为6的，若，求四边形的面积最大值；
解决问题
（3）如图3，一块空地由三条直路（线段、AB、）和一条弧形道路围成，点是道路上的一个地铁站口，已知千米，千米，，的半径为1千米，市政府准备将这块空地规划为一个公园，主入口在点处，另外三个入口分别在点、、处，其中点在上，并在公园中修四条慢跑道，即图中的线段、、、，是否存在一种规划方案，使得四条慢跑道总长度（即四边形的周长）最大？若存在，求其最大值；若不存在，说明理由.
24．（2022·河北沧州·九年级期末）如图，某无人机爱好者在一小区外放飞无人机，当无人机飞行到一定高度D点处时，无人机测得操控者A的俯角为75°，测得小区楼房BC顶端点C处的俯角为45°．已知操控者A和小区楼房BC之间的距离为45米，小区楼房BC的高度为米．求此时无人机的高度；（假设定点A，B，C，D都在同一平面内．参考数据：，．计算结果保留根号）

25．（2022·河北保定·九年级期末）我市某乡镇学校教学楼后面靠近一座山坡，坡面上是一块平地，如图所示，BC∥AD，斜坡AB＝40米，坡角∠BAD＝60°，为防夏季因瀑雨引发山体滑坡，保障安全，学校决定对山坡进行改造，经地质人员勘测，当坡角不超过45°时，可确保山体不滑坡，改造时保持坡脚A不动，从坡顶B沿BC削进到E处，问BE至少是多少米？（结果保留根号）．

26．（2022·河北秦皇岛·九年级期末）如图，在一次数学课外实践活动中，要求测教学楼的高度AB．小刚在D处用高1.5m的测角仪CD，测得教学楼顶端A的仰角为30°，然后向教学楼前进40m到达E，又测得教学楼顶端A的仰角为60°．求这幢教学楼的高度AB．（≈1.41，≈1.73）


参考答案：
1．A
【解析】首先利用勾股定理求得AB的长，然后利用余弦的定义即可求解．
解：在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，
∴，
则cosA=．
故选：A．
本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
2．C
【解析】根据题意画出图形，由勾股定理求出AB的长，再根据三角函数的定义解答即可．
如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，

∴AB==5，
∴cos∠B=，
故选C．
本题考查锐角三角函数的定义，关键是熟练掌握在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
3．C
根据锐角三角函数的概念，可知在直角三角形中，各边的长度都扩大3倍，锐角A的三角函数值不变．
故选C．
4．B
【解析】关于x轴对称的点，横坐标相同，纵坐标互为相反数，可得答案．
解∵点（-sin60°，cos60°）即为点（-，），
∴点（-sin60°，cos60°）关于x轴对称的点的坐标是（-，-）．
故选B．
本题考查了关于x轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．
5．B
【解析】根据已知可设AC＝4a，AB＝5a，利用勾股定理求出BC，即可解答．
解：在Rt△ABC中，∠C＝90°，，
∴，
设AC＝4a，AB＝5a，
∴BC＝，
∴tanB＝，
故选：B．
本题考查了互余两角三角函数的的关系，根据已知可设AC＝4a，AB＝5a，利用勾股定理求出BC的长是解题的关键．
6．A
【解析】根据勾股定理和三角函数求解．
∵在中，，
∴
在中，，
故选：A．
本题主要考查勾股定理和三角函数．如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么．
7．D
【解析】解直角三角形，已知一条直角边和一个锐角，求斜边的长．

，
．
故选D．
本题考查解直角三角形应用，掌握特殊锐角三角函数的值是解题关键．
8．C
【解析】设PA=PB=PB′=x，在RT△PCB′中，根据，列出方程即可解决问题．
解：设PA=PB=PB′=x，
在RT△PCB′中，
∴
∴，
∴（1-）x=1，
∴x=．
故选C．
本题考查解直角三角形、三角函数等知识，解题的关键是设未知数列方程，属于中考常考题型．
9．D
【解析】先根据题意得出AD的长，在Rt△AED中利用锐角三角函数的定义求出ED的长，由CE＝CD＋DE即可得出结论．
解：∵AB⊥BC，DE⊥BC，AD∥BC，
∴四边形ABCD是矩形，
∵BC＝15m，AB＝1.5m，
∴AD＝BC＝15m，DC＝AB＝1.5m，
在Rt△AED中，
∵∠EAD＝30°，AD＝15m，
∴ED＝AD•tan30°＝15×＝5，
∴CE＝CD＋DE＝．
故选：D．
本题考查的是解直角三角形在实际生活中的应用，熟知锐角三角函数的定义是解答此题的关键，属于基本知识的考查．
10．A
∵堤坝横断面迎水坡AB的坡比是1：，
∴，
∵BC=50，
∴AC=50，
∴（m）．
故选A
11．D
【解析】根据题意确定∠CAB的度数，再利用三角函数求解即可．
解：如图，
∵点在点A的南偏西方向上，
∴∠CAB=50°．
∵该河道为东西流向且与河岸平行，点B在点A正南方向，
∴AB⊥BC．
∵点向正西方向走a米到达点，
∴BC=a．
∵，
∴．
故选：D．

本题考查的是解直角三角形的实际应用，涉及到三角函数值的问题，解决本题的关键是读懂题意，能在图形中找出相应的角或线段，牢记三角函数公式等，考查了学生应用数学的意识与能力．
12．##0.5
【解析】过点B作BD⊥AC于点D，由题可知，点D恰在格点上，令小方格的边长为1，则BD=，CD=，求得．
解：过点B作BD⊥AC于点D，
由题可知，点D恰在格点上，
∴三角形ABD和三角形BCD为直角三角形，
令小方格的边长为1，
∴BD=，CD=，
∴．
故答案为：．

本题考查了等腰直角三角形的性质，求一个角的正切值，解决问题的关键是构建直角三角形进而求解．
13．3
【解析】代入特殊角三角函数值，化简零次幂，然后再计算．
解：原式＝2×1+1
＝2+1
＝3，
故答案为：3．
本题考查实数的混合运算，理解a0＝1（a≠0），熟记特殊角三角函数值是解题关键．
14．         
【解析】先证明得到，再通过平行证明即可得到的值；
通过已知条件得到，再通过勾股定理分别求出AD、AC的长度，便可求解．

四边形ABCD是矩形，是等边三角形

，

；
故答案为：；
四边形ABCD是矩形，是等边三角形


设，则
在中，由勾股定理得
在中，由勾股定理得

故答案为：．
本题考查了矩形的性质、等边三角形的性质、全等三角形的判定及性质、相似三角形的判定及性质、勾股定理、三角函数，知识点较多，能够综合运用上述知识是解题的关键．
15．         
【解析】①当CF最大时，即CF为以A为圆心AC为半径的圆的直径，过点A作AM⊥CE，垂足为点M，根据已知条件可得到△AEC为等腰三角形，进而得到，然后根据即可求解；
②当CF最小时，即点C与点F重合时，过点A作AN⊥CE，垂足为点N，根据即可求解．
解：∵AB＝1，四边形ABCD为正方形，
∴，
①当CF最大时，即CF为以A为圆心AC为半径的圆的直径，如下图所示：

过点A作AM⊥CE，垂足为点M，
∵△AEF为等边三角形，
∴AF＝AE，∠FAE＝60°，
∴AE＝AC，∠EAC＝120°，
∴△AEC为等腰三角形，
∵AM⊥CE，
∴，
在Rt△AMC中，
，即，
∴MC=，
∴；
故答案为：；
②当CF最小时，即点C与点F重合时，如下图所示：

过点A作AN⊥CE，垂足为点N，在Rt△ANC中，
，
∴，
，
∵，
∴，
故答案为：．
本题考查正方形的性质、等腰三角形的性质、等边三角形的性质、解直角三角形，解题的关键是综合运用相关知识解题．
16．
解：如图，过M作东西方向的垂线，设垂足为N．

则∠MAN=90°-60°=30°．
在Rt△AMN中，∵∠ANM=90°，∠MAN=30°，AM=100海里，
∴AN=AM•cos∠MAN=100×=海里．
故该船继续航行海里可使渔船到达离灯塔距离最近的位置．

17．（1）；（2），．
【解析】（1）原式第一项化为最简二次根式，第二项利用特殊角的三角函数值计算，第三项利用利用零指数幂法则计算即可得到结果；
（2）先把方程化为一般式，然后利用因式分解法解方程．
解析：（1）原式==；
（2），（2y﹣1）（y+2）=0，2y﹣1=0或y+2=0，
所以，．

18．（1），；（2）2
【解析】（1）先移项，再利用提公因式法将方程的左边因式分解，继而得出两个关于x的一元一次方程，再进一步求解即可；
（2）代入三角函数值，再进一步计算即可．
（1）解：2（x﹣3）2＝x2﹣9，
2（x﹣3）2﹣（x+3）（x﹣3）＝0，
（x﹣3）（x﹣9）＝0，
则x﹣3＝0或x﹣9＝0，
解得x1＝3，x2＝9；
（2）解：
＝2×+1﹣
＝+1﹣（﹣1）
＝+1﹣+1
＝2．
本题主要考查解一元二次方程，解一元二次方程常用的方法有：直接开平方法、因式分解法、公式法及配方法，解题的关键是根据方程的特点选择简便的方法．
19．（1）43.2cm.  （2）62.8cm.
【解析】（1）如图，作OH⊥AB于H，在Rt△OBH中， 由cos∠OBC= ，求得BH的长，再根据AC=AB－2BH即可求得AC的长；
（2）由题意可知△OBC是等边三角形，由此即可求出弧OC的长，即点O在此过程中运动的路径长.
（1）如图，作OH⊥AB于H，

∵OC=OB=60，∴CH=BH，
在Rt△OBH中，
∵ cos∠OBC= ，
∴BH= OB·cos50°≈60×0.64=38.4，
∴AC=AB－2BH≈120－2×38.4=43.2，
∴AC的长约为43.2cm；
（2）∵AC=60，∴BC=60 ，
∵OC=OB=60，
∴OC=OB=BC=60 ，
∴△OBC是等边三角形，
∴的长==2 =62.8，
∴点O在此过程中运动的路径长约为62.8cm.

本题考查了解直角三角形的应用，等腰三角形的性质、等边三角形的判定与性质、弧长公式等，结合题意正确画出图形是解题的关键.
20．不可能．
【解析】根据题意实质是比较C点到AB的距离与10的大小．因此作CD⊥AB于D点，求CD的长．
解：作CD⊥AB于D，
根据题意，AB=30×=20，∠CAD=30°，∠CBD=60°，
在Rt△ACD中，AD=CD，
在Rt△BCD中，BD=CD，
∵AB=AD﹣BD，
∴CD﹣CD=20，
CD=＞10，
所以不可能．

本题考查解直角三角形的应用-方向角问题．
21．177cm
【解析】记地面水平线为，通过作辅助线构造直角三角形，分别在Rt和在Rt中，根据锐角三角函数求出OE、BF，而点B到地面的高度为175+15＝190cm，进而求OG即可．
解：如图，过点B作地面的垂线，垂足为D，
过点 A作地面GD的平行线，交OC于点E，交BD于点F，
在Rt中，∠AOE＝26°，OA＝10，
则OE＝OA•cos∠AOE≈10×0.90＝9cm，




在Rt中，∠BAF＝30°，AB＝8，
则BF＝AB•sin∠BOF＝8×＝4cm，
∴OG＝BD﹣BF﹣OE＝（175+15）﹣4﹣9＝177cm，
答：旋转头的固定点O与地面的距离应为177cm．

本题考查的是解直角三角形的实际应用，掌握构造直角三角形与矩形，利用锐角三角函数与矩形的性质是解题的关键．
22．（1）20m；（2）21.6m
【解析】（1）由AB⊥BC，AC的坡度i，由BC长度求AB长度即可；
（2）作CM⊥EF于M，DN⊥EF于N，则EF＝EN+MN+MF= EN+CD+BC，
（1）∵观众区AC的坡度i为1：2，CB= 10m，
∴AB＝2BC＝20（m），             
答：观众区的水平宽度AB为20m；
（2）如图，作CM⊥EF于M，DN⊥EF于N，

则四边形MFBC、MCDN为矩形，
∴MF＝BC＝10，MN＝CD＝4，DN＝MC＝BF＝23，
在Rt△END中，tan∠EDN＝，则EN＝DN•tan∠EDN≈7.59，
∴EF＝EN+MN+MF＝7.59+4+10≈21.6（m），
答：顶棚的E处离地面的高度EF约为21.6m．
本题考查了解直角三角形的实际应用，弄清坡度的概念，将实际问题中的数量关系归结为解直角三角形的问题，当有些图形不是直角三角形时，可适当添加辅助线，把它们分割成直角三角形或矩形是解决本题的关键．
23．（1）；（2）四边形ABCD的面积最大值是；（3）存在，其最大值为.
【解析】（1）连接OA、OB，作OH⊥AB于H，利用求出∠AOH=∠AOB=，根据OA=4，利用余弦公式求出AH，即可得到AB的长；
（2）连接AC，由得出AC=，再根据四边形的面积= ，当DH+BM最大时，四边形ABCD的面积最大，得到BD是直径，再将AC、BD的值代入求出四边形面积的最大值即可；
（3）先证明△ADM≌△BMC,得到△CDM是等边三角形，求得等边三角形的边长CD，再根据完全平方公式的关系得出PD=PC时PD+PC最大，根据CD、∠DPC求出PD，即可得到四边形周长的最大值.
（1）连接OA、OB，作OH⊥AB于H，
∵，
∴∠AOB=120.
∵OH⊥AB，
∴∠AOH=∠AOB=，AH=BH=AB，
∵OA=4，
∴AH=，
∴AB=2AH=.
故答案为：.

（2）∵∠ABC=120,四边形ABCD内接于，
∴∠ADC=60，
∵的半径为6，
∴由（1）得AC=,
如图，连接AC，作DH⊥AC,BM⊥AC,
∴四边形的面积= ,
当DH+BM最大时，四边形ABCD的面积最大，连接BD，则BD是的直径，

∴BD=2OA=12，BD⊥AC，
∴四边形的面积=.
∴四边形ABCD的面积最大值是
（3）存在；
∵千米，千米，，
∴△ADM≌△BMC,
∴DM=MC,∠AMD=∠BCM,
∵∠BCM+∠BMC=180-∠B=120，
∴∠AMD+∠BMC=120，
∴∠DMC=60，
∴△CDM是等边三角形，
∴C、D、M三点共圆，
∵点P在弧CD上,
∴C、D、M、P四点共圆，
∴∠DPC=180-∠DMC=120，
∵弧的半径为1千米，∠DMC=60，
∴CD=,
∵,
∴,
∴,
∴当PD=PC时，PD+PC最大，此时点P在弧CD的中点，交DC于H ,
在Rt△DPH中，∠DHP=90,∠DPH=60，DH=DC=,
∴，
∴四边形的周长最大值=DM+CM+DP+CP=.
此题是一道综合题，考查圆的性质，垂径定理，三角函数，三角形全等的判定及性质，动点最大值等知识点.（1）中问题发现的结论应用很主要，理解题意在（2）、（3）中应用解题，（3）的PD+PC最大值的确定是难点，注意与所学知识的结合才能更好的解题.
24．米
【解析】先添加辅助线，如详解中的图，然后设EC为x，利用正位置和两边关系建立方程，解出x即可．
解：如图1，过D点作，垂足为点H，过C点作，垂足为点E，

可知四边形EHBC为矩形，
∴，，
∵无人机测得小区楼房BC顶端点C处的俯角为45°，测得操控者A的俯角为75°，，
∴，，
∴，
∴，
设，
∴，，
在中，，
即，
解得：，
∴
∴此时无人机的高度为米．
本题考查三角函数在解直角三角形中的应用，正确建立方程等式是关键．
25．BE至少是20（﹣1）米．
【解析】根据三角函数值先求得斜坡的高度，再得到AF、AG的值，进而求解．
作BG⊥AD于G，作EF⊥AD于F，则在Rt△ABG中，∠BAD＝60°，AB＝40，
所以就有，AG＝AB•Cos60°＝20，
同理在Rt△AEF中，∠EAD＝45°，
则有AF＝EF＝BG＝20，
所以米．
故BE至少是米．
本题考查锐角三角函数的应用．需注意构造直角三角形是常用的辅助线方法．
26．这幢教学楼的高度AB是36.1m
【解析】利用60°的正弦值可求AG长，加上1.5m即为这幢教学楼的高度AB．
解：∵∠ACG=30°，∠AFG=60°
∴∠FAC=30°
∴∠ACG=∠FAC
∴AF=CF=40m
在Rt△AFG中，∵sin∠AFG=
∴AG=AF×sin∠AFG=40×sin60°
=40× ≈20×1.73=34.6(m)
∴AB=34.6+1.5=36.1 (m)
答：这幢教学楼的高度AB是36.1m.
构造仰角所在的直角三角形，利用两个直角三角形的公共边求解是常用的解直角三角形的方法