



2020-2022年湖南中考数学3年真题汇编 专题26 动点综合问题(学生卷+教师卷)
展开专题26 动点综合问题
一、单选题
1.(2022·广西河池)东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )
A. B.C. D.
2.(2022·甘肃武威)如图1,在菱形中,,动点从点出发,沿折线方向匀速运动,运动到点停止.设点的运动路程为,的面积为,与的函数图象如图2所示,则的长为( )
A. B. C. D.
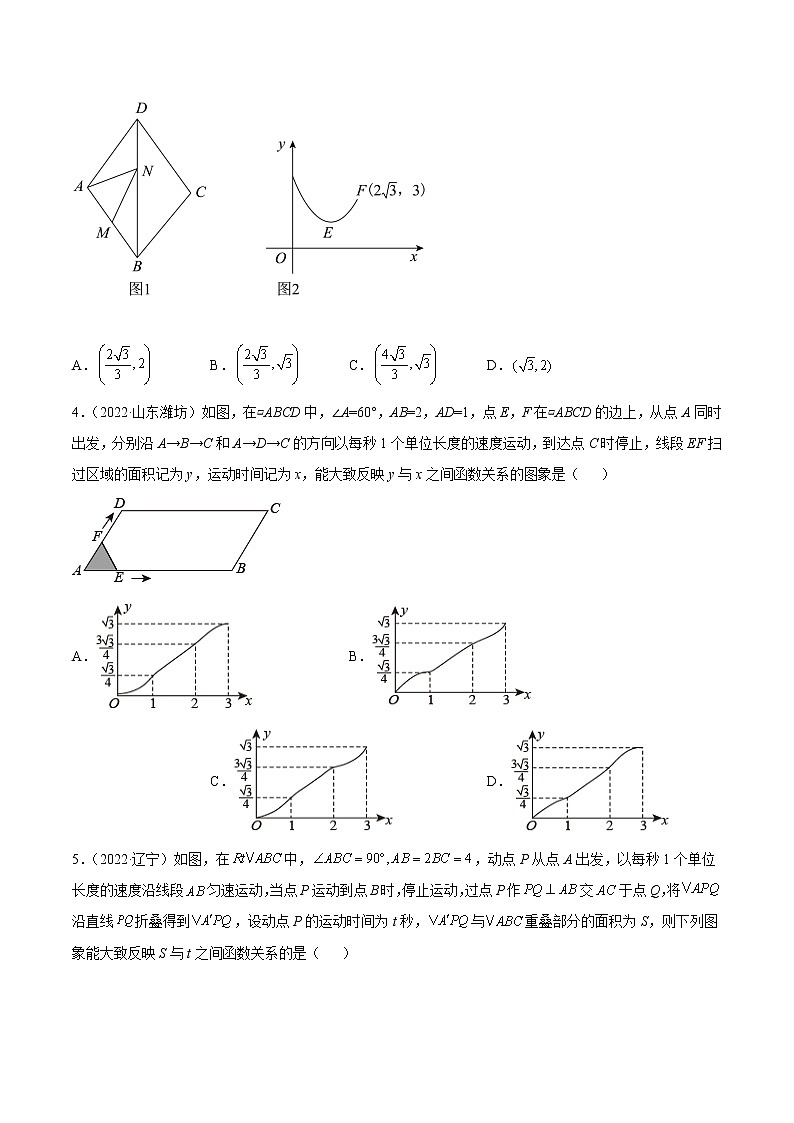
3.(2022·四川绵阳)如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F的坐标为,则图象最低点E的坐标为( )
A. B. C. D.
4.(2022·山东潍坊)如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A. B. C. D.
5.(2022·辽宁)如图,在中,,动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到,设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B. C. D.
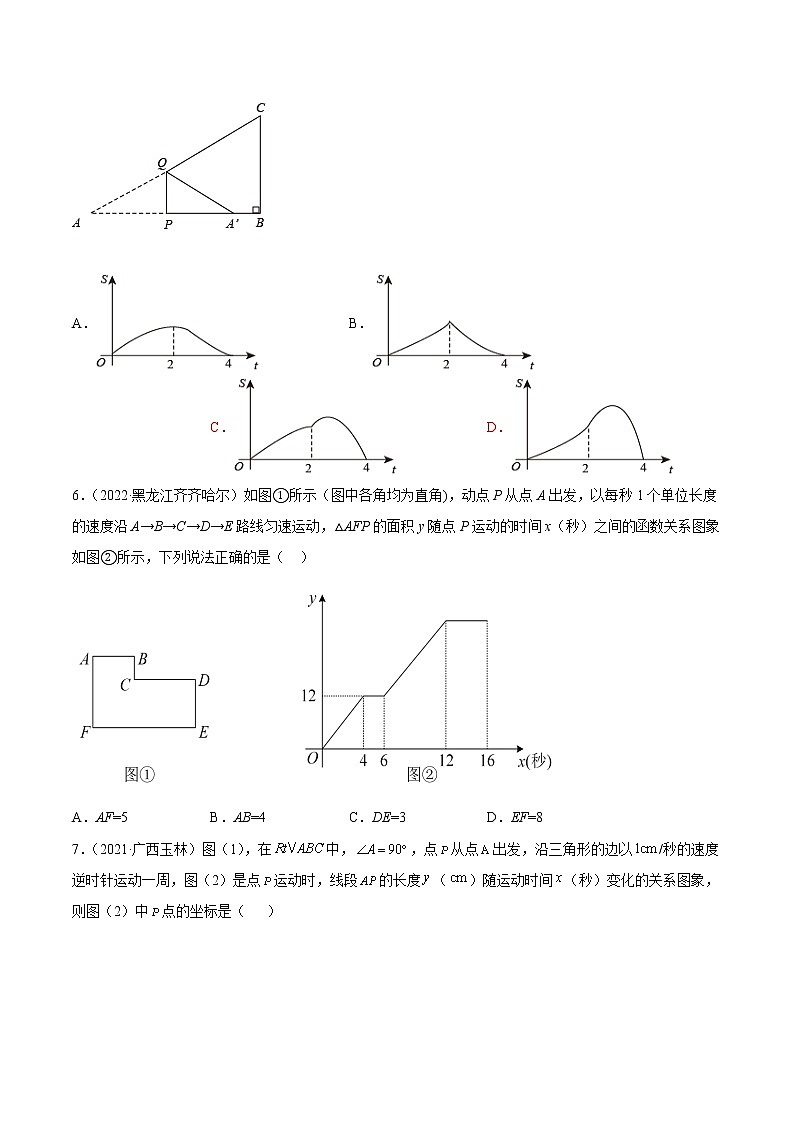
6.(2022·黑龙江齐齐哈尔)如图①所示(图中各角均为直角),动点Р从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y随点Р运动的时间x(秒)之间的函数关系图象如图②所示,下列说法正确的是( )
A.AF=5 B.AB=4 C.DE=3 D.EF=8
7.(2021·广西玉林)图(1),在中,,点从点出发,沿三角形的边以/秒的速度逆时针运动一周,图(2)是点运动时,线段的长度()随运动时间(秒)变化的关系图象,则图(2)中点的坐标是( )
A. B. C. D.
8.(2020·湖北荆门)在平面直角坐标系中,长为2的线段(点D在点C右侧)在x轴上移动,,连接、,则的最小值为( )
A. B. C. D.
9.(2020·四川乐山)数轴上点表示的数是,将点在数轴上平移个单位长度得到点.则点表示的数是( )
A. B.或
C. D.或
10.(2021·山东泰安)如图,在矩形中,,,点P在线段上运动(含B、C两点),连接,以点A为中心,将线段逆时针旋转60°到,连接,则线段的最小值为( )
A. B. C. D.3
11.(2021·辽宁阜新)如图,弧长为半圆的弓形在坐标系中,圆心在.将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为时,圆心的横坐标是( )
A. B. C. D.
12.(2021·广东)设O为坐标原点,点A、B为抛物线上的两个动点,且.连接点A、B,过O作于点C,则点C到y轴距离的最大值( )
A. B. C. D.1
二、填空题
13.(2021·湖南衡阳)如图1,菱形的对角线与相交于点O,P、Q两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为,点Q的运动路线为.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为__________厘米.
14.(2021·四川眉山)如图,在菱形中,,对角线、相交于点,点在线段上,且,点为线段上的一个动点,则的最小值是______.
15.(2020·内蒙古赤峰)一个电子跳蚤在数轴上做跳跃运动.第一次从原点O起跳,落点为A1,点A1表示的数为1;第二次从点A1起跳,落点为OA1的中点A2;第三次从A2点起跳,落点为0A2的中点A3;如此跳跃下去……最后落点为OA2019的中点A2020.则点A2020表示的数为__________.
16.(2022·湖北黄冈)如图1,在△ABC中,∠B=36°,动点P从点A出发,沿折线A→B→C匀速运动至点C停止.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示.当AP恰好平分∠BAC时,t的值为________.
17.(2021·江苏淮安)如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是___.
18.(2020·内蒙古通辽)如图①,在中,,点E是边的中点,点P是边上一动点,设.图②是y关于x的函数图象,其中H是图象上的最低点..那么的值为_______.
19.(2019·四川乐山)如图1,在四边形中,∥,,直线.当直线沿射线方向,从点开始向右平移时,直线与四边形的边分别相交于点、.设直线向右平移的距离为,线段的长为,且与的函数关系如图2所示,则四边形的周长是_____.
20.(2022·广西柳州)如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为 _____.
21.(2020·山东滨州)如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为则正方形ABCD的面积为________
三、解答题
22.(2020·河北)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率;
(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对次,且他最终停留的位置对应的数为,试用含的代数式表示,并求该位置距离原点最近时的值;
(3)从图的位置开始,若进行了次移动游戏后,甲与乙的位置相距2个单位,直接写出的值.
23.(2021·甘肃兰州)在中,,,,将绕点顺时针旋转,角的两边分别交射线于,两点,为上一点,连接,且(当点,重合时,点,也重合).设,两点间的距离为,,两点间的距离为.
小刚根据学习函数的经验,对因变量随着自变量的变化而变化的规律进行了探究.
下面是小刚的探究过程,请补充完整.
(1)列表:下表的已知数据是根据,两点间的距离进行取点,画图,测量分别得到了与的几组对应值;
0
1
2
3
4
5
6
7
8
请你通过计算补全表格:______;
(2)描点、连线:在平面直角坐标系中,描出表中各组数值所对应的点,并画出函数关于的图像;
(3)探究性质:随着自变量的不断增大,函数的变化趋势;
(4)解决问题:当时,的长度大约是______.(结果保留两位小数)
24.(2020·吉林长春)如图①,在中,,,.点从点出发,沿折线以每秒5个单位长度的速度向点运动,同时点从点出发,沿以每秒2个单位长度的速度向点运动,点到达点时,点、同时停止运动.当点不与点、重合时,作点关于直线的对称点,连结交于点,连结、.设点的运动时间为秒.
(1)当点与点重合时,求的值.
(2)用含的代数式表示线段的长.
(3)当为锐角三角形时,求的取值范围.
(4)如图②,取的中点,连结.当直线与的一条直角边平行时,直接写出的值.
25.(2020·湖南益阳)定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形,根据以上定义,解决下列问题:
(1)如图1,正方形中,是上的点,将绕点旋转,使与重合,此时点的对应点在的延长线上,则四边形为“直等补”四边形,为什么?
(2)如图2,已知四边形是“直等补”四边形,,,,点到直线的距离为.
①求的长.
②若、分别是、边上的动点,求周长的最小值.
26.(2022·天津)将一个矩形纸片放置在平面直角坐标系中,点,点,点,点P在边上(点P不与点O,C重合),折叠该纸片,使折痕所在的直线经过点P,并与x轴的正半轴相交于点Q,且,点O的对应点落在第一象限.设.
(1)如图①,当时,求的大小和点的坐标;
(2)如图②,若折叠后重合部分为四边形,分别与边相交于点E,F,试用含有t的式子表示的长,并直接写出t的取值范围;
(3)若折叠后重合部分的面积为,则t的值可以是___________(请直接写出两个不同的值即可).
27.(2021·辽宁大连)如图,四边形为矩形,,,P、Q均从点B出发,点P以2个单位每秒的速度沿的方向运动,点Q以1个单位每秒的速度沿运动,设运动时间为t秒.
(1)求的长;
(2)若,求S关于t的解析式.
28.(2021·广西来宾)如图①,在中,于点,,,点是上一动点(不与点,重合),在内作矩形,点在上,点,在上,设,连接.
(1)当矩形是正方形时,直接写出的长;
(2)设的面积为,矩形的面积为,令,求关于的函数解析式(不要求写出自变量的取值范围);
(3)如图②,点是(2)中得到的函数图象上的任意一点,过点的直线分别与轴正半轴,轴正半轴交于,两点,求面积的最小值,并说明理由.
29.(2021·海南)已知抛物线与x轴交于两点,与y轴交于C点,且点A的坐标为、点C的坐标为.
(1)求该抛物线的函数表达式;
(2)如图1,若该抛物线的顶点为P,求的面积;
(3)如图2,有两动点在的边上运动,速度均为每秒1个单位长度,它们分别从点C和点B同时出发,点D沿折线按方向向终点B运动,点E沿线段按方向向终点C运动,当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,请解答下列问题:
①当t为何值时,的面积等于;
②在点运动过程中,该抛物线上存在点F,使得依次连接得到的四边形是平行四边形,请直接写出所有符合条件的点F的坐标.
30.(2020·辽宁营口)如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1,若k=1,则AF与AE之间的数量关系是 ;
(2)如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.
31.(2020·湖南怀化)如图所示,抛物线与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
(1)求点C及顶点M的坐标.
(2)若点N是第四象限内抛物线上的一个动点,连接求面积的最大值及此时点N的坐标.
(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与相似.若存在,求出点P的坐标;若不存在,请说明理由.
32.(2020·江苏连云港)(1)如图1,点为矩形对角线上一点,过点作,分别交、于点、.若,,的面积为,的面积为,则________;
(2)如图2,点为内一点(点不在上),点、、、分别为各边的中点.设四边形的面积为,四边形的面积为(其中),求的面积(用含、的代数式表示);
(3)如图3,点为内一点(点不在上)过点作,,与各边分别相交于点、、、.设四边形的面积为,四边形的面积为(其中),求的面积(用含、的代数式表示);
(4)如图4,点、、、把四等分.请你在圆内选一点(点不在、上),设、、围成的封闭图形的面积为,、、围成的封闭图形的面积为,的面积为,的面积为.根据你选的点的位置,直接写出一个含有、、、的等式(写出一种情况即可).
33.(2020·四川遂宁)如图,抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),C(0,6)三点.
(1)求抛物线的解析式.
(2)抛物线的顶点M与对称轴l上的点N关于x轴对称,直线AN交抛物线于点D,直线BE交AD于点E,若直线BE将△ABD的面积分为1:2两部分,求点E的坐标.
(3)P为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点P,使A、D、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
34.(2022·辽宁大连)如图,在中,,,点D在上,,连接,,点P是边上一动点(点P不与点A,D,C重合),过点P作的垂线,与相交于点Q,连接,设,与重叠部分的面积为S.
(1)求的长;
(2)求S关于x的函数解析式,并直接写出自变量x的取值范围.
35.(2022·山东青岛)如图,在中,,将绕点A按逆时针方向旋转得到,连接.点P从点B出发,沿方向匀速运动,速度为;同时,点Q从点A出发,沿方向匀速运动,速度为.交于点F,连接.设运动时间为.解答下列问题:
(1)当时,求t的值;
(2)设四边形的面积为,求S与t之间的函数关系式;
(3)是否存在某一时刻t,使?若存在,求出t的值;若不存在,请说明理由.
36.(2021·湖南张家界)如图,已知二次函数的图象经过点且与轴交于原点及点.
(1)求二次函数的表达式;
(2)求顶点的坐标及直线的表达式;
(3)判断的形状,试说明理由;
(4)若点为上的动点,且的半径为,一动点从点出发,以每秒2个单位长度的速度沿线段匀速运动到点,再以每秒1个单位长度的速度沿线段匀速运动到点后停止运动,求点的运动时间的最小值.
37.(2021·江苏无锡)在平面直角坐标系中,O为坐标原点,直线与x轴交于点B,与y轴交于点C,二次函数的图象过B、C两点,且与x轴交于另一点A,点M为线段上的一个动点,过点M作直线l平行于y轴交于点F,交二次函数的图象于点E.
(1)求二次函数的表达式;
(2)当以C、E、F为顶点的三角形与相似时,求线段的长度;
(3)已知点N是y轴上的点,若点N、F关于直线对称,求点N的坐标.
38.(2021·吉林长春)如图,在中,,,,点D为边AC的中点.动点P从点A出发,沿折线AB—BC以每秒1个单位长度的速度向点C运动,当点P不与点A、C重合时,连结PD.作点A关于直线PD的对称点,连结、.设点P的运动时间为t秒.
(1)线段AD的长为 .
(2)用含t的代数式表示线段BP的长.
(3)当点在内部时,求的取值范围.
(4)当与相等时,直接写出的值.
39.(2021·湖南怀化)如图所示,抛物线与x轴交于A、B两点,与y轴交于点C,且,,,抛物线的对称轴与直线BC交于点M,与x轴交于点N.
(1)求抛物线的解析式;
(2)若点P是对称轴上的一个动点,是否存在以P、C、M为顶点的三角形与相似?若存在,求出点P的坐标,若不存在,请说明理由.
(3)D为CO的中点,一个动点G从D点出发,先到达x轴上的点E,再走到抛物线对称轴上的点F,最后返回到点C.要使动点G走过的路程最短,请找出点E、F的位置,写出坐标,并求出最短路程.
(4)点Q是抛物线上位于x轴上方的一点,点R在x轴上,是否存在以点Q为直角顶点的等腰?若存在,求出点Q的坐标,若不存在,请说明理由.
40.(2021·浙江丽水)如图,在菱形中,是锐角,E是边上的动点,将射线绕点A按逆时针方向旋转,交直线于点F.
(1)当时,
①求证:;
②连结,若,求的值;
(2)当时,延长交射线于点M,延长交射线于点N,连结,若,则当为何值时,是等腰三角形.
41.(2018·山东青岛)已知:如图,四边形ABCD,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,以QA、QP为边作平行四边形AQPE,设运动的时间为t(s),0<t<5.
根据题意解答下列问题:
(1)用含t的代数式表示AP;
(2)设四边形CPQB的面积为S(cm2),求S与t的函数关系式;
(3)当QP⊥BD时,求t的值;
(4)在运动过程中,是否存在某一时刻t,使点E在∠ABD的平分线上?若存在,求出t的值;若不存在,请说明理由.
42.(2013·贵州遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
43.(2020·辽宁辽宁)如图,抛物线与轴相交于点和点,与轴相交于点,作直线.
(1)求抛物线的解析式;
(2)在直线上方的抛物线上存在点,使,求点的坐标;
(3)在(2)的条件下,点的坐标为,点在抛物线上,点在直线上,当以为顶点的四边形是平行四边形时,请直接写出点的坐标.
44.(2020·辽宁大连)如图,中,,点D从点B出发,沿边以的速度向终点C运动,过点D作,交边(或)于点E.设点D的运动时间为,的面积为.
(1)当点D与点A重合时,求t的值;
(2)求S关于t的函数解析式,并直接写出自变量t的取值范围.
45.(2020·内蒙古呼伦贝尔)如图,抛物线与轴交于点和点,与轴交于点,连接,点是线段上的动点(与点不重合),连接并延长交抛物线于点,连接,设点的横坐标为.
(1)求抛物线的解析式和点的坐标;
(2)当的面积等于2时,求的值;
(3)在点运动过程中,是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
46.(2020·湖北随州)如图,在平面直角坐标系中,抛物线的对称轴为直线,其图象与轴交于点和点,与轴交于点.
(1)直接写出抛物线的解析式和的度数;
(2)动点,同时从点出发,点以每秒3个单位的速度在线段上运动,点以每秒个单位的速度在线段上运动,当其中一个点到达终点时,另一个点也随之停止运动.设运动的时间为秒,连接,再将线段绕点顺时针旋转,设点落在点的位置,若点恰好落在抛物线上,求的值及此时点的坐标;
(3)在(2)的条件下,设为抛物线上一动点,为轴上一动点,当以点,,为顶点的三角形与相似时,请直接写出点及其对应的点的坐标.(每写出一组正确的结果得1分,至多得4分)
47.(2020·河北)如图1和图2,在中,,,.点在边上,点,分别在,上,且.点从点出发沿折线匀速移动,到达点时停止;而点在边上随移动,且始终保持.
(1)当点在上时,求点与点的最短距离;
(2)若点在上,且将的面积分成上下4:5两部分时,求的长;
(3)设点移动的路程为,当及时,分别求点到直线的距离(用含的式子表示);
(4)在点处设计并安装一扫描器,按定角扫描区域(含边界),扫描器随点从到再到共用时36秒.若,请直接写出点被扫描到的总时长.
48.(2020·山东潍坊)如图,抛物线与x轴交于点和点,与y轴交于点C,顶点为D,连接与抛物线的对称轴l交于点E.
(1)求抛物线的表达式;
(2)点P是第一象限内抛物线上的动点,连接,当时,求点P的坐标;
(3)点N是对称轴l右侧抛物线上的动点,在射线上是否存在点M,使得以点M,N,E为顶点的三角形与相似?若存在,求点M的坐标;若不存在,请说明理由.
49.(2022·湖北十堰)已知,在内部作等腰,,.点为射线上任意一点(与点不重合),连接,将线段绕点逆时针旋转得到线段,连接并延长交射线于点.
(1)如图1,当时,线段与的数量关系是_________;
(2)如图2,当时,(1)中的结论是否还成立?若成立,请给予证明;若不成立,请说明理由;
(3)若,,,过点作,垂足为,请直接写出的长(用含有的式子表示).
50.(2021·四川成都)在中,,将绕点B顺时针旋转得到,其中点A,C的对应点分别为点,.
(1)如图1,当点落在的延长线上时,求的长;
(2)如图2,当点落在的延长线上时,连接,交于点M,求的长;
(3)如图3,连接,直线交于点D,点E为的中点,连接.在旋转过程中,是否存在最小值?若存在,求出的最小值;若不存在,请说明理由.
51.(2021·内蒙古鄂尔多斯)旋转是一种重要的图形变换,当图形中有一组邻边相等时往往可以通过旋转解决问题.
(1)尝试解决:如图①,在等腰中,,点M是上的一点,,,将绕点A旋转后得到,连接,则___________.
(2)类比探究:如图②,在“筝形”四边形中,于点B,于点D,点P、Q分别是上的点,且,求的周长.(结果用a表示)
(3)拓展应用:如图③,已知四边形,,求四边形的面积.
52.(2021·黑龙江齐齐哈尔)综合与实践
数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思推空间,丰富数学体验.让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF,连接EF,如图1.
(1)_________,写出图中两个等腰三角形:_________(不需要添加字母);
转一转:将图1中的绕点A旋转,使它的两边分别交边BC、CD于点P、Q,连接PQ,如图2.
(2)线段BP、PQ、DQ之间的数量关系为_________;
(3)连接正方形对角线BD,若图2中的的边AP、AQ分别交对角线BD于点M、点N.如图3,则________;
剪一剪:将图3中的正方形纸片沿对角线BD剪开,如图4.
(4)求证:.
53.(2021·湖北宜昌)如图,在矩形中,是边上一点,,,垂足为.将四边形绕点顺时针旋转,得到四边形.所在的直线分别交直线于点,交直线于点,交于点.所在的直线分别交直线于点,交直线于点,连接交于点.
(1)如图1,求证:四边形是正方形;
(2)如图2,当点和点重合时.
①求证:;
②若,,求线段的长;
(3)如图3,若交于点,,求的值.
54.(2021·辽宁本溪)在▱中,,平分,交对角线于点G,交射线于点E,将线段绕点E顺时针旋转得线段.
(1)如图1,当时,连接,请直接写出线段和线段的数量关系;
(2)如图2,当时,过点B作于点,连接,请写出线段,,之间的数量关系,并说明理由;
(3)当时,连接,若,请直接写出与面积的比值.
55.(2022·广西)已知,点A,B分别在射线上运动,.
(1)如图①,若,取AB中点D,点A,B运动时,点D也随之运动,点A,B,D的对应点分别为,连接.判断OD与有什么数量关系?证明你的结论:
(2)如图②,若,以AB为斜边在其右侧作等腰直角三角形ABC,求点O与点C的最大距离:
(3)如图③,若,当点A,B运动到什么位置时,的面积最大?请说明理由,并求出面积的最大值.
56.(2022·辽宁沈阳)(1)如图,和是等腰直角三角形,,点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为______;
(2)如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.
(3)如图,若,点C是线段AB外一动点,,连接BC,
①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值______;
②若以BC为斜边作,(B、C、D三点按顺时针排列),,连接AD,当时,直接写出AD的值.
57.(2022·四川雅安)已知二次函数y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),且与y轴交于点C(0,﹣3).
(1)求此二次函数的表达式及图象顶点D的坐标;
(2)在此抛物线的对称轴上是否存在点E,使△ACE为Rt△,若存在,试求点E的坐标,若不存在,请说明理由;
(3)在平面直角坐标系中,存在点P,满足PA⊥PD,求线段PB的最小值.
58.(2022·湖北鄂州)如图1,在平面直角坐标系中,Rt△OAB的直角边OA在y轴的正半轴上,且OA=6,斜边OB=10,点P为线段AB上一动点.
(1)请直接写出点B的坐标;
(2)若动点P满足∠POB=45°,求此时点P的坐标;
(3)如图2,若点E为线段OB的中点,连接PE,以PE为折痕,在平面内将△APE折叠,点A的对应点为A',当PA'⊥OB时,求此时点P的坐标;
(4)如图3,若F为线段AO上一点,且AF=2,连接FP,将线段FP绕点F顺时针方向旋转60°得线段FG,连接OG,当OG取最小值时,请直接写出OG的最小值和此时线段FP扫过的面积.
59.(2022·江苏连云港)【问题情境】在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中,,.
【问题探究】小昕同学将三角板绕点B按顺时针方向旋转.
(1)如图2,当点落在边上时,延长交于点,求的长.
(2)若点、、在同一条直线上,求点到直线的距离.
(3)连接,取的中点,三角板由初始位置(图1),旋转到点、、首次在同一条直线上(如图3),求点所经过的路径长.
(4)如图4,为的中点,则在旋转过程中,点到直线的距离的最大值是_____.
60.(2021·四川宜宾)如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.
(1)求抛物线的表达式;
(2)判断△BCE的形状,并说明理由;
(3)如图2,以C为圆心,为半径作⊙C,在⊙C上是否存在点P,使得BP+EP的值最小,若存在,请求出最小值;若不存在,请说明理由.
专题34 动点综合问题(33题)(教师卷+学生卷)- 2024年中考数学真题分类汇编(全国通用): 这是一份专题34 动点综合问题(33题)(教师卷+学生卷)- 2024年中考数学真题分类汇编(全国通用),文件包含专题34动点综合问题33题教师卷-2024年中考数学真题分类汇编全国通用docx、专题34动点综合问题33题学生卷-2024年中考数学真题分类汇编全国通用docx等2份试卷配套教学资源,其中试卷共96页, 欢迎下载使用。
(2020-2022)中考数学真题分类汇编专题26 动点综合问题(教师版): 这是一份(2020-2022)中考数学真题分类汇编专题26 动点综合问题(教师版),共157页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学中考复习 专题26 动点综合问题-三年(2020-2022)中考数学真题分项汇编(全国通用)(原卷版): 这是一份初中数学中考复习 专题26 动点综合问题-三年(2020-2022)中考数学真题分项汇编(全国通用)(原卷版),共36页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












