2022-2023学年广东省深圳市翠园教育集团九年级（上）期中数学试卷（含解析）

这是一份2022-2023学年广东省深圳市翠园教育集团九年级（上）期中数学试卷（含解析），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
下列方程中①3x2+x=20；②2x2-3x+4=0；③x2-1x=4；④x2=1；⑤x2-3x+3=0，一元二次方程有( )
A. 2个B. 3个C. 4个D. 5个
已知，ab=cd=34且b+d≠0，下列各式正确的是( )
A. 3c=4dB. a+cb+d=34C. dc+d=37D. a-bb=14
下列说法：
(1)对角线互相垂直的四边形是菱形；
(2)有一个内角为直角的平行四边形是矩形；
(3)对角线互相垂直平分的四边形是正方形；
(4)两组对角相等的四边形是平行四边形；
(5)四边形各边中点连线所得的图形是平行四边形；
其中正确的有个．( )
A. 2B. 3C. 4D. 5
按照党中央、国务院决策部署，为了活跃市场主体、助推各地区经济发展，各省市地区抓紧推动稳经济一揽子政策落实落地．江夏区制定了“黄金十条”，坚定企业疫后发展信心，促进企业稳步高效增长.2022年我区某企业4月份的利润是100万元，第二季度的总利润达到500万元，设利润平均月增长率为x，则依题意列方程( )
A. 100(1+x)2=500
B. 100(1+x2)=500
C. 100(1+x)+100(1+x)2=500
D. 100+100(1+x)+100(1+x)2=500
某校举行演讲比赛，小李、小吴与另外两位同学闯入决赛，则小李和小吴获得前两名的概率是( )
A. 12B. 13C. 14D. 16
若两个数的和为6，积为5，则以这两个数为根的一元二次方程是( )
A. x2-5x+6=0B. x2-5x-6=0C. x2-6x+5=0D. x2-6x-5=0
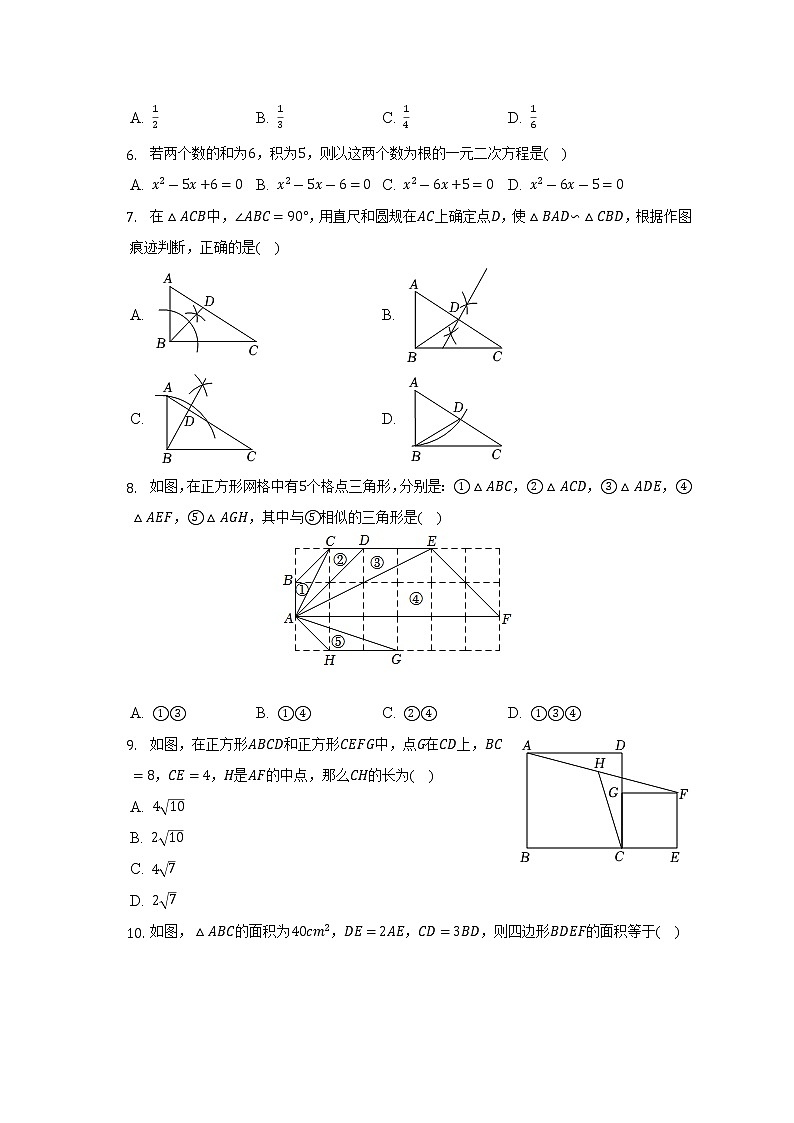
在△ACB中，∠ABC=90°，用直尺和圆规在AC上确定点D，使△BAD∽△CBD，根据作图痕迹判断，正确的是( )
A. B.
C. D.
如图，在正方形网格中有5个格点三角形，分别是：①△ABC，②△ACD，③△ADE，④△AEF，⑤△AGH，其中与⑤相似的三角形是( )
A. ①③B. ①④C. ②④D. ①③④
如图，在正方形ABCD和正方形CEFG中，点G在CD上，BC=8，CE=4，H是AF的中点，那么CH的长为( )
A. 410
B. 210
C. 47
D. 27
如图，△ABC的面积为40cm2，DE=2AE，CD=3BD，则四边形BDEF的面积等于( )
A. 10011cm2B. 9cm2C. 10511cm2D. 8.5cm2
二、填空题（本大题共5小题，共15.0分）
如果2x=3y，那么y+2xx-y=______．
如图，在线段AB上找到一个点C，且AC已知关于x的方程 (m-1)x m2+1+2x-3=0是一元二次方程，则m的值为 ．
等腰三角形的两边a、b满足a2+b2-10b=6a-34，则这个三角形的周长为______．
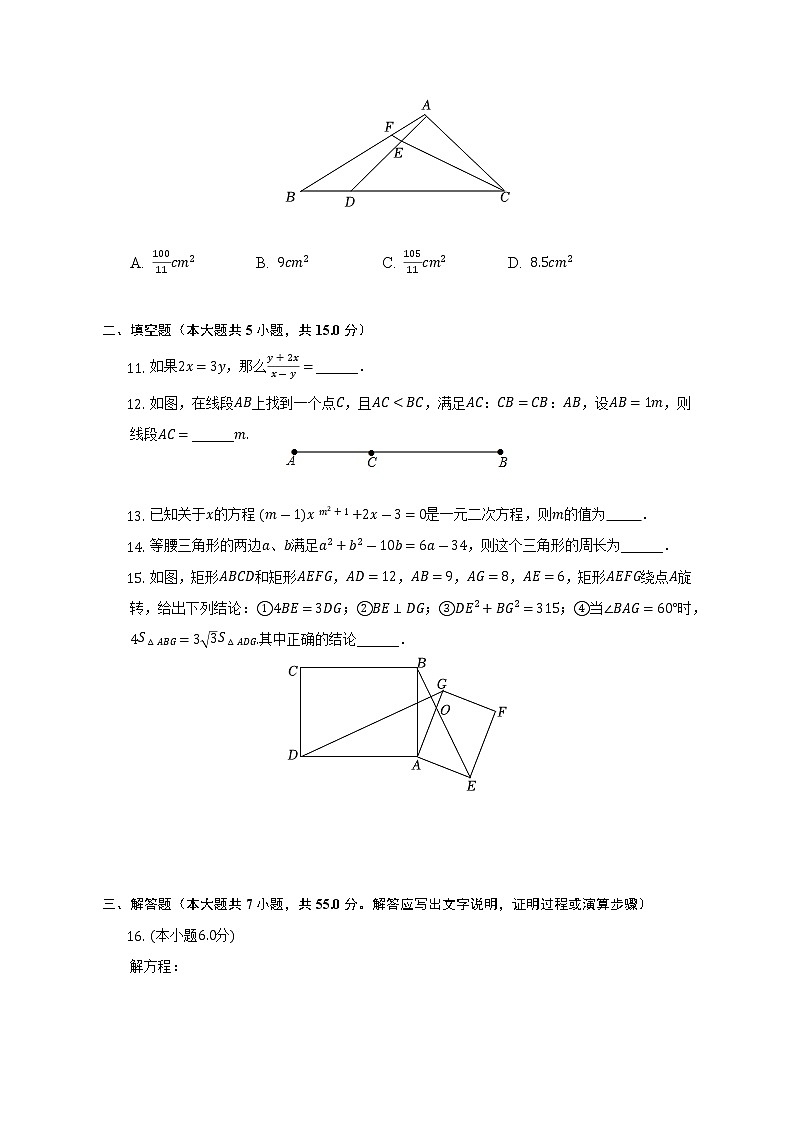
如图，矩形ABCD和矩形AEFG，AD=12，AB=9，AG=8，AE=6，矩形AEFG绕点A旋转，给出下列结论：①4BE=3DG；②BE⊥DG；③DE2+BG2=315；④当∠BAG=60°时，4S△ABG=33S△ADG.其中正确的结论______．
三、解答题（本大题共7小题，共55.0分。解答应写出文字说明，证明过程或演算步骤）
(本小题6.0分)
解方程：
(1)x2+4x-1=0；
(2)3x(x-1)=(1-x)2．
(本小题7.0分)
“双减”意见下，我区教体局对课后作业作了更明确的要求，为了解某学校七年级学生课后作业时长情况，某部门针对某校七年级学生进行了问卷调查，调查结果分四类显示：A表示“40分钟以内完成”，B表示“40-70分钟以内完成”，C表示“70-90分钟以内完成”，D表示“90分钟以上完成”.根据调查结果，绘制成两种不完整的统计图．请结合统计图，回答下列问题．
(1)这次调查的总人数是______人；扇形统计图中，B类扇形的圆心角是______°；C类扇形所占的百分比是______．
(2)在D类学生中，有2名男生和2名女生，再需从这4名学生中抽取2名学生作进一步访谈调查，请用树状图或列表的方法，求所抽2名学生恰好是1名男生和1名女生的概率．
(本小题7.0分)
已知△ABC在平面直角坐标系中的位置如图所示．
(1)在图中画出△ABC沿x轴翻折后的△A1B1C1；
(2)以点M(1,2)为位似中心，作出△A1B1C1按2：1放大后的位似图形△A2B2C2；
(3)填空：点A2的坐标______；△ABC与△A2B2C2的周长比是______．
(本小题8.0分)
如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．
(1)求证：四边形BMDN是菱形；
(2)若AB=4，AD=8，求△BMD的面积．
(本小题7.0分)
为促进新旧功能转换，提高经济效益，甘井科技公司近期研发出一种新型高科技设备，每台设备成本价为25万元，经过市场调研发现，该设备的月销售量y(台)和销售单价x(万元/台)满足如图所示的一次函数关系．
(1)求月销售量y与销售单价x之间的函数关系式(不用体现x的取值范围)；
(2)根据相关规定，此设备的销售单价不得高于28万元/台，如果该公司想获得70万元的月利润，那么该设备的销售单价应是多少？
(本小题10.0分)
在△ABC中，∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．
(1)如果AB=AC.如图①，且点D在线段BC上运动．试判断线段CF与BD之间的位置关系，并证明你的结论．
(2)如果AB≠AC，如图②，且点D在线段BC上运动．(1)中结论是否成立，为什么？
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P，设AC=42，BC=3，CD=x，求线段CP的长．(用含x的式子表示)
(本小题10.0分)
问题背景如图(1)，已知△ABC∽△ADE，求证：△ABD∽△ACE；
尝试应用如图(2)，在△ABC和△ADE中，∠BAC=∠DAE=90°，∠ABC=∠ADE=30°，AC与DE相交于点F，点D在BC边上，ADBD=3，求DFCF的值；
拓展创新如图(3)，D是△ABC内一点，∠BAD=∠CBD=30°，∠BDC=90°，AB=4，AC=23，直接写出AD的长．
答案和解析
1.【答案】C
【解析】解：一元二次方程有①3x2+x=20，②2x2-3x+4=0，④x2=1，⑤x2-3x+3=0，共4个，
故选：C．
根据一元二次方程的定义逐个判断即可．
本题考查了一元二次方程的定义，能熟记一元二次方程的定义是解此题的关键，注意：只含有一个未知数，并且所含未知数的项的最高次数是2的整式方程，叫一元二次方程．
2.【答案】B
【解析】解：∵cd=34，
∴4c=3d，所以A选项不符合题意；
∵ab=cd=34，且b+d≠0，
∴a+cb+d=34，所以B选项符合题意；
∵cd=34，
∴dc=43，
∴dc+d=43+4=47，所以C选项不符合题意；
∵ab=34，
∴a-bb=3-44=-14，所以D选项不符合题意．
故选：B．
利用比例的性质对各选项进行判断．
本题考查了比例线段：熟练掌握比例的性质(内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质)是解决问题的关键．
3.【答案】B
【解析】解：(1)对角线互相垂直的平行四边形是菱形，故错误，不符合题意；
(2)有一个内角为直角的平行四边形是矩形，正确，符合题意；
(3)对角线互相垂直平分的四边形是菱形，故原命题错误，不符合题意；
(4)两组对角相等的四边形是平行四边形，正确，符合题意；
(5)四边形各边中点连线所得的图形是平行四边形，正确，符合题意，
正确的有3个，
故选：B．
利用菱形、矩形、正方形及平行四边形的判定方法分别判断后即可确定正确的选项．
本题考查了中点四边形及特殊的平行四边形的判定方法，解题的关键是了解有关的判定方法，难度不大．
4.【答案】D
【解析】解：∵该企业4月份的利润是100万元，且利润平均月增长率为x，
∴该企业5月份的利润是100(1+x)万元，6月份的利润是100(1+x)2万元．
依题意得：100+100(1+x)+100(1+x)2=500．
故选：D．
根据该企业4月份的利润及利润平均月增长率，可得出该企业5月份的利润是100(1+x)万元，6月份的利润是100(1+x)2万元，结合该企业第二季度的总利润达到500万元，即可得出关于x的一元二次方程，此题得解．
本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
5.【答案】D
【解析】解：将另外两名同学分别记为甲、乙，
画树状图如下：

共有12种等可能的结果，其中小李和小吴获得前两名的结果有2种，
∴小李和小吴获得前两名的概率为212=16．
故选：D．
画树状图得出所有等可能的结果数，以及小李和小吴获得前两名的结果数，再利用概率公式可得出答案．
本题考查列表法与树状图法，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．
6.【答案】C
【解析】解：若两个数的和为6，积为5，则以这两个数为根的一元二次方程是x2-6x+5=0，
故选：C．
以x1，x2为根的一元二次方程是x2-(x1+x2)x+x1x2=0，根据这个公式直接代入即可得到所求方程．
本题考查了一元二次方程的应用，熟记以x1，x2为根的一元二次方程为x2-(x1+x2)x+x1x2=0是解题的关键．
7.【答案】C
【解析】解：当BD是AC的垂线时，△BAD∽△CBD．
∵BD⊥AC，
∴∠ADB=∠CDB=90°，
∵∠ABC=90°，
∴∠A+∠ABD=∠ABD+∠CBD=90°，
∴∠A=∠CBD，
∴△BAD∽△CBD．
根据作图痕迹可知，
A选项中，BD是∠ABC的平分线，不与AC垂直，不符合题意；
B选项中，BD是AC边上的中线，不与AC垂直，不符合题意；
C选项中，BD是AC的垂线，符合题意；
D选项中，AB=AD，BD不与AC垂直，不符合题意．
故选：C．
若△BAD∽△CBD，可得∠ADB=∠BDC=90°，即BD是AC的垂线，根据作图痕迹判断即可．
本题考查尺规作图、相似三角形的判定，熟练掌握相似三角形的判定是解答本题的关键．
8.【答案】A
【解析】解：由图形知，⑤中∠AHG=135°，
而①②③④中，只有①∠BAC=135°和③∠ADE=135°，
再根据两边成比例可判断，与⑤相似的三角形是①③，
故选：A．
根据相似三角形的旋转可知，相似三角形的对应角相等即可判断．
本题主要考查了相似三角形的判定，熟练掌握两个相似三角形的判定定理是解题的关键．
9.【答案】B
【解析】解：连接AC、CF，如图：

∵四边形ABCD和四边形CEFG是正方形，
∴∠ACG=45°，∠FCG=45°，
∴∠ACF=90°，
∵BC=8，CE=4，
∴AC=82，CF=42，
由勾股定理得，AF=160=410，
∵H是AF的中点，∠ACF=90°，
∴CH=12AF=210，
故选：B．
连接AC、CF，根据正方形的性质得到∠ACF=90°，根据勾股定理求出AF的长，根据直角三角形中，斜边上的中线等于斜边的一半计算即可．
本题考查了直角三角形的性质、勾股定理的应用、正方形的性质，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．
10.【答案】A
【解析】解：连接DF，
∵DE=2AE，
∴S△FDE=2S△FAE，S△CDE=2S△CAE，
∵CD=3BD，
∴S△CDF=3S△BDF，S△ACD=3S△ABD，
∵△ABC的面积等于40cm2，
∴S△ACD=34S△ABC=30cm2，S△ABD=14S△ABC=10cm2，
∴S△CDE=23S△ACD=20cm2，S△CAE=13S△ACD=10cm2，
设S△FAE=x，S△FBD=y，
则S△FDE=2S△FAE=2x，
∴3y=2x+203x+y=10，
解得x=1011y=8011，
∴四边形BDEF的面积为S△ABD-S△FAE=10-1011=10011(cm2).
故选：A．
连接DF，根据DE=2AE，CD=3BD，可知S△FDE=2S△FAE，S△CDE=2S△CAE，S△CDF=3S△BDF，S△ACD=3S△ABD，根据△ABC的面积等于40cm2即可得出S△ACD=34S△ABC=30cm2，S△ABD=14S△ABC=10cm2，S△CDE=23S△ACD=20cm2，S△CAE=13S△ACD=10cm2，根据面积列出方程解出△AEF的面积即可解答．
本题考查的是三角形面积的计算，熟知当高相等时底边之比等于三角形面积之比是解答此题的关键．
11.【答案】8
【解析】解：∵2x=3y，
∴x=1.5y，
∴y+2xx-y=y+3y1.5y-y=4y0.5y=8，
故答案为：8．
根据已知可得x=1.5y，然后代入式子中进行计算即可解答．
本题考查了比例的性质，准确熟练地进行计算是解题的关键．
12.【答案】3-52
【解析】解：设AB=1m，
∵AC：CB=CB：AB，
∴AC：(1-AC)=(1-AC)：1，
∴AC=3-52，
故答案为：3-52．
根据图示得出AC的长即可．
此题考查比例线段，关键是根据比例线段得出方程解答．
13.【答案】-1
【解析】
【分析】
本题考查了一元二次方程的概念，属于基础题，关键是掌握一元二次方程是只含有一个未知数，并且未知数的最高次数是2的整式方程．
根据一元二次方程的定义，只含有一个未知数，并且未知数的最高次数是2，列出方程m2+1=2，且m-1≠0，继而即可得出m的值．
【解答】
解：由一元二次方程的定义得：m2+1=2，且m-1≠0，
解得：m=-1．
故答案为：-1．
14.【答案】11或13
【解析】解：已知等式变形得：(a2-6a+9)+(b2-10b+25)=0，
即(a-3)2+(b-5)2=0，
∵(a-3)2≥0，(b-5)2≥0，
∴a-3=0，b-5=0，
解得：a=3，b=5，
当3是腰时，三边长为3，3，5，符合三角形三边关系，周长为3+3+5=11；
当3是底边时，三边长为3，5，5，符合三角形三边关系，周长为3+7+7=13．
则这个三角形的周长为11或13．
故答案为：11或13．
已知等式配方变形后，利用非负数的性质求出a与b的值，即可确定出等腰三角形周长．
此题考查了配方法的应用，非负数的性质，三角形三边关系，以及等腰三角形的性质，熟练掌握完全平方公式是解本题的关键．
15.【答案】②④
【解析】解：∵矩形ABCD和矩形AEFG，AD=12，AB=9，AG=8，AE=6，
∴∠DAB=∠GAE=90°，AGAD=23，AEAB=23，
∴∠DAG=∠BAE，AGAD=AEAB，
∴△ADG∽△ABE，
∴BEDG=AEAB=23，
∴3BE=DG，故①错误；
如图：设BE与DG交于点H，

∵△ADG∽△ABE，
∴∠AEB=∠AGD，
又∵∠AOE=∠GOH，
∴∠EAO=∠GHO=90°，
∴BE⊥DG，故②正确；
如图，连接BD，GE，DE，BG，

∵AD=12，AB=9，AG=8，AE=6，
∴BD2=AB2+AD2=81+144=225，GE2=AE2+AG2=100，
∵BE⊥DG，
∴BH2+DH2=BD2，BH2+HG2=BG2，HG2+HE2=GE2，DH2+HE2=DE2，
∴BD2+GE2=BG2+DE2，
∴BG2+DE2=325，故③错误；
如图，过点G作GN⊥AB于N，GP⊥直线AD于P，

∵∠BAP=90°，
∴四边形APGN是矩形，
∴AN=GP，NG=AP，
∵∠BAG=60°，
∴∠GAP=30°，
∴GP=12AG=4，AP=3PG=43，
∴S△ABG=12×AB⋅NG=12×9×43=183，S△ADG=12×AD⋅GP=12×12×4=24，
∴4S△ABG=33S△ADG.故④正确；
故答案为：②④．
通过证明△ADG∽△ABE，由相似三角形的性质可求3BE=DG，故①错误；由相似三角形的性质可得∠AEB=∠AGD，由余角的性质可证BE⊥DG，故②正确；由勾股定理可求BG2+DE2=325，故③错误；分别求出S△ABG，S△ADG，即可判断④，即可求解．
本题是四边形综合题，考查了矩形的判定和性质，相似三角形的判定和性质，勾股定理，直角三角形的性质等知识，灵活运用这些性质解决问题是解题的关键．
16.【答案】解：(1)x2+4x-1=0，
x2+4x+4=5，
(x+2)2=5，
x+2=±5，
所以x1=-2+5，x2=-2-5；
(2)3x(x-1)=(1-x)2，
3x(x-1)-(x-1)2=0，
(x-1)(3x-x+1)=0，
x-1=0或3x-x+1=0，
所以x1=1，x2=-12．
【解析】(1)利用配方法得到(x+2)2=5，然后利用直接开平方法解方程；
(2)先移项得到3x(x-1)-(x-1)2=0，再利用因式分解法把方程转化为x-1=0或3x-x+1=0，然后解一次方程即可．
本题考查了解一元二次方程-因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．也考查了配方法．
17.【答案】40 108 45%
【解析】解：(1)这次调查的总人数为6÷15%=40(人)，
扇形统计图中，B类扇形的圆心角为1240×360°=108°，
C类的学生人数为40-6-12-4=18(人)，
∴C类扇形所占的百分比为1840×100%=45%．
故答案为：40；108；45%．
(2)画树状图如下：

共有12种等可能的结果，其中所抽取的2名学生恰好是1名男生和1名女生的结果有8种，
∴所抽取的2名学生恰好是1名男生和1名女生的概率为812=23．
(1)用A类学生人数除以所占百分比可得这次调查的总人数；用B类学生人数除以总人数再乘以360°，即可得B类扇形的圆心角；先求出C类学生人数，进而可得C类扇形所占的百分比．
(2)画树状图得出所有等可能的结果数和所抽取的2名学生恰好是1名男生和1名女生的结果数，再利用概率公式可得出答案．
本题考查列表法与树状图法、条形统计图、扇形统计图，能够读懂条形统计图和扇形统计图，掌握列表法与树状图法以及概率公式是解答本题的关键．
18.【答案】(3,6) 1：2
【解析】解：(1)如图，△A1B1C1为所作；
(2)如图，△A2B2C2为所作；

(3)点A2的坐标为(3,6)，
∵△ABC沿x轴翻折后的△A1B1C1，
∴△ABC≌△A1B1C1，
∵△A1B1C1按2：1放大后的位似图形△A2B2C2，
∴△A1B1C1与△A2B2C2的相似比为1：2，
∴△ABC与△A2B2C2的相似比为1：2，
∴△ABC与△A2B2C2的周长的比为1：2．
(1)利用关于x轴对称的点的坐标特征得到A1、B1、C1的坐标，然后描点即可；
(2)延长MA1到A2使MA2=2MA1，延长MB1到B2使MB2=2MB1，延长MC1到C2使MC2=2MC1，从而得到△A2B2C2；
(3)先利用轴对称的性质得到△ABC≌△A1B1C1，再根据位似的性质得到△A1B1C1与△A2B2C2的相似比为1：2，所以△ABC与△A2B2C2的相似比为1：2，然后根据相似三角形的性质解决问题．
本题考查了作图-位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k.也考查了轴对称变换．
19.【答案】(1)证明：∵四边形ABCD是矩形，
∴AD/​/BC，
∴∠MDO=∠BNO，
∵对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，
∴BM=DM，BO=DO，
在△MDO和△NBO中，
∠MOD=∠NOBDO=BO∠MDO=∠NBO，
∴△MDO≌△NBO(ASA)，
∴MD=BN，
∵AD/​/BC，
∴四边形BMDN是平行四边形，
∵BM=DM，
∴四边形BMDN是菱形；
(2)解：∵四边形ABCD是矩形，
∴∠A=90°，
由勾股定理得：AB2+AM2=BM2，
∵AB=4，AD=8，
∴42+AM2=(8-AM)2，
解得：AM=3，
∴DM=5，
∴△BMD的面积=12×DM×AB=12×5×4=10．
【解析】(1)根据矩形的性质得出AD//BC，根据平行线的性质得出∠MDO=∠BNO，根据线段垂直平分线性质得出BM=DM，BO=DO，根据全等三角形的判定定理得出△MDO≌△NBO，根据全等三角形的性质得出MD=BN，再根据菱形的判定推出即可；
(2)根据矩形的性质得出∠A=90°，根据勾股定理得出AB2+AM2=BM2，求出AM，求出DM，再根据三角形的面积公式求出答案即可．
本题考查了矩形的性质，菱形的判定，勾股定理，线段垂直平分线性质和全等三角形的性质和判定等知识点，能熟记矩形的性质是解此题的关键，矩形的四个角都是直角，矩形的对边平行．
20.【答案】解：(1)设月销售量y与销售单价x之间的函数关系式为y=kx+b(k≠0)，
将(28,60)，(32,40)代入y=kx+b得：28k+b=6032k+b=40，
解得：k=-5b=200，
∴月销售量y与销售单价x之间的函数关系式为y=-5x+200．
(2)依题意得：(x-25)(-5x+200)=70，
整理得：x2-65x+1014=0，
解得：x1=26，x2=39(不符合题意，舍去)．
答：该设备的销售单价应是26万元/台．
【解析】(1)观察函数图象，根据图象上点的坐标，利用待定系数法即可求出y与x之间的函数关系式；
(2)利用月利润=每台的销售利润×月销售量，即可得出关于x的一元二次方程，解之取其符合题意的值即可得出结论．
本题考查了一元二次方程的应用以及一次函数的应用，解题的关键是：(1)利用待定系数法，求出y与x之间的函数关系式；(2)找准等量关系，正确列出一元二次方程．
21.【答案】解：(1)CF与BD位置关系是垂直；
证明如下：
∵AB=AC，∠ACB=45°，
∴∠ABC=45°．
由正方形ADEF得AD=AF，
∵∠DAF=∠BAC=90°，
∴∠DAB=∠FAC，
∴△DAB≌△FAC(SAS)，
∴∠ACF=∠ABD．
∴∠BCF=∠ACB+∠ACF=90°．
即CF⊥BD；
(2)AB≠AC时，CF⊥BD的结论成立．
理由是：
过点A作GA⊥AC交BC于点G，
∵∠ACB=45°，
∴∠AGD=45°，
∴AC=AG，
同理可证：△GAD≌△CAF
∴∠ACF=∠AGD=45°，∠BCF=∠ACB+∠ACF=90°，
即CF⊥BD；
(3)过点A作AQ⊥BC交CB的延长线于点Q，
①点D在线段BC上运动时，
∵∠BCA=45°，可求出AQ=CQ=4．
∴DQ=4-x，△AQD∽△DCP，
∴CPDQ=CDAQ，
∴CP4-x=x4，
∴CP=-x24+x．
②点D在线段BC延长线上运动时，
∵∠BCA=45°，
∴AQ=CQ=4，
∴DQ=4+x．
过A作AQ⊥BC，
∴∠Q=∠FAD=90°，
∵∠C'AF=∠C'CD=90°，∠AC'F=∠CC'D，
∴∠ADQ=∠AFC'，∠P=∠AFC'，
则△AQD∽△AC'F．
∴CF⊥BD，
∴△AQD∽△DCP，
∴CPDQ=CDAQ，
∴CP4+x=x4，
∴CP=x24+x．
【解析】(1)由∠ACB=45°，AB=AC，得∠ABD=∠ACB=45°；∴∠BAC=90°，由正方形ADEF，可得∠DAF=90°，AD=AF，∠DAF=∠DAC+∠CAF；∠BAC=∠BAD+∠DAC；∴∠CAF=∠BAD.可证△DAB≌△FAC(SAS)，得∠ACF=∠ABD=45°，∴∠BCF=∠ACB+∠ACF=90°.即CF⊥BD；
(2)过点A作AG⊥AC交BC于点G，可得出AC=AG，易证：△GAD≌△CAF，所以∠ACF=∠AGD=45°，∠BCF=∠ACB+∠ACF=90°.即CF⊥BD；
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P，设AC=42，BC=3，CD=x，求线段CP的长．考虑点D的位置，分两种情况去解答．①点D在线段BC上运动，已知∠BCA=45°，可求出AQ=CQ=4.即DQ=4-x，易证△AQD∽△DCP，∴CPDQ=CDAQ，∴CP4-x=x4，问题可求．②点D在线段BC延长线上运动时，∵∠BCA=45°，可求出AQ=CQ=4，∴DQ=4+x.过A作AQ⊥BC交CB延长线于点Q，则△AQD∽△AC'F，得CF⊥BD，由△AQD∽△DCP，得CPDQ=CDAQ，∴CP4+x=x4，问题解决．
此题综合性强，须运用所学全等、相似、正方形等知识点，属能力拔高性的类型．
22.【答案】问题背景
证明：∵△ABC∽△ADE，
∴ABAD=ACAE，∠BAC=∠DAE，
∴∠BAD=∠CAE，ABAC=ADAE，
∴△ABD∽△ACE；
尝试应用
解：如图1，连接EC，
∵∠BAC=∠DAE=90°，∠ABC=∠ADE=30°，
∴△ABC∽△ADE，
由(1)知△ABD∽△ACE，
∴AEEC=ADBD=3，∠ACE=∠ABD=∠ADE，
在Rt△ADE中，∠ADE=30°，
∴ADAE=3，
∴ADEC=ADAE×AECE=3×3=3．
∵∠ADF=∠ECF，∠AFD=∠EFC，
∴△ADF∽△ECF，
∴DFCF=ADCE=3．
拓展创新
解：如图2，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，
∵∠BAD=30°，
∴∠DAM=60°，
∴∠AMD=30°，
∴∠AMD=∠DBC，
又∵∠ADM=∠BDC=90°，
∴△BDC∽△MDA，
∴BDMD=DCDA，
又∵∠BDC=∠ADM，
∴∠BDC+∠CDM=∠ADM+∠CDM，
即∠BDM=∠CDA，
∴△BDM∽△CDA，
∴BMCA=DMAD=3，
∵AC=23，
∴BM=23×3=6，
∴AM=BM2-AB2=62-42=25，
∴AD=12AM=5．
【解析】此题是相似形综合题，考查了直角三角形的性质，勾股定理，相似三角形的判定与性质等知识，熟练掌握相似三角形的判定与性质是解题的关键．
问题背景
由题意得出ABAD=ACAE，∠BAC=∠DAE，则∠BAD=∠CAE，可证得结论；
尝试应用
连接EC，证明△ABC∽△ADE，由(1)知△ABD∽△ACE，由相似三角形的性质得出AEEC=ADBD=3，∠ACE=∠ABD=∠ADE，可证明△ADF∽△ECF，得出DFCF=ADCE=3，则可求出答案．
拓展创新
过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，证明△BDC∽△MDA，由相似三角形的性质得出BDMD=DCDA，证明△BDM∽△CDA，得出BMCA=DMAD=3，求出BM=6，由勾股定理求出AM，最后由直角三角形的性质可求出AD的长．