











- 专题01 实数 题型归纳+课件 课件 36 次下载
- 专题02 整式 题型归纳+课件 课件 32 次下载
- 专题04 一次方程与方程组 题型归纳+课件 课件 33 次下载
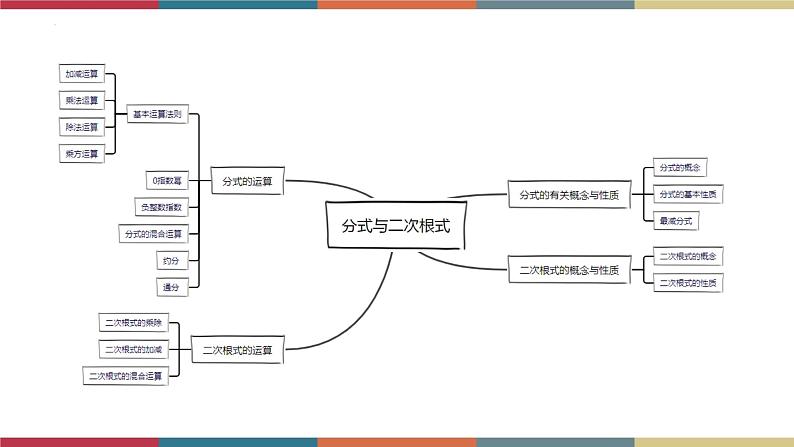
专题03 分式与二次根式 题型归纳+课件
展开When you click on the title, you will enter the content of the speech.Please listen quietly. Detailed presentations on each project will be followed by an answer time.
考点1:分式的有关概念及性质
分最简分式:分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式,要进行约分化简.
考点2:分式的运算
(4)乘方运算:分式的乘方,把分子分母分别乘方.
分式的混合运算顺序:先算乘方,再算乘除,最后加减,有括号先算括号里面的.
约分:把一个分式的分子和分母的公因式约去,这种变形称为分式的约分.
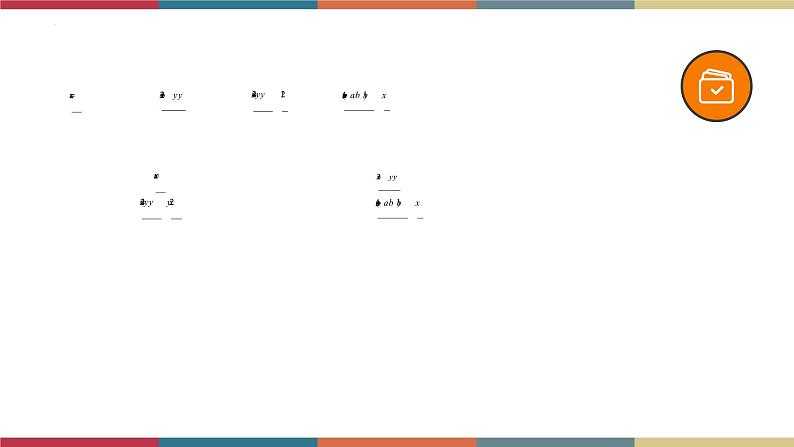
通分:根据分式的基本性质,异分母的分式可以化为同分母的分式,这一过程称为分式的通分.
约分需明确的问题:(1)对于一个分式来说,约分就是要把分子与分母都除以同一个因式,使约分前后分式的值相等;(2)约分的关键是确定分式的分子和分母的公因式,其思考过程与分解因式中提取公因式时确定公因式的思考过程相似;在此,公因式是分子、分母系数的最大公约数和相同字母最低次幂的积.
通分注意事项:(1)通分的关键是确定最简公分母;最简公分母应为各分母系数的最小公倍数与所有因式的最高次幂的积.(2)不要把通分与去分母混淆,本是通分,却成了去分母,把分式中的分母丢掉.(3)确定最简公分母的方法:最简公分母的系数,取各分母系数的最小公倍数;最简公分母的字母,取各分母所有字母因式的最高次幂的积.
考点3:二次根式的主要性质
积的算术平方根的性质:
商的算术平方根的性质:
考点4:二次根式的运算
二次根式的乘除运算(1)运算结果应满足以下两个要求:①应为最简二次根式或有理式;②分母中不含根号.(2)注意知道每一步运算的算理;
二次根式的加减运算:先化为最简二次根式,再类比整式加减运算,明确二次根式加减运算的实质;
二次根式的混合运算(1)对二次根式的混合运算首先要明确运算的顺序,即先乘方、开方,再乘除,最后算加减,如有括号,应先算括号里面的;(2)二次根式的混合运算与整式、分式的混合运算有很多相似之处,整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用.
怎样快速准确地进行二次根式的混合运算.1.明确运算顺序,先算乘方,再算乘除,最后算加减,有括号先算括号里面的;2.在二次根式的混合运算中,原来学过的运算律、运算法则及乘法公式仍然适用;3.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能收到事半功倍的效果.(1)加法与乘法的混合运算,可分解为两个步骤完成,一是进行乘法运算,二是进行加法运算,使难点分散,易于理解和掌握.在运算过程中,对于各个根式不一定要先化简,可以先乘除,进行约分,达到化简的目的,但最后结果一定要化简.(2)多项式的乘法法则及乘法公式在二次根式的混合运算中同样适用.
温馨提示:
易错易混知识点
1.分式值为0时,忽略分母不为0的条件分式的值为0,必须同时满足两个条件,即分子的值为0,分母不等于0,两者缺一不可。2.在分式约分过程中出现乱约分或约分不彻底的错误分式的约分是对分式的分子与分母整体进行的,分子或分母必须都是乘积的形式才能进行约分,约分要彻底,使分子、分母没有公因式。
易错易混知识点
3.分式运算时忽视分数线的括号作用在分式的运算中遇到减法,并且减式的分子是一个多项式,当分子相减时必须给分子加上括号,因为分数线有括号的作用。4.对二次根式的定义理解不透,认为只要带二次根号即为二次根式,忽视了二次根式 中a≥0的条件,所以在平时做题中必须特别注意理解二次根式的被开方数是非负数。
易错易混知识点
强化训练
谢谢观看!
专题03 分式与二次根式(精品课件)-备战2023年中考数学一轮复习精品课件与题型归纳专练(全国通用): 这是一份专题03 分式与二次根式(精品课件)-备战2023年中考数学一轮复习精品课件与题型归纳专练(全国通用),共53页。PPT课件主要包含了考点2分式的运算,温馨提示,易错易混知识点,强化训练等内容,欢迎下载使用。
2023年中考数学一轮复习精品课件专题03 分式与二次根式: 这是一份2023年中考数学一轮复习精品课件专题03 分式与二次根式,共53页。PPT课件主要包含了考点2分式的运算,温馨提示,易错易混知识点,强化训练等内容,欢迎下载使用。
专题02 整式 题型归纳+课件: 这是一份专题02 整式 题型归纳+课件,文件包含专题02整式精品课件pptx、专题02整式题型归纳解析版docx、专题02整式题型归纳原卷版docx等3份课件配套教学资源,其中PPT共45页, 欢迎下载使用。












