

2022-2023学年福建省泉州市南安市七年级(上)期中数学试卷(含解析)
展开
这是一份2022-2023学年福建省泉州市南安市七年级(上)期中数学试卷(含解析),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省泉州市南安市七年级(上)期中数学试卷 一、选择题(本大题共10小题,共40分) 的相反数是( )A. B. C. D. 的绝对值是( )A. B. C. D. 在,,,,中,整数的个数是( )A. B. C. D. 如果家用电冰箱冷藏室的温度是,冷冻室的温度比冷藏室的温度低,那么冷冻室的温度是( )A. B. C. D. 下列运算正确的是( )A. B. C. D. 年月日,“天宫课堂”再度开课,三位“太空教师”翟志刚、王亚平、叶光富在距离地球约米的中国空间站为广大青少年带来了一场精彩的太空科普课,数字用科学记数法表示为( )A. B. C. D. 下列说法中正确的是( )A. 一定是负数
B. 若一个数的平方是它本身,则这个数是或
C. 是最小的整数
D. 分数不是有理数 某快递公司受新一次疫情影响,月份业务量比月份下降了,由于采取了科学的防控措施,月份疫情明显好转,该快递公司月份业务量比月份增长了,若设该快递公司月份业务量为,则月份的业务量为( )A. B.
C. D. 若数,在数轴上的对应点的位置如图所示,则以下结论正确的是( )
A. B. C. D. 若记,并且表示当时的值,即,表示当时的值,即,则( )A. B. C. D. 二、填空题(本大题共6小题,共24分)负数的概念最早出现在中国古代著名的数学专著九章算术中,负数与对应的正数“数量相等,意义相反”,如果向东走米,记作米,那么向西走米,可记作______米.有理数精确到百分位的结果为______.若,则的值为______.支签字笔元,一支铅笔元,支签字笔和支铅笔共需要______元.如图,第个图形中有个三角形,第个图形中有个三角形,第个图形中有个三角形则第个图形中有______个三角形.
如图,三个形状、大小都相同的小长方形沿“横竖横”排列在一个大长方形中,若一个小长方形的周长为,则这个大长方形的周长为______.
三、解答题(本大题共9小题,共86分)把下列各数填在相应的集合内:,,,,,.,.
分数集合:______;
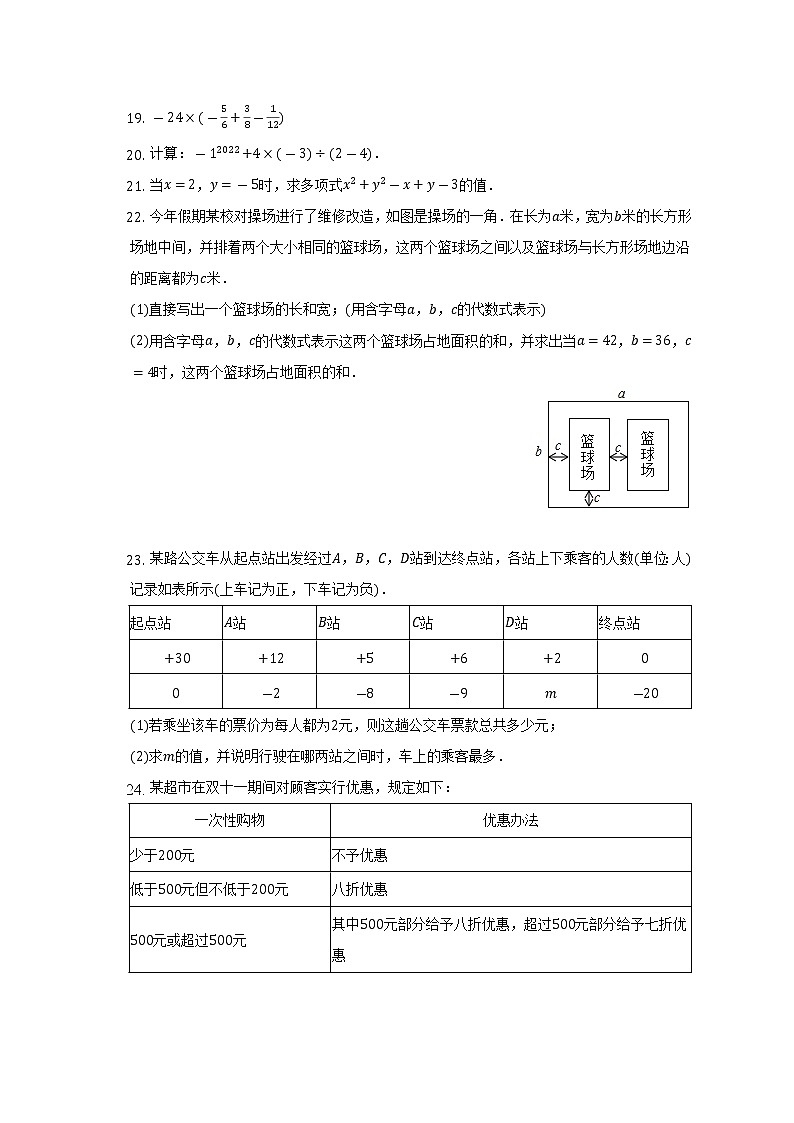
负有理数集合:______.计算:.计算:.当,时,求多项式的值.今年假期某校对操场进行了维修改造,如图是操场的一角.在长为米,宽为米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为米.
直接写出一个篮球场的长和宽;用含字母,,的代数式表示
用含字母,,的代数式表示这两个篮球场占地面积的和,并求出当,,时,这两个篮球场占地面积的和.
某路公交车从起点站出发经过,,,站到达终点站,各站上下乘客的人数单位:人记录如表所示上车记为正,下车记为负.起点站站站站站终点站若乘坐该车的票价为每人都为元,则这趟公交车票款总共多少元;
求的值,并说明行驶在哪两站之间时,车上的乘客最多.某超市在双十一期间对顾客实行优惠,规定如下:一次性购物优惠办法少于元不予优惠低于元但不低于元八折优惠元或超过元其中元部分给予八折优惠,超过元部分给予七折优惠若王老师一次性购物元,他实际付款______元.若王老师实际付款元,那么王老师一次性购物可能是______元;
若顾客在该超市一次性购物元,当小于元但不小于时,他实际付款______元,当大于或等于元时,他实际付款______元用含的代数式表示;
如果王老师有两天去超市购物原价合计元,第一天购物的原价为元,用含的代数式表示这两天购物王老师实际一共付款多少元?当元时,王老师两天一共节省了多少元?阅读下面材料:如图,点、在数轴上分别表示有理数,,则、两点之间的距离可以表示为.
根据阅读材料与你的理解回答下列问题:
数轴上表示与的两点之间的距离是______;
若,则______;若,则______;
表示数轴上有理数所对的点到和所对的两点距离之和,请你利用数轴,写出所有符合条件的整数,使得.
若表示一个有理数,则有最小值吗?若有,请直接写出最小值.若没有,说出理由.
答案和解析 1.【答案】 【解析】解:的相反数是,
故选:.
根据相反数的定义直接求解.
本题主要考查相反数的定义,熟练掌握相反数的定义是解答此题的关键.
2.【答案】 【解析】解:,
故选:.
根据负数的绝对值等于它的相反数即可得出答案.
本题考查了绝对值,掌握负数的绝对值等于它的相反数是解题的关键.
3.【答案】 【解析】解:在,,,,中,整数有,,,共个.
故选:.
根据有理数的分类解答即可.
此题考查了有理数,熟知整数包括正整数、和负整数是解答本题的关键.
4.【答案】 【解析】解:根据题意得:,
则这台电冰箱冷冻室的温度为.
故选:.
根据题意列出算式,再根据有理数的减法法则计算即可,有理数减法法则:减去一个数,等于加上这个数的相反数.
此题考查了有理数的减法,弄清题意并掌握有理数的减法法则是解本题的关键.
5.【答案】 【解析】解:、原式,不符合题意;
B、原式,不符合题意;
C、原式,符合题意;
D、原式,不符合题意.
故选:.
根据有理数的运算法则计算可得出结果.
本题主要考查有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和运算法则.
6.【答案】 【解析】解:.
故选:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
7.【答案】 【解析】解:、一定是负数,错误,例如,是正数,故本选项错误;
B、若一个数的平方是它本身,则这个数是或,故本选项正确;
C、没有最小的整数,故本选项错误;
D、分数是有理数,故本选项错误.
故选:.
根据负数,整数以及乘方的运算对各选项分析判断即可得解.
本题考查了有理数,正数和负数,掌握相关观念是解题的关键.
8.【答案】 【解析】解:该快递公司月份业务量为,月份业务量比月份下降了,
月份业务量是,
月份业务量比月份增长了,
月份业务量是,
故选:.
先表示出月份业务量是,再根据月份业务量比月份增长了,即可列出代数式.
此题考查了列代数式,关键是读懂题意,找出题目中的数量关系,列出代数式.
9.【答案】 【解析】解:由数轴知,,,
正确,选项A符合题意;
,选项B不符合题意;
,选项C不符合题意;
,选项D不符合题意.
故选:.
判断出两个点表示的数,直接比较大小即可.
本题考查的是实数的大小比较,绝对值,乘法与减法法则,解题的关键是从数轴上找出这两个数.
10.【答案】 【解析】解:,
,
,
故选:.
根据所给的式子,通过计算可得,再利用该结论求解即可.
本题考查数字的变化规律,通过计算,探索出是解题的关键.
11.【答案】 【解析】解:因为向东和向西是具有相反的意义,向东记作正数,则向西就记作负数.
故正确答案为:.
利用正负数可以表示具有相反意义的量.
本题考查正负数的意义,即:正负数可以表示具有相反意义的量.
12.【答案】 【解析】解:有理数精确到百分位的结果为.
故答案为:.
把千分位上的数字进行四舍五入即可.
本题考查了近似数:“精确到第几位”是精确度的常用的表示形式.
13.【答案】 【解析】解:,
,,
,,
.
故答案为:.
根据非负数的性质求出和的值,再代入所求代数式进行计算即可.
本题考查的是非负数的性质,即几个非负数的和为时,这几个非负数都为.
14.【答案】 【解析】解:元,
故答案为:.
根据总价单价数量,分别求出签字笔和铅笔的总价,再相加即可.
本题主要考查列代数式,解答本题的关键是准确掌握单价、总价和数量之间的关系.
15.【答案】 【解析】解:第个图形中一共有个三角形,
第个图形中一共有个三角形,
第个图形中一共有个三角形,
第个图形中三角形的个数是,
当时,,
第个图形中有个三角形.
故答案为:.
根据题目中的图形,可以发现三角形个数的变化规律:,从而可以解答本题.
本题考查规律型:图形的变化类,解答本题的关键是明确题意,发现题目中的三角形个数的变化规律,利用数形结合的思想解答.
16.【答案】 【解析】解:设小长方形的长为,宽为,则大长方形的长为,宽为,
大长方形的周长为:,
一个小长方形的周长为,
,
,
一个大长方形的周长为:,
故答案为:.
设小长方形的长为,宽为,则大长方形的长为,宽为,根据大长方形的周长得出,再结合小长方形的周长可得:,求出,再求出大长方形的周长即可.
本题考查了图形的变化类和长方形的性质,能熟记长方形的性质是解此题的关键.
17.【答案】,,., ,, 【解析】解:,,,,,.,.
分数集合:.,,;
负有理数集合:.
故答案为:,,.,;,,.
根据有理数的分类解答即可.整数和分数统称为有理数.
本题考查了有理数,掌握有理数的分类是解答本题的关键.
18.【答案】解:
. 【解析】从左向右依次计算,求出算式的值是多少即可.
此题主要考查了有理数的加法的运算方法,以及有理数的混合运算,要熟练掌握,注意运算顺序.
19.【答案】解:,
,
,
,
. 【解析】利用乘法分配律进行计算即可得解.
本题考查了有理数的乘法,利用运算定律可以使计算更加简便.
20.【答案】解:
. 【解析】先算乘方,再算乘除法,最后算加法即可.
本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的运算顺序和运算法则.
21.【答案】解:当,时,
. 【解析】将,代入多项式进行计算即可.
此题考查了求代数式值的计算能力,关键是能代入进行准确计算.
22.【答案】解:一个篮球场的长和宽分别为:,;
这两个篮球场的占地面积为平方米;
当,,时,平方米. 【解析】根据题意求出两个长方形的长和宽,即可;
把,,代入求出即可.
本题考查了求代数式的值和列代数式,能正确根据题意列出代数式是解此题的关键.
23.【答案】解:
元,
答:这趟公交车票款总共元;
起点到站,车上人数:,
站到站,车上人数:,
站到站,车上人数,,
站到点,,
站到终点站,,
解得:,
答:表格中的值是,站与站之间,车上的人数最多,最多乘客人数是人. 【解析】根据各站之间的人数,乘以票价元,然后计算即可得解;
计算各站车上的乘客人数解答即可.
本题考查了正数和负数,有理数的混合运算,读懂图表信息,求出各站点上的人数是解题的关键.
24.【答案】 或 【解析】解:元,
设王老师一次性购物可能是元,
,
根据题意得,,
解得,
,
;
综上所述:王老师一次性购物可能是:元或元.
故答案为:,或;
当小于元但不小于时,他实际付款元,
当大于或等于元时,他实际付款:
元,
故答案为:,;
第一天购物实际付款:元,
第二天购物实际付款:元,
两天共付款:元,
当元时,元,
所以共节省:元.
答:两天购物王老师实际一共付款元,一共节省了元.
元按折计算,超出的折计算;
实际付款元时,设王老师一次性购物可能是元,分两种情况:,按八折计算,,没有折扣;
当小于元但不小于时,他实际付款按折计算,大于或等于元时.他实际付款,这部分按折计算,超出的这部分折计算;
根据的思路表示第一天购物实际付款和第二天购物实际付款.
本题考查了代数式的求值、列代数式,掌握要正确列代数式,只有分清数量之间的关系,表示超出的部分是解题关键.
25.【答案】 或 【解析】解:,
故答案为:;
,
或,
,
,
,
故答案为:或;;
当时,
,
所有符合条件的整数为,,,;
有最小值,
,
当时,有最小值,
最小值为:.
计算即可;
由,即可求解;
由,即可求解;
由条件时,可求解.
本题考查与数轴有关的问题,关键是掌握在数轴上表示两点的距离的方法.
相关试卷
这是一份2023-2024学年福建省泉州市南安市七年级(下)期中数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年福建省泉州市南安市七年级(下)期中数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年福建省泉州市南安市七年级(下)期中数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。








