苏科版九年级下册5.4 二次函数与一元二次方程教学ppt课件

这是一份苏科版九年级下册5.4 二次函数与一元二次方程教学ppt课件，共22页。PPT课件主要包含了情景导入，x百米，你发现了什么，x1＝2x2＝-3，个交点，没有交点，个不相等的实数根，个相等的实数根，没有实数根，图象与x轴的交点个数等内容，欢迎下载使用。

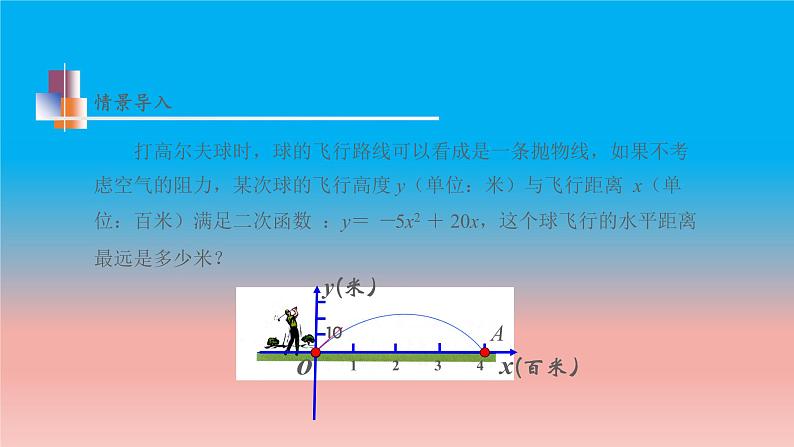
打高尔夫球时，球的飞行路线可以看成是一条抛物线，如果不考虑空气的阻力，某次球的飞行高度 y（单位：米）与飞行距离 x（单位：百米）满足二次函数 ：y＝ －5x2 ＋ 20x，这个球飞行的水平距离最远是多少米？
二次函数与相应的一元二次方程的关系
解：二次函数y=x2-2x-3的图象如图所示.图象与x轴两个交点为M(－1，0)，N（3，0).
由上可知，当x=-1时，y=0，即x2-2x-3=0；所以x=-1是一元二次方程x2-2x-3=0的一个根；同理，当x=3时，y=0，即x2-2x-3=0.所以x=3是一元二次方程x2-2x-3=0的另一个根.
解：令y=0，即x2＋4x-5＝0， 解得，x1＝ －5 ，x2 ＝ 1，∴二次函数y＝x2＋4x－5的图象与x轴的交点坐标为：（－5，0），（1，0）
（2，0），（-3，0）
二次函数与x轴的交点与一元二次方程根的关系
二次函数y=ax2 ＋ bx ＋ c
一元二次方程ax2 ＋ bx＋c＝0
解：因为一元二次方程-x2+5x-8=0的根的判别式b2-4ac=52-4×（-1）×（-8）<0，所以方程-x2+5x-8=0没有实数根.二次函数y＝-x2+5x-8的图象与x轴没有公共点
由顶点式确定二次函数的表达式
1.已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点坐标为(1，0)，则关于x的一元二次方程x2-3x+m＝0的两实数根是( 　　)A．x1＝1，x2＝－1 B．x1＝1，x2＝2C．x1＝1，x2＝0 D．x1＝1，x2＝3
2.二次函数y=x2-2x+1的图象与x轴的交点情况是( 　　)A．有一个交点 B．有两个交点 C．没有交点 D．无法确定
3.若函数y=x2-2x+b的图象与坐标轴有三个交点，则b的取值范围是(　　)A．b＜1且b≠0 B．b＞1C．0＜b＜1 D．b＜1
解析： 因为函数y=x2-2x+b的图象与坐标轴有三个交点，所以(－2)2－4b＞0，解得b＜1，而b≠0，则b＜1且b≠0.故选A.
4.若抛物线y=x2-6x+m与x轴没有交点，则m的取值范围是________．
6.已知关于x的函数y＝(m2－1)x2－(2m＋2)x＋2的图象与x轴只有一个公共点，求m的值.
解：①当m2－1＝0，且2m＋2≠0，即m＝1时，该函数是一次函数，其图象与x轴只有一个公共点；②当m2－1≠0，即m≠±1时，该函数是二次函数，其图象与x轴只有一个公共点，则b2－4ac＝[－(2m＋2)]2－8(m2－1)＝0，解得m＝3或m＝－1(舍去)．综上所述，m的值是1或3.