2021学年第一章 解直角三角形1.1 锐角三角函数教案配套ppt课件

这是一份2021学年第一章 解直角三角形1.1 锐角三角函数教案配套ppt课件，共34页。PPT课件主要包含了锐角三角函数的定义，做一做，特殊角的三角函数值表等内容，欢迎下载使用。

1.1 锐角三角函数（1）
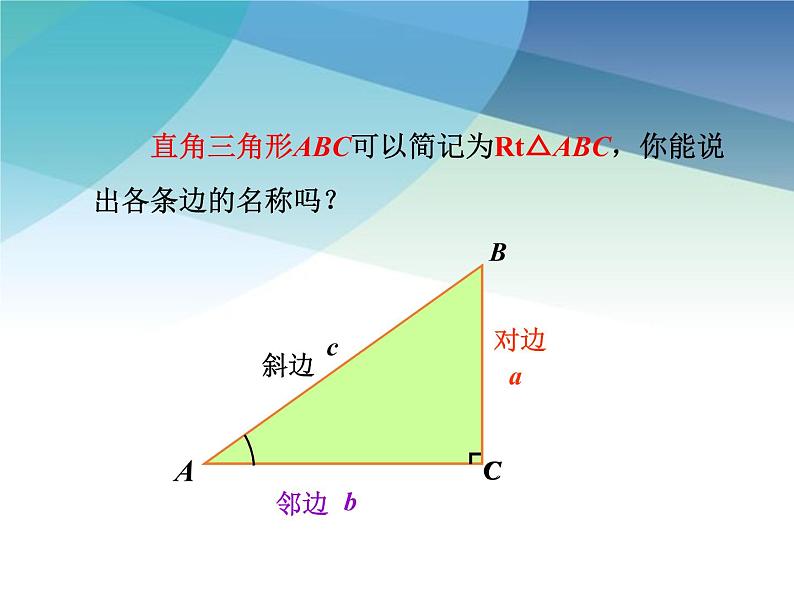
直角三角形ABC可以简记为Rt△ABC，你能说出各条边的名称吗？
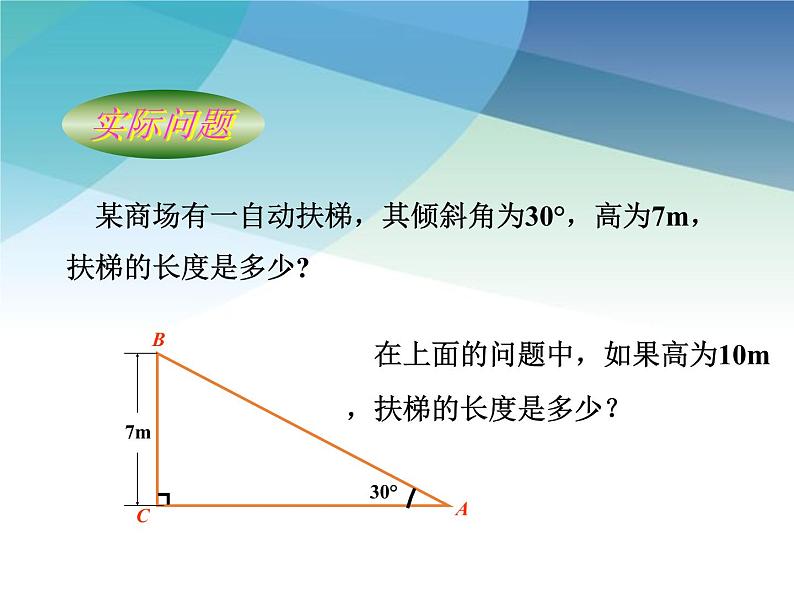
某商场有一自动扶梯，其倾斜角为30°，高为7m，扶梯的长度是多少?
在上面的问题中，如果高为10m ，扶梯的长度是多少？
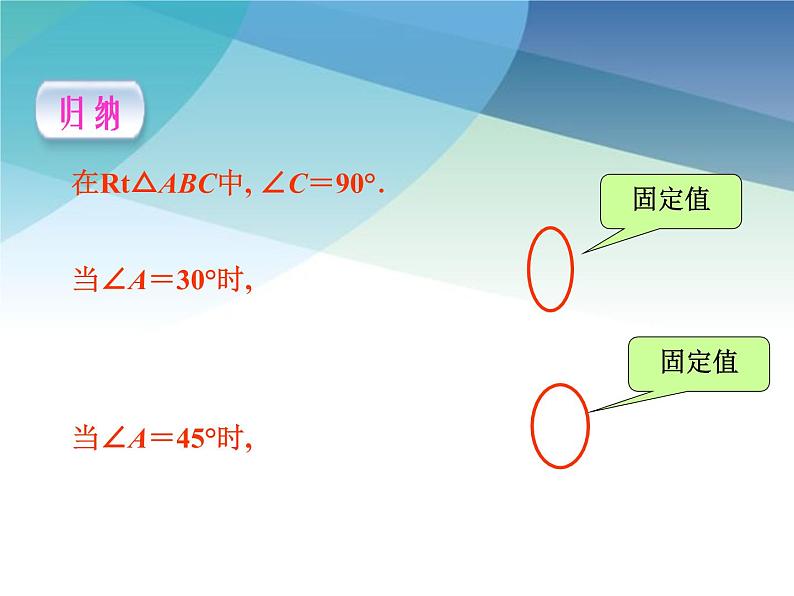
在Rt△ABC中, ∠C＝90°．当∠A＝30°时,当∠A＝45°时,
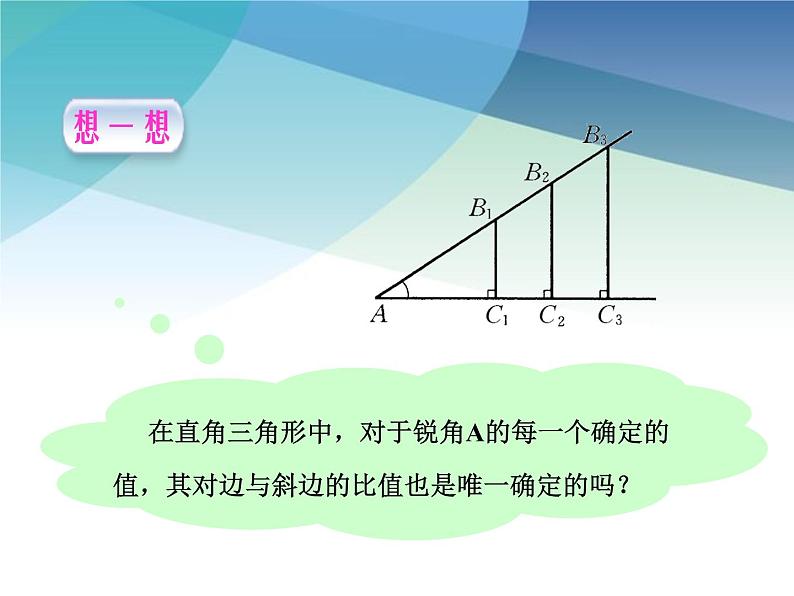
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
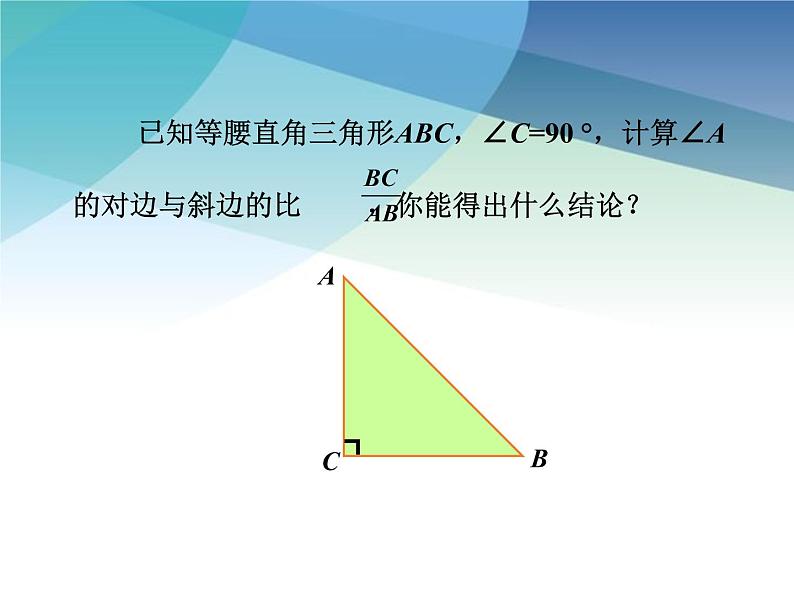
所以，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何， ∠A的对边与斜边的比是一个固定值．
观察右图中的Rt△AB1C1，Rt△AB2C2和Rt△AB3C3，∠A的对边与斜边有什么关系？
在Rt△ABC中， ∠C=90 °，我们把锐角A的对边与斜边的比叫做∠ A的正弦（sine），记作sin A，即
一个角的正弦表示定值、比值、正值．
在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比、∠A的邻边与斜边的比、∠A的对边与邻边的比都是一个固定值．
在Rt△ABC中， ∠C=90 °，我们把锐角A的邻边与斜边的比叫做∠ A的余弦（csine），记作cs A，即
一个角的余弦表示定值、比值、正值．
在Rt△ABC中， ∠C=90 °，我们把锐角A的对边与邻边的比叫做∠ A的正切（tangent），记作tan A，即
一个角的余切表示定值、比值、正值．
锐角三角函数 锐角A的正弦、余弦、正切叫做∠A的锐角三角函数（trignmetric functin f acute angle）
1．sinA，csA，tanA 是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形)． 2．sinA， csA，tanA 是一个比值（数值）． 3．sinA， csA， tanA 的大小只与∠A的大小有关，而与直角三角形的边长无关．
1、如图1，在Rt△MNP中，∠N＝90゜. ∠P的对边是_________,∠P的邻边是___________; ∠M的对边是________,∠M的邻边是___________;
2、设Rt△ABC， ∠C＝90゜ ∠A， ∠B， ∠C的对边分别为a，b，c， a=5，c=13，求∠B的三个三角函数值.
在直角三角形中共有五个元素：边a,b,c, 锐角∠A,∠B.这五个元素之间有如下等量关系：
a2 +b2 =c2 (勾股定理)
1.1 锐角三角函数（2）
30°,45°,60°角的三角函数值
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
直角三角形中边与角的关系:锐角三角函数.
锐角A的正弦、余弦、和正切统称∠A的三角函数
如图,观察一副三角板:它们其中有几个锐角?分别是多少度?
(1)sin300等于多少?
(2)cs300等于多少?
(3)tan300等于多少?
请与同伴交流你是怎么想的?又是怎么做的?
sin 30°=cs 30°=tan 30°=
(4)sin450,sin600等于多少?
(5)cs450,cs600等于多少?
(6)tan450,tan600等于多少?
根据上面的计算,完成<特殊角的三角函数值表>
老师期望:你能对伴随九个学年的这副三角尺所具有的功能来个重新认识和评价.
sin45 ° =cs45°=tan45°=
sin60°=cs60°=tan60°=
这张表还可以看出许多知识之间的内在联系?
例1 计算:(1)sin30°+cs45°;(2) sin260°+cs260°-tan45°.
老师提示:sin260°表示(sin60°)2,cs260°表示(cs60°)2,其余类推.
(1)sin600-cs450; (2)cs600+tan600;
例2 如图,一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
老师提示:将实际问题数学化.
例3 一位同学的手臂长65 cm，当他高举双臂时，指尖高出头顶35 cm。问当他的手臂与水平成角时，指尖高出头顶多少厘米（精确到0.1 cm）？
老师期望:sin2A+cs2A=1它反映了同角之间的三角函数的关系,且它更具有灵活变换的特点,若能予以掌握,则将有益于智力开发.
1.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少?
2.如图,在Rt△ABC中,∠C=90°,∠A,∠B ,∠C的对边分别是a,b,c.求证:sin2A+cs2A=1.
已知∠A为锐角，且csA= ， 你能求出∠A的度数吗?
看图说话:直角三角形三边的关系.直角三角形两锐角的关系.直角三角形边与角之间的关系.特殊角300,450,600角的三角函数值.互余两角之间的三角函数关系.同角之间的三角函数关系
1.计算：(1)tan450-sin300;(2)cs600+sin450-tan300;
2.如图,河岸AD,BC互相平行,桥AB垂直于两岸.桥长12m,在C处看桥两端A,B,夹角∠BCA=600.求B,C间的距离(结果精确到1m).