广东省深圳市南山区中科先进实验学校2022-2023学年上学期七年级期中考试数学试卷(含答案)

这是一份广东省深圳市南山区中科先进实验学校2022-2023学年上学期七年级期中考试数学试卷(含答案)，共11页。试卷主要包含了－的倒数等于，下列各组式子中，为同类项的是，下列说法中正确的是等内容，欢迎下载使用。
南山区中科先进实验学校2022-2023学年第一学期七年级期中考试数学试卷

一．选择题（每题3分，共30分）
1． 在0，﹣2，1，这四个数中，最小的数是（　　）
A．0 B．1 C．﹣2 D．

2． －的倒数等于（　　）
A．3 B．﹣3 C． D．

3． 如图所示，下列四个图形中不是正方体的平面展开图的是（　　）
A． B． C． D．

4． 2021年9月20日“天舟三号”在海南成功发射，这是中国航天工程又一重大突破，它的运行轨道距离地球393000米，数据393000米用科学记数法表示为（　　）
A．0.393×107米 B．3.93×106米 C．3.93×105米 D．39.3×104米

5． 下列各组式子中，为同类项的是（　　）
A．﹣3xy与yx B．﹣4x与4x2 C．5x2y与﹣2xy2 D．3a与3b

6． 如图，下列四个图形是由已知的四个立体图形展开得到的，则对应的标号是（　　）

A．①②③④ B．②①③④ C．③②①④ D．④②①③

7． 若有理数a，b满足|a＋1|+|b﹣3|＝0，则2a+3b的值为（　　）
A．5 B．6 C．7 D．8

8． 下列说法中正确的是（　　）
A．﹣a一定表示负数 B．两个有理数比较大小，绝对值大的反而小
C．如果|a﹣5|＝4，则a必定为9 D．如果|a|＝a，则a必定为正数或零

9． 十位数字是a，个位数字是b的两位数是（　　）
A．ab B．a+10b C．ba D．10a+b

10．有一个数值转换器，原理如图所示，若开始输入x的值是5，可发现第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是4，依次继续下去，第2022次输出的结果是（　　）

A．1 B．2 C．4 D．8

二．填空题（每题3分，共15分）
11．比较大小：﹣3.14　 　﹣π（用“＞”“＜”“＝”连接）．

12．已知单项式﹣3x3yn与5xm+4y3是同类项，则m﹣n的值为　 　．

13．数轴上点A表示﹣2，从A出发，沿数轴移动4个单位长度到达点B，则点B表示的数是　 　．

14．已知2x﹣3y﹣5＝0，则6x﹣9y+15＝　 　．

15．已知a，b，c是三个有理数，它们在数轴上的位置如图所示，化简|a﹣b|+|c﹣a|﹣|b+c|＝　 　．

三．解答题（共55分）
16．（12分）计算与合并同类项：
（1）－23÷×(－)2； （2）(－－)×(－48)；



（3）－22÷(－1)2020－|－7|×5； （4）12－(－18)＋(－7)＋(－12)；



（5）4a2+3b2﹣2ab﹣3a2﹣5b2； （6）2x3﹣6x﹣6x3﹣2+9x+8．



17．（6分）（1）在数轴上表示下列各数：，﹣2，﹣4，3；

（2）请将上面各数用“＜”号连接起来．

18．（6分）砀山酥梨是一种驰名中外的特色水果，它是梨的一种，因为出产于砀山县而得名．现有20筐砀山酥梨，以每筐25千克的质量为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克）
﹣3
﹣2
﹣1.5
0
1
2.5
筐数
1
4
2
3
2
8
（1）这20筐砀山酥梨中，最重的一筐比最轻的一筐重多少千克？
（2）与标准质量比较，这20筐砀山酥梨总计超过或不足多少千克？
（3）若砀山酥梨每千克售价4元，则这20筐砀山酥梨可卖多少元？






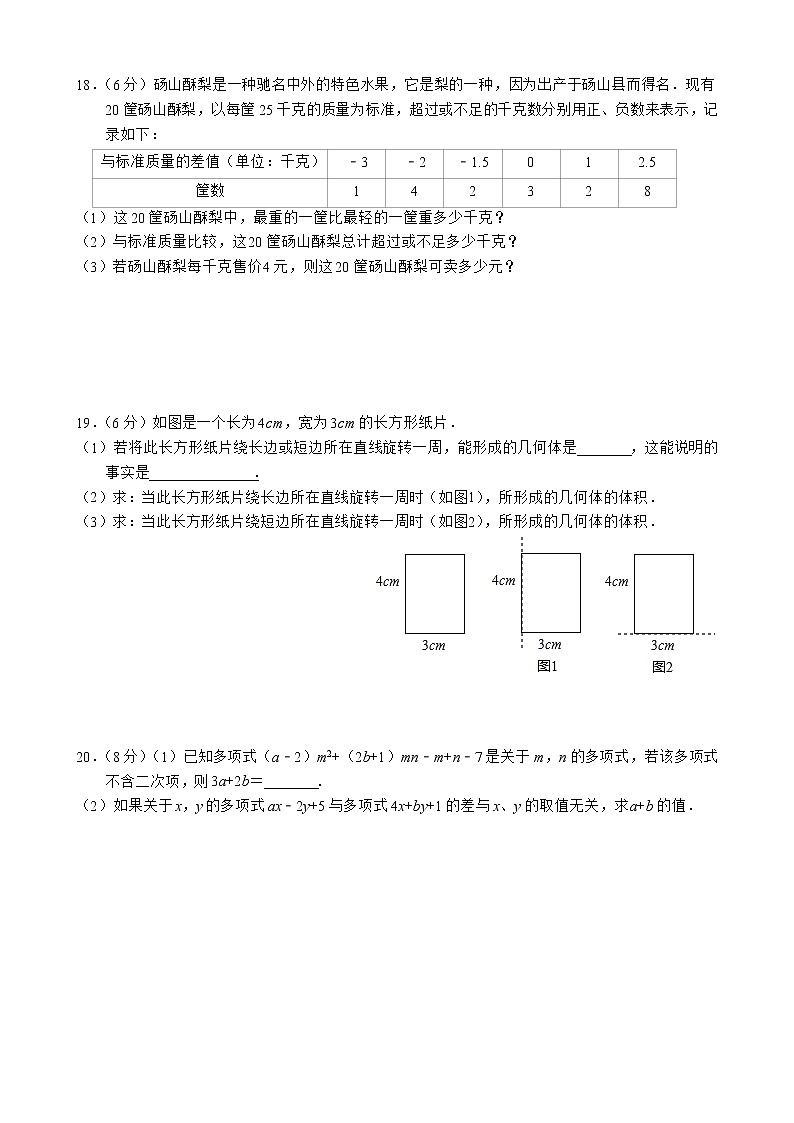
19．（6分）如图是一个长为4cm，宽为3cm的长方形纸片．
（1）若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是_______，这能说明的事实是______________．
（2）求：当此长方形纸片绕长边所在直线旋转一周时（如图1），所形成的几何体的体积．
（3）求：当此长方形纸片绕短边所在直线旋转一周时（如图2），所形成的几何体的体积．




20．（8分）（1）已知多项式（a﹣2）m2+（2b+1）mn﹣m+n﹣7是关于m，n的多项式，若该多项式不含二次项，则3a+2b＝_______．
（2）如果关于x，y的多项式ax﹣2y+5与多项式4x+by+1的差与x、y的取值无关，求a+b的值．






21．（8分）【阅读材料】问题：如何计算呢？小红带领的数学兴趣小组通过探索完成了这道题的计算．
他们的解法如下：
解：原式＝（1﹣）+（）+（）+…+（）＝1﹣＝．
根据材料，请你完成下列计算：
（1）计算：＋；
（2）直接写出结果：＝　 　；
（3）计算：＋．











22．（9分）如图，已知数轴上原点为O，点B表示的数为﹣2，A在B的右边，且A与B的距离是5，动点P从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，动点Q从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，设运动时间为t（t＞0）秒．
（1）写出数轴上点A表示的数　 　，与点A的距离为3的点表示的数是　 　．
（2）点P表示的数　 　（用含t的代数式表示），点Q表示的数　 　（用含t的代数式表示）．
（3）问点P与点Q何时到点O距离相等？


参考答案与试题解析
一．选择题（共10小题）
1．在0，﹣2，1，这四个数中，最小的数是（　　）
A．0 B．1 C．﹣2 D．
【解答】解：∵﹣2＜0＜＜1，
∴最小的数是﹣2，故选：C．
2．－的倒数等于（　　）
A．3 B．﹣3 C． D．
【解答】解：∵－3×－＝1，
∴－的倒数等于－3．故选：B．
3．如图所示，下列四个图形中不是正方体的平面展开图的是（　　）
A． B． C． D．
【解答】解：由四棱柱四个侧面和上下两个底面的特征可知B，C、D选项可以拼成一个正方体，而A选项，上底面不可能有两个，故不是正方体的展开图．
故选：A．
4．2021年9月20日“天舟三号”在海南成功发射，这是中国航天工程又一重大突破，它的运行轨道距离地球393000米，数据393000米用科学记数法表示为（　　）
A．0.393×107米 B．3.93×106米 C．3.93×105米 D．39.3×104米
【解答】解：393000米＝3.93×105米．故选：C．
5．下列各组式子中，为同类项的是（　　）
A．﹣3xy与yx B．﹣4x与4x2 C．5x2y与﹣2xy2 D．3a与3b
【解答】解：A．﹣3xy与yx所含字母相同，相同字母的指数也相同，是同类项，故本选项符合题意；
B．﹣4x与4x2含字母相同，相同字母的指数不相同，不是同类项，故本选项不合题意；
C.5x2y与﹣2xy2含字母相同，相同字母的指数不相同，不是同类项，故本选项不合题意；
D.3a与3b含字母不相同，不是同类项，故本选项不合题意．故选：A．
6．如图，下列四个图形是由已知的四个立体图形展开得到的，则对应的标号是（　　）

A．①②③④ B．②①③④ C．③②①④ D．④②①③
【解答】解：由展开图可知第一个图形是②正方体的展开图，
第2个图形是①圆柱体的展开图，
第3个图形是③三棱柱的展开图，
第4个图形是④四棱锥的展开图，
故选：B．
7．若有理数a，b满足|a＋1|+|b﹣3|＝0，则2a+3b的值为（　　）
A．5 B．6 C．7 D．8
【解答】解：由题意得，a＋1＝0，b﹣3＝0，
解得，a＝﹣1，b＝3，
则2a+3b＝7，
故选：C．
8．下列说法中正确的是（　　）
A．﹣a一定表示负数
B．两个有理数比较大小，绝对值大的反而小
C．如果|a﹣5|＝4，则a必定为9
D．如果|a|＝a，则a必定为正数或零
【解答】解：A．当a＜0，﹣a＞0，得﹣a不一定表示负数，那么A不正确，故A不符合题意．
B．|2|＜|3|，但2＜3，得两个有理数比较大小，绝对值大的数不一定小，那么B不正确，故B不符合题意．
C．根据绝对值的定义，|a﹣5|＝4，得a＝9或1，那么C不正确，故C不符合题意．
D．根据绝对值的非负性，|a|＝a≥0，即a是正数或0，那么D正确，故D符合题意．
故选：D．
9．十位数字是a，个位数字是b的两位数是（　　）
A．ab B．a+10b C．ba D．10a+b
【解答】解：由题意可知：两位数为10a+b，
故选：D．
10．有一个数值转换器，原理如图所示，若开始输入x的值是5，可发现第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是4，依次继续下去，第2022次输出的结果是（　　）

A．1 B．2 C．4 D．8
【解答】解：∵开始输入x的值是5，第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是4，
∴第4次输出的结果是：×4＝2，
∴第5次输出的结果是：×2＝1，
∴第6次输出的结果是：3×1+1＝4，
∴第7次输出的结果是2，
…，
∴从第3次开始，输出的结果每3个一循环，分别是4，2，1，
∵（2022﹣2）÷3＝673…1，
∴第2020次输出的结果是4．
故选：A．
二．填空题（共5小题）
11．比较大小：﹣3.14　＞　﹣π（用“＞”“＜”“＝”连接）．
【解答】解：∵|﹣3.14|＝3.14＜|﹣π|，
∴﹣3.14＞﹣π．
故答案为：＞．
12．已知单项式﹣3x3yn与5xm+4y3是同类项，则m﹣n的值为　﹣4　．
【解答】解：∵单项式﹣3x3yn与5xm+4y3是同类项，
∴m+4＝3，n＝3，
解得m＝﹣1，n＝3，
∴m﹣n＝﹣1﹣3＝﹣4．
故答案为：﹣4．
13．数轴上点A表示﹣2，从A出发，沿数轴移动4个单位长度到达点B，则点B表示的数是　﹣6或2　．
【解答】解：当B点在A的左边，则B表示的数为：﹣2﹣4＝﹣6；
若B点在A的右边，则B表示的数为﹣2+4＝2．
14．已知2x﹣3y﹣5＝0，则6x﹣9y+15＝　30　．
【解答】解：∵2x﹣3y﹣5＝0，
∴2x﹣3y＝5，
又∵6x﹣9y+15＝3（2x﹣3y）+15，
∴6x﹣9y+15＝3×5+15＝30，
故答案为：30．
15．已知a，b，c是三个有理数，它们在数轴上的位置如图所示，化简|a﹣b|+|c﹣a|﹣|b+c|＝　2a　．

【解答】解：由数轴知c＜b＜0＜a，
则a﹣b＞0，c﹣a＜0，b+c＜0，
∴原式＝（a﹣b）﹣（c﹣a）+（b+c）
＝a﹣b﹣c+a+b+c
＝2a．
故答案为：2a．
三．解答题（共7小题）
16．计算与合并同类项：
（1）－23÷×(－)2； （2）(－－)×(－48)；
（3）－22÷(－1)2020－|－7|×5； （4）12－(－18)＋(－7)＋(－12)；
（5）4a2+3b2﹣2ab﹣3a2﹣5b2； （6）2x3﹣6x﹣6x3﹣2+9x+8．
【解答】解：（1）原式＝－8；（2）原式＝10；（3）原式＝－39；（4）原式＝11；（5）原式＝a2﹣2b2﹣2ab；（6）原式＝﹣4x3+3x+6．
17．（1）在数轴上表示下列各数：，﹣2，﹣4，3；

（2）请将上面各数用“＜”号连接起来．
【解答】解：（1）如图：

（2）从小到大排列为：﹣4＜﹣2＜＜3．
18．砀山酥梨是一种驰名中外的特色水果，它是梨的一种，因为出产于砀山县而得名．现有20筐砀山酥梨，以每筐25千克的质量为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克）
﹣3
﹣2
﹣1.5
0
1
2.5
筐数
1
4
2
3
2
8
（1）这20筐砀山酥梨中，最重的一筐比最轻的一筐重多少千克？
（2）与标准质量比较，这20筐砀山酥梨总计超过或不足多少千克？
（3）若砀山酥梨每千克售价4元，则这20筐砀山酥梨可卖多少元？
【解答】解：（1）最重的质量为：25+2.5＝27.5kg，最轻的质量为：25﹣3＝22kg，故最重的一筐比最轻的一筐重：27.5﹣22＝5.5kg；
（2）与标准质量比较，这20筐砀山酥梨总计超出：﹣3×1+（﹣2）×4+（﹣1.5）×2+0×3+1×2+2.5×8＝8kg；
（3）这20筐砀山酥梨价格为：（20×25+8）×4＝2032元
19．如图是一个长为4cm，宽为3cm的长方形纸片
（1）若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是　圆柱　，这能说明的事实是　面动成体　．
（2）求：当此长方形纸片绕长边所在直线旋转一周时（如图1），所形成的几何体的体积．
（3）求：当此长方形纸片绕短边所在直线旋转一周时（如图2），所形成的几何体的体积．

【解答】解：（1）若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是圆柱，这能说明的事实是面动成体；
（2）绕长边旋转得到的圆柱的底面半径为3cm，高为4cm，体积＝π×32×4＝36πcm3；
（3）绕短边旋转得到的圆柱底面半径为4cm，高为3cm，体积＝π×42×3＝48πcm3．
故答案为：圆柱；面动成体．36πcm3；48πcm3．
20．（8分）（1）已知多项式（a﹣2）m2+（2b+1）mn﹣m+n﹣7是关于m，n的多项式，若该多项式不含二次项，则3a+2b＝_______．
（2）如果关于x，y的多项式ax﹣2y+5与多项式4x+by+1的差与x、y的取值无关，求a+b的值．
【解答】解：（1）∵多项式（a﹣2）m2+（2b+1）mn﹣m+n﹣7是关于m，n的多项式，该多项式不含二次项，
∴a﹣2＝0，2b+1＝0，
解得：a＝2，b＝﹣，
∴3a+2b＝3×2+2×（﹣）＝5．
（2）由题意得： ax﹣2y+5﹣（4x+by+1）
＝ax﹣2y+5﹣4x﹣by﹣1
＝（a－4）x﹣（2＋b）y+4
则：2＋b＝0，解得：b＝－2；a－4＝0，解得：a＝4；
∴a+b＝－2＋4＝2．
21．（8分）【阅读材料】问题：如何计算呢？小红带领的数学兴趣小组通过探索完成了这道题的计算．
他们的解法如下：
解：原式＝（1﹣）+（）+（）+…+（）＝1﹣＝．
根据材料，请你完成下列计算：
（1）计算：＋；
（2）直接写出结果：＝　 　；
（3）计算：＋．
【解答】解：（1）原式＝1﹣+﹣+﹣+－+－
＝1﹣
＝；
（2）＝；
故答案为：；
（3）＋
＝×[（1﹣）+（﹣）+…+（﹣）＋（－）]
＝×[1﹣]
＝．
23．如图，已知数轴上原点为O，点B表示的数为﹣2，A在B的右边，且A与B的距离是5，动点P从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，动点Q从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，设运动时间为t（t＞0）秒．

（1）写出数轴上点A表示的数　3　，与点A的距离为3的点表示的数是　0或6　．
（2）点P表示的数　（3t﹣2）　（用含t的代数式表示），点Q表示的数　（﹣4t+3）　（用含t的代数式表示）．
（3）问点P与点Q何时到点O距离相等？
【解答】解：（1）∵点B表示的数为﹣2，A在B的右边，且A与B的距离是5，
∴点A表示的数为﹣2+5＝3．
∵3﹣3＝0，3+3＝6，
∴与点A的距离为3的点表示的数是0或6．
故答案为：3；0或6．
（2）当运动时间为t秒时，点P表示的数为3t﹣2，点Q表示的数为﹣4t+3．
故答案为：（3t﹣2）；（﹣4t+3）．
（3）依题意，得：|3t﹣2|＝|﹣4t+3|，
即3t﹣2＝﹣4t+3或3t﹣2＝4t﹣3，
解得：t＝或t＝1．
答：当t＝或1时，点P与点Q到点O距离相等．