2020-2022年浙江中考数学3年真题汇编 专题07 二次函数（学生卷+教师卷）

这是一份2020-2022年浙江中考数学3年真题汇编 专题07 二次函数（学生卷+教师卷），文件包含专题07二次函数-三年2020-2022中考数学真题分项汇编浙江专用解析版docx、专题07二次函数-三年2020-2022中考数学真题分项汇编浙江专用原卷版docx等2份试卷配套教学资源，其中试卷共55页， 欢迎下载使用。
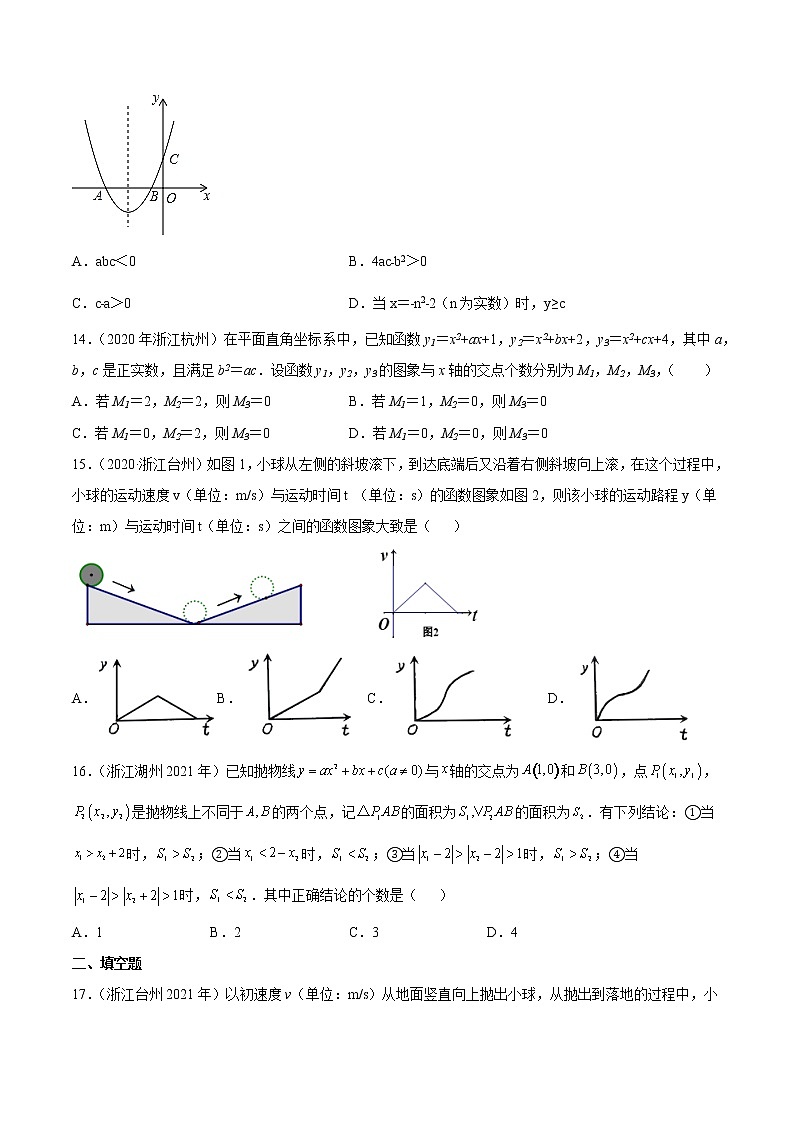
专题07  二次函数 一、单选题(共0分)1．（2022年浙江杭州）已知二次函数（a，b为常数）．命题①：该函数的图像经过点(1，0)；命题②：该函数的图像经过点(3，0)；命题③：该函数的图像与x轴的交点位于y轴的两侧；命题④：该函数的图像的对称轴为直线．如果这四个命题中只有一个命题是假命题，则这个假命题是（       ）A．命题① B．命题② C．命题③ D．命题④2．（2022年浙江宁波）点A（m-1，y1），B（m，y2）都在二次函数y=（x-1）2+n的图象上．若y1＜y2，则m的取值范围为（       ）A． B． C． D．3．（2020年浙江湖州）把抛物线y=x2向上平移3个单位，平移后抛物线的表达式是(       )A．y=-3 B．y=+3 C．y= D．y=4．（2020年浙江温州）已知(﹣3，)，(﹣2，)，(1，)是抛物线上的点，则（       ）A． B． C． D．5．（浙江衢州2020年）二次函数y=x2的图象平移后经过点（2，0），则下列平移方法正确的是（　　）A．向左平移2个单位，向下平移2个单位B．向左平移1个单位，向上平移2个单位C．向右平移1个单位，向下平移1个单位D．向右平移2个单位，向上平移1个单位6．（2022年浙江绍兴）已知抛物线的对称轴为直线，则关于x的方程的根是（       ）A．0，4 B．1，5 C．1，－5 D．－1，57．（2022年浙江温州）已知点都在抛物线上，点A在点B左侧，下列选项正确的是（       ）A．若，则 B．若，则C．若，则 D．若，则8．（2020年浙江杭州）设函数y＝a（x﹣h）2+k（a，h，k是实数，a≠0），当x＝1时，y＝1；当x＝8时，y＝8，（　　）A．若h＝4，则a＜0 B．若h＝5，则a＞0C．若h＝6，则a＜0 D．若h＝7，则a＞09．（2022年浙江舟山）已知点，在直线（k为常数，）上，若的最大值为9，则c的值为（       ）A． B．2 C． D．110．（浙江杭州2021年）在“探索函数的系数，，与图象的关系”活动中，老师给出了直角坐标系中的四个点：，，，，同学们探索了经过这四个点中的三个点的二次函数的图象，发现这些图象对应的函数表达式各不相同，其中的值最大为（       ）A． B． C． D．11．（浙江杭州2021年）已知和均是以为自变量的函数，当时，函数值分别为和，若存在实数，使得，则称函数和具有性质．以下函数和具有性质的是（       ）A．和B．和C．和D．和12．（浙江绍兴2021年）关于二次函数的最大值或最小值，下列说法正确的是（　　）A．有最大值4 B．有最小值4 C．有最大值6 D．有最小值613．（2020年浙江宁波）如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于A，B两点，与y轴正半轴交于点C，它的对称轴为直线x＝﹣1．则下列选项中正确的是（　　）A．abc＜0 B．4ac﹣b2＞0C．c﹣a＞0 D．当x＝﹣n2﹣2（n为实数）时，y≥c14．（2020年浙江杭州）在平面直角坐标系中，已知函数y1＝x2+ax+1，y2＝x2+bx+2，y3＝x2+cx+4，其中a，b，c是正实数，且满足b2＝ac．设函数y1，y2，y3的图象与x轴的交点个数分别为M1，M2，M3，（　　）A．若M1＝2，M2＝2，则M3＝0 B．若M1＝1，M2＝0，则M3＝0C．若M1＝0，M2＝2，则M3＝0 D．若M1＝0，M2＝0，则M3＝015．（2020·浙江台州）如图1，小球从左侧的斜坡滚下，到达底端后又沿着右侧斜坡向上滚，在这个过程中，小球的运动速度v（单位：m/s）与运动时间t （单位：s）的函数图象如图2，则该小球的运动路程y（单位：m）与运动时间t（单位：s）之间的函数图象大致是（       ） A．B．C． D．16．（浙江湖州2021年）已知抛物线与轴的交点为和，点，是抛物线上不同于的两个点，记的面积为的面积为．有下列结论：①当时，；②当时，；③当时，；④当时，．其中正确结论的个数是（       ）A．1 B．2 C．3 D．4二、填空题17．（浙江台州2021年）以初速度v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是h＝vt4.9t2，现将某弹性小球从地面竖直向上抛出，初速度为v1，经过时间t1落回地面，运动过程中小球的最大高度为h1（如图1）；小球落地后，竖直向上弹起，初速度为v2，经过时间t2落回地面，运动过程中小球的最大高度为h2（如图2）．若h1＝2h2，则t1：t2＝_____．18．（浙江湖州2021年）已知在平面直角坐标系中，点的坐标为是抛物线对称轴上的一个动点．小明经探究发现：当的值确定时，抛物线的对称轴上能使为直角三角形的点的个数也随之确定．若抛物线的对称轴上存在3个不同的点，使为直角三角形，则的值是____．三、解答题19．（2022年浙江湖州）如图1，已知在平面直角坐标系xOy中，四边形OABC是边长为3的正方形，其中顶点A，C分别在x轴的正半轴和y轴的正半轴上，抛物线经过A，C两点，与x轴交于另一个点D． (1)①求点A，B，C的坐标；②求b，c的值．(2)若点P是边BC上的一个动点，连结AP，过点P作PM⊥AP，交y轴于点M（如图2所示）．当点P在BC上运动时，点M也随之运动．设BP＝m，CM＝n，试用含m的代数式表示n，并求出n的最大值．20．（浙江湖州2021年）如图，已知经过原点的抛物线与轴交于另一点A(2，0)．（1）求的值和抛物线顶点的坐标；（2）求直线的解析式．          21．（2020年浙江温州）已知抛物线经过点(1，﹣2)，(﹣2，13)．（1）求a，b的值；（2）若(5，)，(m，)是抛物线上不同的两点，且，求m的值．       22．（2022年浙江宁波）为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量y千克与每平方米种植的株数x（，且x为整数）构成一种函数关系．每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克．(1)求y关于x的函数表达式．(2)每平方米种植多少株时，能获得最大的产量？最大产量为多少千克？          23．（浙江宁波2021年中考数学试卷）如图，二次函数（a为常数）的图象的对称轴为直线． （1）求a的值．（2）向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式．    24．（2022年浙江绍兴）已知函数（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．(1)求b，c的值．(2)当﹣4≤x≤0时，求y的最大值．(3)当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．          25．（2022年浙江嘉兴）已知抛物线L1：y＝a(x＋1)2－4（a≠0）经过点A(1，0)．(1)求抛物线L1的函数表达式．(2)将抛物线L1向上平移m（m＞0）个单位得到抛物线L2．若抛物线L2的顶点关于坐标原点O的对称点在抛物线L1上，求m的值．(3)把抛物线L1向右平移n（n＞0）个单位得到抛物线L3，若点B(1，y1)，C(3，y2)在抛物线L3上，且y1＞y2，求n的取值范围．         26．（2020年浙江宁波）如图，在平面直角坐标系中，二次函数y＝ax2+4x﹣3图象的顶点是A，与x轴交于B，C两点，与y轴交于点D．点B的坐标是（1，0）．（1）求A，C两点的坐标，并根据图象直接写出当y＞0时x的取值范围．（2）平移该二次函数的图象，使点D恰好落在点A的位置上，求平移后图象所对应的二次函数的表达式．      27．（2022年浙江金华）“八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：①统计售价与需求量的数据，通过描点（图1），发现该蔬菜需求量（吨）关于售价x（元/千克）的函数图象可以看成抛物线，其表达式为，部分对应值如表：售价x（元/千克）…2.533.54…需求量（吨）…7.757.26.555.8… ②该蔬菜供给量（吨）关于售价x（元/千克）的函数表达式为，函数图象见图1．③1~7月份该蔬菜售价（元/千克），成本（元/千克）关于月份t的函数表达式分别为，，函数图象见图2．请解答下列问题：(1)求a，c的值．(2)根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由．(3)求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．       28．（浙江温州2021年）已知抛物线经过点．（1）求抛物线的函数表达式和顶点坐标．（2）直线交抛物线于点，，为正数．若点在抛物线上且在直线下方（不与点，重合），分别求出点横坐标与纵坐标的取值范围，   29．（浙江衢州2021年）如图1是一座抛物线型拱桥侧面示意图．水面宽AB与桥长CD均为24m，在距离D点6米的E处，测得桥面到桥拱的距离EF为1.5m，以桥拱顶点O为原点，桥面为x轴建立平面直角坐标系．（1）求桥拱项部O离水面的距离．（2）如图2，桥面上方有3根高度均为4m的支柱CG，OH，DI，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为1m．①求出其中一条钢缆抛物线的函数表达式．②为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值．            30．（浙江绍兴2021年）小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体ACB是抛物线的一部分，抛物线的顶点C在y轴上，杯口直径，且点A，B关于y轴对称，杯脚高，杯高，杯底MN在x轴上．（1）求杯体ACB所在抛物线的函数表达式（不必写出x的取值范围）．（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯体所在抛物线形状不变，杯口直径，杯脚高CO不变，杯深与杯高之比为0.6，求的长．      31．（浙江杭州2021年）在直角坐标系中，设函数（，是常数，）．（1）若该函数的图象经过和两点，求函数的表达式，并写出函数图象的顶点坐标．（2）写出一组，的值，使函数的图象与轴有两个不同的交点，并说明理由．（3）已知，当（，是实数，）时，该函数对应的函数值分别为，．若，求证． 32．（浙江金华2021年）某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线第一象限部分的函数表达式为．（1）求雕塑高OA．（2）求落水点C，D之间的距离．（3）若需要在OD上的点E处竖立雕塑EF，，．问：顶部F是否会碰到水柱？请通过计算说明．      33．（2022年浙江杭州）设二次函数（b，c是常数）的图像与x轴交于A，B两点．(1)若A，B两点的坐标分别为(1，0)，(2，0)，求函数的表达式及其图像的对称轴．(2)若函数的表达式可以写成（h是常数）的形式，求的最小值．(3)设一次函数（m是常数）．若函数的表达式还可以写成的形式，当函数的图像经过点时，求的值．     34．（2020年浙江杭州）在平面直角坐标系中，设二次函数y1＝x2+bx+a，y2＝ax2+bx+1（a，b是实数，a≠0）．（1）若函数y1的对称轴为直线x＝3，且函数y1的图象经过点（a，b），求函数y1的表达式．（2）若函数y1的图象经过点（r，0），其中r≠0，求证：函数y2的图象经过点（，0）．（3）设函数y1和函数y2的最小值分别为m和n，若m+n＝0，求m，n的值．        35．（2022·浙江丽水）如图，已知点在二次函数的图像上，且． (1)若二次函数的图像经过点．①求这个二次函数的表达式；②若，求顶点到的距离；(2)当时，二次函数的最大值与最小值的差为1，点M，N在对称轴的异侧，求a的取值范围．