2018-2022年江西中考数学5年真题1年模拟汇编 专题07 几何图形的性质（学生卷+教师卷）

这是一份2018-2022年江西中考数学5年真题1年模拟汇编 专题07 几何图形的性质（学生卷+教师卷），文件包含专题07几何图形的性质-5年2018-2022中考1年模拟数学分项汇编江西专用解析版docx、专题07几何图形的性质-5年2018-2022中考1年模拟数学分项汇编江西专用原卷版docx等2份试卷配套教学资源，其中试卷共129页， 欢迎下载使用。
专题07 几何图形的性质

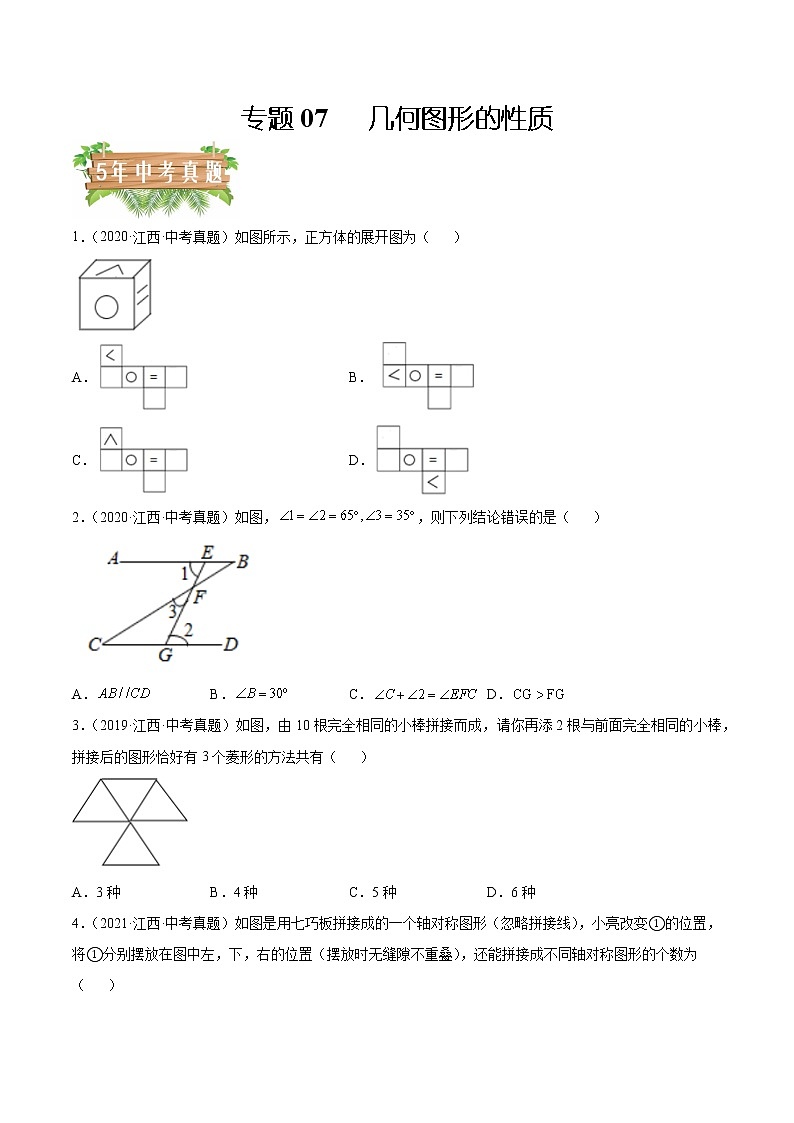
1．（2020·江西·中考真题）如图所示，正方体的展开图为（       ）

A． B．
C． D．
【答案】A
【解析】
【分析】
根据正方体的展开图的性质判断即可；
【详解】
A中展开图正确；
B中对号面和等号面是对面，与题意不符；
C中对号的方向不正确，故不正确；
D中三个符号的方位不相符，故不正确；
故答案选A．
【点睛】
本题主要考查了正方体的展开图考查，准确判断符号方向是解题的关键．
2．（2020·江西·中考真题）如图，，则下列结论错误的是（       ）

A． B． C． D．
【答案】C
【解析】
【分析】
由可对A进行判断；根据三角形外角的性质可对B进行判断；求出∠C，根据大角对大边，小角对小边可对D进行判断；求出可对C进行判断．
【详解】
，
，故选项A正确；
，
，
又，
，故选项B正确；
，
，
，

，故选项D正确；
，
，
而
，故选项C错误．
故选C．
【点睛】
此题主要考查了平行线的判定与性质，三角形外角的性质等知识，熟练掌握性质与判定是解答此题的关键．
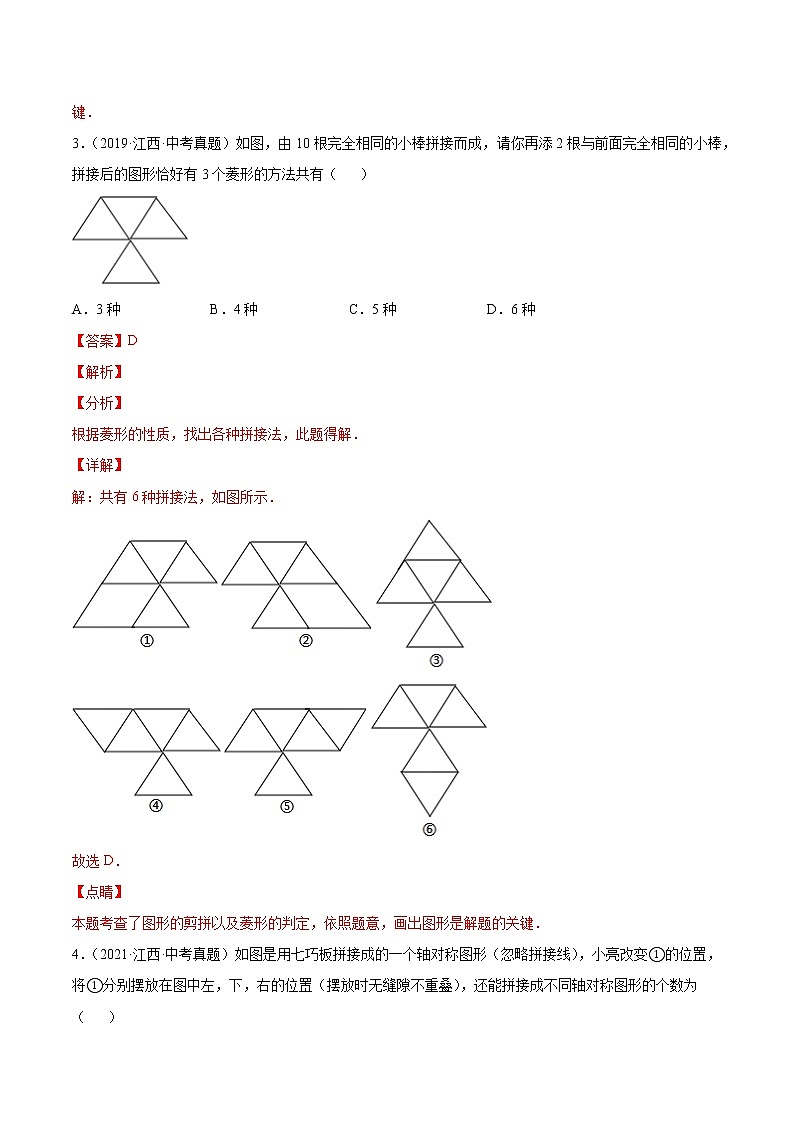
3．（2019·江西·中考真题）如图，由10根完全相同的小棒拼接而成，请你再添2根与前面完全相同的小棒，拼接后的图形恰好有3个菱形的方法共有（       ）

A．3种 B．4种 C．5种 D．6种
【答案】D
【解析】
【分析】
根据菱形的性质，找出各种拼接法，此题得解．
【详解】
解：共有6种拼接法，如图所示．


故选D．
【点睛】
本题考查了图形的剪拼以及菱形的判定，依照题意，画出图形是解题的关键．
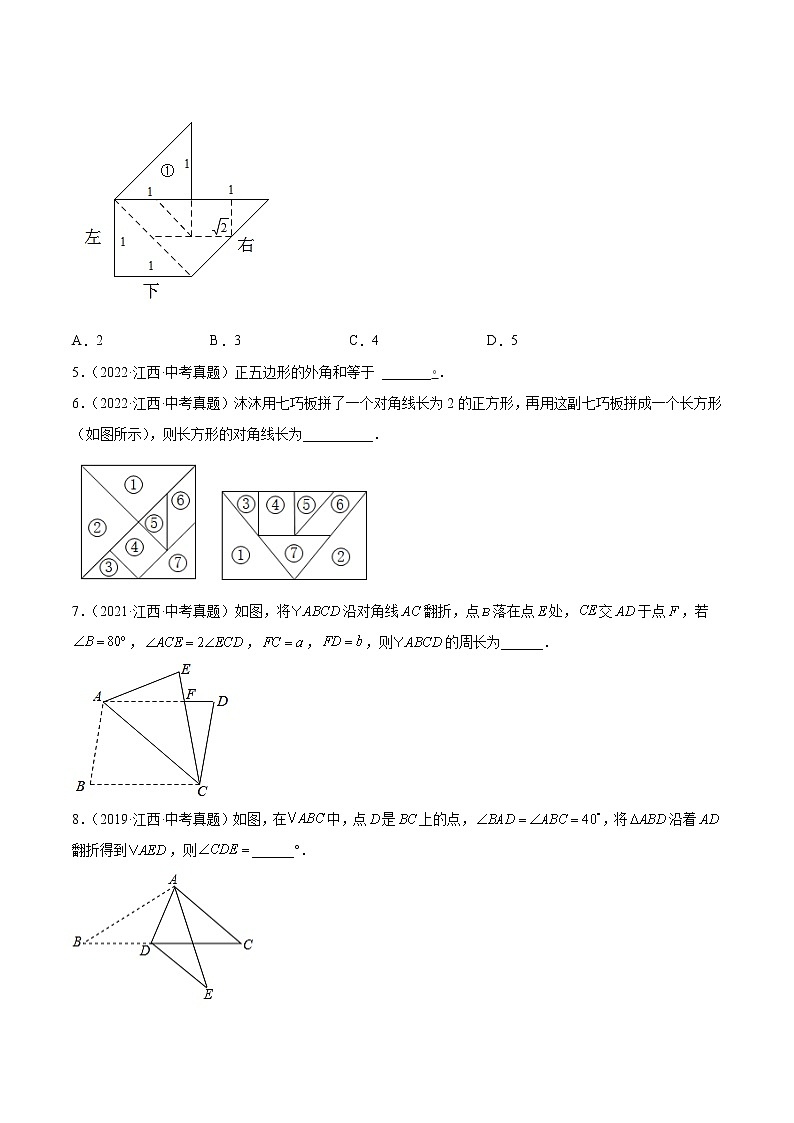
4．（2021·江西·中考真题）如图是用七巧板拼接成的一个轴对称图形（忽略拼接线），小亮改变①的位置，将①分别摆放在图中左，下，右的位置（摆放时无缝隙不重叠），还能拼接成不同轴对称图形的个数为（       ）

A．2 B．3 C．4 D．5
【答案】B
【解析】
【分析】
该题可以自己动手进行拼接，根据勾股定理得知①的直角边为1和1，斜边为，拼接时要依据重合的边要相等，然后根据轴对称图形的概念进行判断即可．
【详解】
在左侧构成轴对称图形如图：

在下方构成轴对称图形如图：

在右侧构成轴对称图形如图:

【点睛】
本题考查勾股定理，图形的拼接以及轴对称图形的判断，掌握轴对称图形的概念是解题的关键．
5．（2022·江西·中考真题）正五边形的外角和等于 _______◦．
【答案】360
【解析】
【详解】
试题分析：任何n边形的外角和都等于360度.
考点：多边形的外角和.
6．（2022·江西·中考真题）沐沐用七巧板拼了一个对角线长为2的正方形，再用这副七巧板拼成一个长方形（如图所示），则长方形的对角线长为__________．

【答案】
【解析】
【分析】
根据图形可得长方形的长是正方形的对角线为2，长方形的宽是正方形对角线的一半为1，然后利用勾股定理即可解决问题．
【详解】
解：根据图形可知：长方形的长是正方形的对角线为2，长方形的宽是正方形对角线的一半为1，
∴根据勾股定理可知，长方形的对角线长：．
故答案为：．
【点睛】
本题主要考查了正方形的性质，七巧板，矩形的性质，勾股定理，解决本题的关键是所拼成的正方形的特点确定长方形的长与宽．
7．（2021·江西·中考真题）如图，将沿对角线翻折，点落在点处，交于点，若，，，，则的周长为______．

【答案】4a+2b
【解析】
【分析】
根据题意并利用折叠的性质可得出∠ACE=∠ACB=2∠ECD，计算可得到∠ECD=20，∠ACE=∠ACB=40，利用三角形的外角性质得到∠CFD=∠D=80，再等角对等边即可求解．
【详解】
解：由折叠的性质可得：∠ACE=∠ACB，
∵∠ACE=2∠ECD，
∴∠ACE=∠ACB=2∠ECD，
∵四边形ABCD是平行四边形，
∴∠FAC=∠FCA，∠B+∠BCD=180，即∠B+∠ACE+∠ACB+∠ECD=180，
∴∠ECD=20，∠ACE=∠ACB=40=∠FAC，
∠CFD=∠FAC+∠FCA=80=∠B=∠D，
∴AF=CF=CD=a，即AD=a+b，
则▱ABCD的周长为2AD+2CD=4a+2b，
故答案为：4a+2b．
【点睛】
本题考查了平行四边形的性质，折叠的性质，等腰三角形的性质，正确的识别图形是解题的关键．
8．（2019·江西·中考真题）如图，在中，点是上的点，，将沿着翻折得到，则______°．

【答案】20
【解析】
【分析】
根据三角形内角和和翻折的性质解答即可．
【详解】
解：，将沿着翻折得到，
，，
，
故答案为20
【点睛】
此题考查翻折的性质，关键是根据三角形内角和和翻折的性质解答．
9．（2020·江西·中考真题）矩形纸片，长，宽，折叠纸片，使折痕经过点，交边于点，点落在点处，展平后得到折痕，同时得到线段，，不再添加其它线段，当图中存在角时，的长为__________厘米．

【答案】或或
【解析】
【分析】
分∠ABE=30°或∠AEB=30°或∠ABA′=30°时三种情况，利用锐角三角函数进行求解即可．
【详解】
解：当∠ABE=30°时，
∵AB=4cm，∠A=90°，
∴AE=AB·tan30°=cm；
当∠AEB=30°时，则∠ABE=60°，
∵AB=4cm，∠A=90°，
∴AE=AB·tan60°=cm；
当∠ABE=15°时，∠ABA′=30°，延长BA′交AD于F，如下图所示，

设AE=x，则EA′=x，，
∵AF=AE+EF=ABtan30°=，
∴，
∴，
∴ cm．
故答案为：或或．
【点睛】
本题考查了矩形与折叠，以及分类讨论的数学思想，分类讨论是解答本题的关键．
10．（2020·江西·中考真题）如图，平分，，的延长线交于点，若，则的度数为__________．

【答案】
【解析】
【分析】
如图，连接，延长与交于点利用等腰三角形的三线合一证明是的垂直平分线，从而得到 再次利用等腰三角形的性质得到：从而可得答案．
【详解】
解：如图，连接，延长与交于点
平分，，

是的垂直平分线，





故答案为：

【点睛】
本题考查的是等腰三角形的性质，掌握等腰三角形的三线合一是解题的关键．
11．（2018·江西·中考真题）如图，在矩形ABCD中，AD=3，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG，点B的对应点E落在CD上，且DE=EF，则AB的长为_____．

【答案】3
【解析】
【详解】
【分析】根据旋转的性质知AB=AE，在直角三角形ADE中根据勾股定理求得AE长即可得.
【详解】∵四边形ABCD是矩形，∴∠D=90°，BC=AD=3，
∵将矩形ABCD绕点A逆时针旋转得到矩形AEFG，
∴EF=BC=3，AE=AB，
∵DE=EF，
∴AD=DE=3，
∴AE==3，
∴AB=3，
故答案为3.
【点睛】本题考查矩形的性质和旋转的性质，熟知旋转前后哪些线段是相等的是解题的关键.
12．（2018·江西·中考真题）在正方形中，=6，连接，，是正方形边上或对角线上一点，若=2，则的长为____________ .
【答案】2或或
【解析】
【分析】
根据题意分情况画出符合题意的图形，然后针对每一个图形利用勾股定理进行求解即可得到答案．
【详解】
解：∵四边形ABCD是正方形，
∴AD=AB=6，∠BAD=90°，∠DAC=45°，
∴AC=BD=6；
如图1，当点P在AD上时，
∵AP+PD=AD=6，PD=2AP，
∴AP=2；

如图2，当点P在AB上时，
∵∠PAD=90°，
∴AP2+AD2=DP2，
∵AD=6，PD=2AP，
∴AP2+36=4AP2，
∴AP=；

如图3，当点P在AC上时，作PN⊥AD于点N，
设AN=x，则有DN=6-x，PN=x，
由勾股定理得AP=x，PD=，
∵PD=2AP，
∴=2x，
∴x=或x=（不符合题意，舍去），
∴AP=x=，

当点P在其余边或对角线上时，不存在可以使PD=2AP的点，
综上，AP的长为2，，，
故答案为2或或．
【点睛】
本题考查了正方形的性质，勾股定理的应用等，难度较大，解题的关键是正确画出符合题意的图形．
13．（2022·江西·中考真题）如图是的正方形网格，请仅用无刻度的直尺按要求完成以下作图（保留作图痕迹）．


(1)在图1中作的角平分线；
(2)在图2中过点作一条直线，使点，到直线的距离相等．
【答案】(1)作图见解析部分
(2)作图见解析部分
【解析】
【分析】
（1）连接，，与交于点，作射线即可；
（2）取格点，过点和点作直线即可．
(1)
解：如图1，连接、，与交于点，设小正方形的边长为1个单位，
∵线段和是矩形的两条对角线且交于点，
∴，
又∵，，
∴，
∴平分，
∴射线即为所作；


(2)
如图2，连接、、、，直线经过点和点，设小正方形的边长为1个单位，
∴，，
，，
∴，
∴四边形是菱形，
又∵，，，
在和中，

∴，
∴，
∵，
∴，
∴，
∴四边形是正方形，
∴，，且，
∴直线即为所作．


【点睛】
本题考查作图一应用与设计作图，考查了等腰三角形三线合一的性质，矩形的性质，正方形的判定和性质，全等三角形的判定和性质，直角三角形两锐角互余，勾股定理等知识．解题的关键是理解题意，学会利用数形结合的思想解决问题．
14．（2022·江西·中考真题）图1是某长征主题公园的雕塑，将其抽象成如图2所示的示意图，已知，A，D，H，G四点在同一直线上，测得．（结果保留小数点后一位）


(1)求证：四边形为平行四边形；
(2)求雕塑的高（即点G到的距离）．
（参考数据：）
【答案】(1)见解析
(2)雕塑的高为7.5m，详见解析
【解析】
【分析】
（1）根据平行四边形的定义可得结论；
（2）过点G作GP⊥AB于P，计算AG的长，利用 ∠A的正弦可得结论．
(1)
证明：∵，
∴∠CDG＝∠A，
∵∠FEC＝∠A，
∴ ∠FEC＝∠CDG，
∴EF∥DG，
∵FG∥CD，
∴四边形DEFG为平行四边形；
(2)
如图，过点G作GP⊥AB于P，
∵四边形DEFG为平行四边形，
∴DG＝EF＝6.2，
∵AD＝1.6，
∴AG＝DG+AD＝6.2+1.6＝7.8，
在Rt△APG中，sinA= ，
∴=0.96，
∴PG=7.8×0.96＝7.488≈7.5．
答：雕塑的高为7.5m.

【点睛】
本题考查解直角三角形的应用，解题的关键是理解题意，正确作辅助线构建直角三角形解决问题．
15．（2022·江西·中考真题）如图，四边形为菱形，点E在的延长线上，．

(1)求证：；
(2)当时，求的长．
【答案】(1)见解析
(2)AE=9
【解析】
【分析】
（1）根据四边形ABCD是菱形，得出，，根据平行线的性质和等边对等角，结合，得出，即可证明结论；
（2）根据，得出，代入数据进行计算，即可得出AE的值．
(1)
证明：∵四边形ABCD为菱形，
∴，，
，，
∵，
∴，
∴．
(2)
∵，
∴，
即，
解得：．
【点睛】
本题主要考查了菱形的性质，平行线的性质，等腰三角形的性质，三角形相似的判定和性质，根据题意得出，是解题关键．
16．（2022·江西·中考真题）（1）课本再现：在中，是所对的圆心角，是所对的圆周角，我们在数学课上探索两者之间的关系时，要根据圆心O与的位置关系进行分类．图1是其中一种情况，请你在图2和图3中画出其它两种情况的图形，并从三种位置关系中任选一种情况证明；
（2）知识应用：如图4，若的半径为2，分别与相切于点A，B，，求的长．

【答案】（1）见解析；（2）
【解析】
【分析】
（1）①如图2，当点O在∠ACB的内部，作直径，根据三角形外角的性质和等腰三角形的性质可得结论；②如图3，当O在∠ACB的外部时，作直径CD，同理可理结论；
（2）如图4，先根据（1）中的结论可得∠AOB=120°，由切线的性质可得∠OAP=∠OBP=90°，可得∠OPA=30°，从而得PA的长．
【详解】
解：（1）①如图2，连接CO，并延长CO交⊙O于点D，

∵OA=OC=OB，
∴∠A=∠ACO，∠B=∠BCO，
∵∠AOD=∠A+∠ACO=2∠ACO，∠BOD=∠B+∠BCO=2∠BCO，
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB，
∴∠ACB=∠AOB；
如图3，连接CO，并延长CO交⊙O于点D，

∵OA=OC=OB，
∴∠A=∠ACO，∠B=∠BCO，
∵∠AOD=∠A+∠ACO=2∠ACO，∠BOD=∠B+∠BCO=2∠BCO，
∴∠AOB=∠AOD-∠BOD=2∠ACO-2∠BCO=2∠ACB，
∴∠ACB=∠AOB；
（2）如图4，连接OA，OB，OP，

∵∠C=60°，
∴∠AOB=2∠C=120°，
∵PA，PB分别与⊙O相切于点A，B，
∴∠OAP=∠OBP=90°，∠APO=∠BPO=∠APB=（180°-120°）=30°，
∵OA=2，
∴OP=2OA=4，
∴PA=
【点睛】
本题考查了切线长定理，圆周角定理等知识，掌握证明圆周角定理的方法是解本题的关键．
17．（2021·江西·中考真题）如图1，四边形内接于，为直径，过点作于点，连接．


（1）求证：；
（2）若是的切线，，连接，如图2．
①请判断四边形ABCO的形状，并说明理由；
②当AB=2时，求AD， AC与围成阴影部分的面积．
【答案】（1）见解析；（2）四边形ABCO是菱形，理由见解析；（3）阴影部分的面积为．
【解析】
【分析】
（1）利用圆内接四边形的性质证得∠D=∠EBC，再利用圆周角的性质证得∠D+∠CAD=，即可证明∠CAD=∠ECB；
（2）①利用切线的性质得到OC⊥EC，从而证明OC∥AE，再证明∠BAO=∠EBC =60°，推出BC∥AO，即可证明四边形ABCO是菱形；②先计算，再利用扇形的面积公式计算，即可求得阴影部分的面积．
【详解】
（1）证明：∵四边形ABCD内接于⊙O，
∴∠D+∠ABC=，
∵∠EBC+∠ABC=，
∴∠D=∠EBC，
∵AD为⊙O直径，
∴∠ACD=，
∴∠D+∠CAD=，
∵CE⊥AB，
∴∠ECB+∠EBC=，
∴∠CAD=∠ECB；
（2）①四边形ABCO是菱形，理由如下：
∵CE是⊙O的切线，
∴OC⊥EC，
∵AB⊥EC，
∴∠OCE=∠E=，
∴∠OCE+∠E=18，
∴OC∥AE，
∴∠ACO=∠BAC，
∵OA=OC，
∴∠ACO=∠CAD，
∴∠BAC=∠CAD，
∵∠CAD=∠ECB，∠CAD=30°，
∴∠EBC=90°-30°=60°，
∴∠BAO=∠EBC =60°，
∴BC∥AO，
∴四边形ABCO是平行四边形，
∵OA=OC，
∴四边形ABCO是菱形；
②∵四边形ABCO是菱形，
∴AO=AB=2，AD=4，
∵∠CAD=30°，
∴CD=AD=2，AC=2，
过点C作CF⊥AD于点F，

∴CF=，
∴，
∵OC∥AE，
∴∠DOC=∠BAO=60°，
∴，
∴阴影部分的面积为．
【点睛】
本题主要考查了切线的性质、菱形的判定和性质以及扇形面积的求法，熟练掌握切线的性质定理以及扇形面积的求法是解答此题的关键．
18．（2021·江西·中考真题）已知正方形的边长为4个单位长度，点是的中点，请仅用无刻度直尺按下列要求作图（保留作图痕迹）．

（1）在图1中，将直线绕着正方形的中心顺时针旋转；
（2）在图2中，将直线向上平移1个单位长度．
【答案】（1）见解析；（2）见解析
【解析】
【分析】
（1）连接BD与AC相交于O，连接AE与BD相交于P，连接CP并延长交AD于F，直线OF即为所求；
（2）设AE与OF交于G，连接OE交CF于H，则直线GH即为所求．
【详解】
（1）如图，直线OF即为所求；

∵AD=CD，∠ADP=∠CDP=45°，DP=DP，
∴△ADP△CDP，
∴∠DAE=∠DCF，
∵AD=CD，∠ADE=∠CDF=90°，
∴△ADE△CDF，
∴DE=DF，
∵点E是CD的中点，
∴点F是AD的中点，
∵∠AOD=90°，且AO=OD，
∴∠AOF=45°；
（1）如图，直线GH即为所求；

由三角形中位线定理知OG=CF=1，OH=AF=1，且∠GOH=90°，
∴OG=OH，
∴△GOH是等腰直角三角形，
∴∠HOC=∠OHG=45°，
∴GH∥AC，且OG =1．
【点睛】
本题考查了正方形的性质，等腰三角形的判定和性质，全等三角形的判定和性质，三角形中位线定理，解题的关键是灵活运用所学知识解决问题．
19．（2019·江西·中考真题）如图1，为半圆的直径，点为圆心，为半圆的切线，过半圆上的点作交于点，连接．
（1）连接，若，求证：是半圆的切线；
（2）如图2，当线段与半圆交于点时，连接，，判断和的数量关系，并证明你的结论．

【答案】（1）见解析；（2）
【解析】
【分析】
（1）连接，根据切线的性质得到，推出四边形是平行四边形，得到，等量代换得到，推出四边形是平行四边形，根据平行四边形的性质得到，于是得到结论；
（2）如图2，连接，根据圆周角定理得到，求得，证得，等量代换即可得到结论．
【详解】
（1）证明：连接，

为半圆的切线，为半圆的直径，
，
，，
四边形是平行四边形，
，
，
，
四边形是平行四边形，
，
，
，
，
，
是半圆的切线；
（2）解：，
理由：如图2，连接，

为半圆的直径，
，
，
，
，
，
，
，
．
【点睛】
本题考查了切线的判定和性质，圆周角定理，平行四边形的判定和性质，正确的作出辅助线是解题的关键．
20．（2018·江西·中考真题）如图，在中，为上一点，以为圆心，长为半径作圆，与相切于点，过点作交的延长线于点,且.
     （1）求证：为的切线；
     （2）若， ,求的长.

【答案】(1)证明见解析；（2）
【解析】
【详解】
【分析】（1）作OE⊥AB于点E，证明△OBC≌△OBE，根据全等三角形的对应边相等可得OE=OC， OE是⊙O的半径 ，OE⊥AB ，即可判定AB为⊙O的切线；   
（2）根据题意先求出AO、BO的长，再证明△AOD∽△BOC，根据相似三角形对应边成比例即可求出AD的长.
【详解】（1）作OE⊥AB于点E，
∵切BC于点C，
∴OC⊥BC，∠ACB=90°，
∵ AD⊥BD，∴∠D=90°，
∴∠ABD＋∠BAD =90°，∠CBD＋∠BOC=90°，
∵∠BOC=∠AOD，∠AOD=∠BAD，
∴∠BOC=∠BAD，
∴∠ABD=∠CBD
在△OBC和△OBE中，
∴△OBC≌△OBE，
∴OE=OC，∴OE是⊙O的半径 ，
∵OE⊥AB ，∴AB为⊙O的切线；   

（2） ∵tan∠ABC=，BC=6，
∴AC=8，∴AB= ，
∵BE=BC=6，∴AE=4，
∵∠AOE=∠ABC，∴tan∠AOE= ，∴EO=3，
∴AO=5，OC=3，∴BO=，
在△AOD和△BOC中，
∴△AOD∽△BOC，∴ ，
即 ，∴AD= .
【点睛】本题考查了切线的判定与性质，相似三角形的判定与性质等，熟练掌握相关的判定与性质定理是解题的关键.
21．（2018·江西·中考真题）如图，在四边形中，∥,=2,为的中点，请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
     （1）在图1中，画出△ABD的BD边上的中线；
     （2）在图2中，若BA=BD, 画出△ABD的AD边上的高 .

【答案】(1)作图见解析；（2）作图见解析.
【解析】
【分析】
（1）根据AB=2CD，AB=BE，可知BE＝CD，再根据BE//CD，可知连接CE，CE与BD的交点F即为BD的中点，连接AF，则AF即为△ABD的BD边上的中线；
（2）由（1）可知连接CE与BD交于点F，则F为BD的中点，根据三角形中位线定理可得EF//AD，EF=AD，则可得四边形ADFE要等腰梯形，连接AF，DE交于点O，根据等腰梯形的性质可推导得出OA=OD，再结合BA=BD可知直线BO是线段AD的垂直平分线，据此即可作出可得△ABD的AD边上的高 .
【详解】
（1）如图AF是△ABD的BD边上的中线；

（2）如图AH是△ABD的AD边上的高.

【点睛】
本题考查了利用无刻度的直尺按要求作图，结合题意认真分析图形的成因是解题的关键.
22．（2020·江西·中考真题）某数学课外活动小组在学习了勾股定理之后，针对图1中所示的“由直角三角形三边向外侧作多边形，它们的面积，，之间的关系问题”进行了以下探究：

类比探究
（1）如图2，在中，为斜边，分别以为斜边向外侧作，，，若，则面积，，之间的关系式为 ；
推广验证
（2）如图3，在中，为斜边，分别以为边向外侧作任意，，，满足，，则（1）中所得关系式是否仍然成立？若成立，请证明你的结论；若不成立，请说明理由；
拓展应用
（3）如图4，在五边形中，，，，，点在上，，，求五边形的面积．
【答案】（1）；（2）结论成立，证明看解析；（3）
【解析】
【分析】
（1）由题目已知△ABD、△ACE、△BCF、△ABC均为直角三角形，又因为，则有∽∽，利用相似三角形的面积比为边长平方的比，列出等式，找到从而找到面积之间的关系；
（2）在△ABD、△ACE、△BCF中，，，可以得到∽∽，利用相似三角形的面积比为边长平方的比，列出等式，从而找到面积之间的关系；
（3）将不规则四边形借助辅助线转换为熟悉的三角形，过点A作AHBP于点H，连接PD，BD，由此可知，，即可计算出，根据△ABP∽△EDP∽△CBD，从而有，由（2）结论有，最后即可计算出四边形ABCD的面积．
【详解】
（1）∵△ABC是直角三角形，
∴，
∵△ABD、△ACE、△BCF均为直角三角形，且，
∴∽∽，
∴，，
∴
∴得证．
（2）成立，理由如下：
∵△ABC是直角三角形，
∴，
∵在△ABD、△ACE、△BCF中，，，
∴∽∽，
∴，，
∴
∴得证．
（3）过点A作AHBP于点H，连接PD，BD，
∵，，
∴，，
∵，
∴，
∴PH=AH=，
∴，，
∴，
∵，ED=2，
∴，，
∴，
∵，
∴△ABP∽△EDP，
∴，，
∴，，
∴，
，
∵，
∴
∵，
∴
∵
∴△ABP∽△EDP∽△CBD
∴
故最后答案为．

【点睛】
（1）（2）主要考查了相似三角形的性质，若两三角形相似，则有面积的比值为边长的平方，根据此性质找到面积与边长的关系即可；（3）主要考查了不规则四边形面积的计算以及（2）的结论，其中合理正确利用前面得出的结论是解题的关键．
23．（2020·江西·中考真题）已知的两边分别与圆相切于点，，圆的半径为．
（1）如图1，点在点，之间的优弧上，，求的度数；
（2）如图2，点在圆上运动，当最大时，要使四边形为菱形，的度数应为多少？请说明理由；
（3）若交圆于点，求第（2）问中对应的阴影部分的周长（用含的式子表示）．

【答案】（1）50°；（2）当∠APB=60°时，四边形APBC为菱形，理由见解析；（3）．
【解析】
【分析】
（1）连接OA、OB，根据切线的性质和多边形内角和定理可得∠AOB+∠APB=180°，然后结合已知求得∠AOB，最后根据圆周角定理即可解答；
（2）连接OA、OB，先观察发现当∠APB=60°时，四边形APBC可能为菱形；然后利用∠APB=60°结合（1）的解答过程可得∠ACB=∠APB=60°，再根据点C运动到PC距离最大，即PC经过圆心；再说明四边形APBC为轴对称图形结合已知条件得到PA =PB=CA =CB，即可得到四边形APBC为菱形；
（3）由于⊙O的半径为r，则OA=r、OP=2 r，再根据勾股定理可得AP=r、PD=r，然后根据弧长公式求得的弧长，最后根据周长公式计算即可．
【详解】
解：（1）如图1，连接OA、OB
∵PA，PB为⊙O的切线
∴∠PAO=∠PBO=90°
∴∠AOB+∠MPN=180°
∵∠MPN=80°
∴∠AOB=180°-∠MPN=100°
∴∠AOB=100°=∠ACB=50°；

（2）当∠APB=60°时，四边形APBC为菱形，理由如下：
如图2：连接OA、OB
由（1）可知∠AOB+∠APB=180°
∵∠APB=60°
∴∠AOB=120°
∴∠ACB=60°=∠APB
∵点C运动到PC距离最大
∴PC经过圆心
∵PA、PB为⊙O的切线
∴四边形APBC为轴对称图形
∵PA=PB，CA=CB，PC平分∠APB和∠ACB.
∴∠APB=∠ACB=60°
∴∠APO=∠BPO=∠ACP=∠BCP=30°
∴PA =PB=CA =CB
∴四边形APBC为菱形；

（3）∵⊙O的半径为r
∴OA=r，OP=2 r
∴AP=r，PD=r
∵∠AOP=60°
∴
∴C阴影．
【点睛】
本题考查了圆的切线的性质、圆周角定理、菱形的判定、弧长公式以及有关圆的最值问题，考查知识点较多，灵活应用所学知识是解答本题的关键．
24．（2019·江西·中考真题）在中，，点在以为直径的半圆内．请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹）．
（1）在图1中作弦，使；

（2）在图2中以为边作一个45°的圆周角．

【答案】（1）见解析；（2）见解析
【解析】
【分析】
（1）分别延长、交半圆于、，利用圆周角定理可等腰三角形的性质可得到，则可判断；
（2）在（1）基础上分别延长、，它们相交于，则连接交半圆于，然后证明，从而根据圆周角定理可判断．
【详解】
解：（1）如下图：分别延长、交半圆于、，线段为所求弦．

理由如下：∵AB=BC,
∴∠B=∠C，
又∵，
∴∠F=∠C，
∴∠C=∠F，
∴EF∥BC，
（2）如下图，（以下画法供参考）：在（1）基础上分别延长、，它们相交于，则连接交半圆于， 则为所作．
理由如下：∵EF∥BC，
∴，
∴∠EBC=∠FCB，
∴MC=MB，
又∵AB=AC，
∴MA垂直平分BC，
∴D为的中点，
∵为半圆，
∴∠CBD=45°.
【点睛】
本题考查了作图复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了圆周角定理．
25．（2019·江西·中考真题）在图1，2，3中，已知，，点为线段上的动点，连接，以为边向上作菱形，且．

（1）如图1，当点与点重合时，________°；
（2）如图2，连接．
①填空：_________（填“>”，“