
所属成套资源:2022——2023学年全国部分地区学校八年级上册期中测试卷(含答案解析)
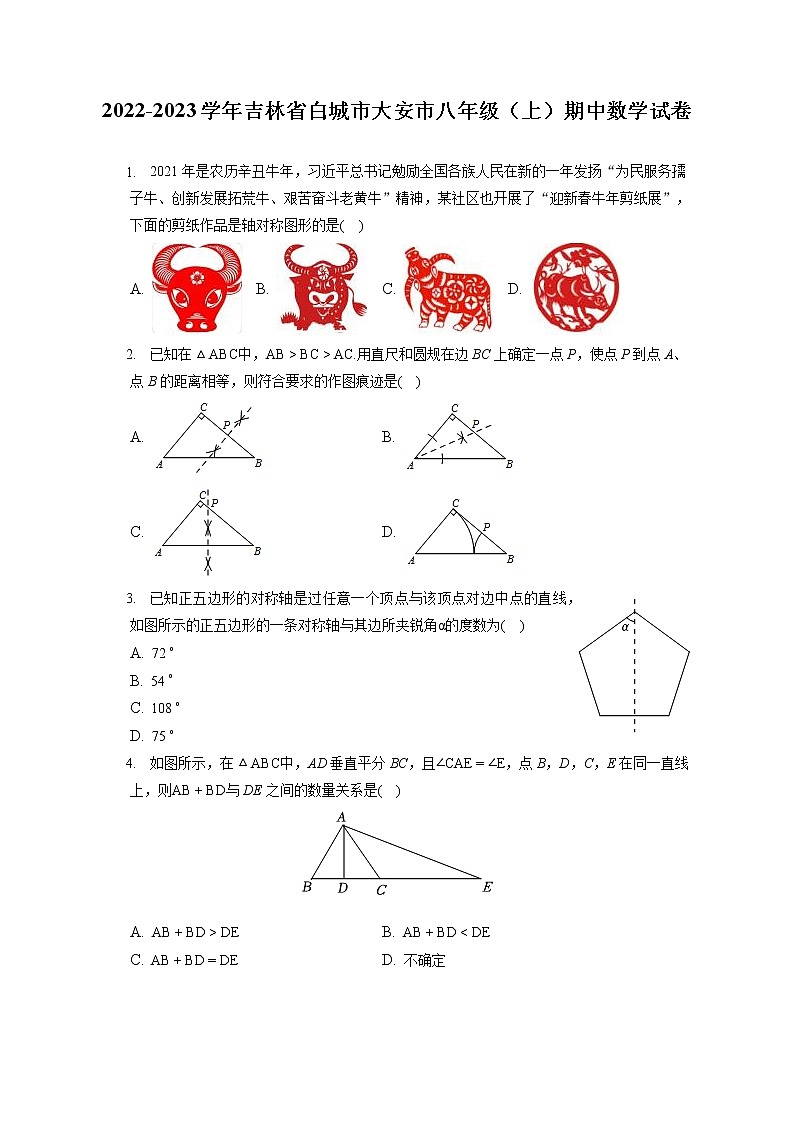
2022-2023学年吉林省白城市大安市八年级(上)期中数学试卷(含答案解析)
展开
这是一份2022-2023学年吉林省白城市大安市八年级(上)期中数学试卷(含答案解析),共20页。试卷主要包含了【答案】C,【答案】B,【答案】1
C. D. 已知正五边形的对称轴是过任意一个顶点与该顶点对边中点的直线,如图所示的正五边形的一条对称轴与其边所夹锐角的度数为( )A.
B.
C.
D. 如图所示,在中,AD垂直平分BC,且,点B,D,C,E在同一直线上,则与DE之间的数量关系是( )
A. B.
C. D. 不确定 如图,在中,,垂足分别为D、E,AD、CE交于点H,已知,,则CH的长是( )
A. 1 B. 2 C. 3 D. 4 如图,在中,,,AD平分交BC于点D,在AB上截取,则的周长为( )A. 9
B. 8
C. 7
D. 6 若a、b、c为三角形的三边,且a,b满足,则第三边c的取值范围是______ . 如图,在中,,D是BC上一点,,,则点D到AB的距离为______ .
如图,中,,CD是高,,,则______
停在湖边的一辆小轿车,如图为车牌号在湖面中的倒影,则这辆小轿车的车牌号码是______.如图,在平面直角坐标系中,点,,则点B的坐标为______.
如图,C为线段AE上一动点不与点A、E重合,在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接下列五个结论:①;②;③;④;⑤其中恒成立的有______填序号
如图,已知,,,,则的度数为______
如图,在中,,,过点B作,交AC于点D,若,则CD的长度为__________.
已知点,,若点A、B关于y轴对称,求的值.如图,在中,,,AD是BC边上的高,AE平分
求的度数;
求的度数.
如图,已知,求证:≌
如图,中,,,DE垂直平分AC,求
图①、图②均是的正方形网格,小正方形的顶点称为格点,的顶点均在格点上请在图①、图②中各画一个三角形同时满足以下两个条件:
以点A为一个顶点,另外两个顶点均在格点上;
与全等,且不与重合.
如图,是等边三角形,分别延长AB,BC,CA到点D,E,F,使,连接DE,EF,FD,判断是什么特殊三角形,并说明理由.
如图,在平面直角坐标系中,的三个顶点坐标分别为,,
画出关于y轴对称的;
如果点在线段AB上,直接写出经过的变换后,点D对应点的坐标.
请计算出的面积.
如图,,点E、N在AB上,点F在CD上,的平分线FM交AB于点G,且,若,求的度数.
如图,在中,,,延长CA至点D,延长CB至点E,使,连接AE,BD,交点为
求证:;
连接OC,若,则的度数是______ 度.
如图①,等边中,AD是BC边上的中线,E为AD上一点点E不与点A重合,以CE为一边在CE下方作等边,连接
猜想线段AE、BF的数量关系:______ 不要求证明;
如图②,当点E为AD延长线上一点时,其他条件不变,中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
如图在和中,,,,连接CD,交AE于点
求证:;
当,时,如图2,延长DC,AB交于点G,求证:是等腰三角形;
在的条件下,是否还存在除,和以外的等腰三角形,如果存在,试将它们全都写出来.
如图,在中,,,,,P、Q是边上的两个动点,其中点P从点A开始沿方向运动,且速度为每秒1cm,点Q从点B开始沿方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
当点Q在边BC上运动时,出发几秒后,是等腰三角形?
当点Q在边CA上运动时,出发几秒后,是以BC或BQ为底边的等腰三角形?
答案和解析 1.【答案】A 【解析】解:选项A能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B、C、D均不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:
根据轴对称图形的概念求解.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】C 【解析】解:要使点P到点A、点B的距离相等,则作AB的垂直平分线.
故选:
根据线段垂直平分线的性质,作AB的垂直平分线,然后利用基本作图对各选项进行判断.
本题考查了作图-基本作图:熟练掌握基本作图作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线也考查了线段垂直平分线的性质.
3.【答案】B 【解析】解:五边形的内角为,,
,
故选:
根据正五边形的性质与轴对称的性质,列式求解即可.
本题考查了轴对称的性质,根据正五边形的性质得到正五边形的内角度数是解题的关键.
4.【答案】C 【解析】解:垂直平分BC,
,,
,
,
,
故选:
根据线段垂直平分线的性质可得,,然后可得,利用等量代换可得
此题主要考查了线段垂直平分线的性质,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
5.【答案】A 【解析】【分析】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA,AAS、HL,要熟练掌握并灵活应用这些方法.
本题可先根据AAS判定≌,可得出,从而得出
【解答】
解:在中,,,
;
,,
对顶角相等,
等量代换;
在和中
,
≌;
;
,,
故选 6.【答案】B 【解析】解:平分,
在和中,
,
≌,
,
,
的周长
故选:
利用已知条件证明≌,得到,从而,根据线段的和差求出,即可求得的周长.
本题考查了全等三角形的性质与判定,解决本题的关键是证明≌
7.【答案】 【解析】解:由题意得,,,
解得,,
,,
故答案为:
根据非负数的性质列式求出a、b,再根据三角形的任意两边之和大于第三边,两边之差小于第三边求解即可.
本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0;三角形的三边关系.
8.【答案】3 【解析】解:过D作于E,
,
平分,
,
,
到AB的距离为
故答案为
由,求得,根据角平分线的性质可知D点到AB的距离等于D点到AC的距离CD长度即可求得结果.
本题主要考查了角平分线的性质,题目简单易懂,观察出D点到AB的距离等于D点到AC的距离CD长度是解题的关键.
9.【答案】15 【解析】解中,,,
,
是高,
,
,
,
,
在中,,,
,
,
故答案是:
求出,根据含角的直角三角形的性质求出,求出,即可得出答案.
本题考查了含30度角的直角三角形,解此题的关键是得出和,难度适中.
10.【答案】wj9458 【解析】解:根据题意,这辆小轿车的车牌号码是
故答案为:
根据镜面对称的性质分析即可.
本题考查了镜面对称,镜面实质上是无数对对应点的对称,连接对应点的线段与镜面垂直并且被镜面平分,即镜面上有每一对对应点的对称轴.
11.【答案】 【解析】解:如图,过点B作轴于点C,则,
,
,
,
,
,
,,
,
,
故答案为:
如图,过点B作轴于点C,通过解直角求出OB的长度;然后再通过解等腰直角来求BC、OC的长度,即点B的坐标.
本题考查了等腰直角三角形、坐标与图形性质.作辅助线构造出直角三角形是解题的关键.
12.【答案】①②③⑤ 【解析】解:①是等边三角形,
,,
是等边三角形,
,,
,
,
在和中,
,
≌,
,故①正确;
③≌,
,
,
在与中,
,
≌,
,故③正确;
②≌,
,
是等边三角形,
,
,
,故②正确;
④,,
,
即
,,
,
,
,故④错误;
⑤,,
,故⑤正确.
综上所述,正确的结论有:①②③⑤.
故答案为:①②③⑤.
①由于和是等边三角形,可知,,,从而证明≌,可推出,故①正确;
③由≌得,结合,,得到≌,由全等三角形的性质可得;故③正确;
②根据≌,以及可推出为等边三角形,又由,根据:内错角相等,两直线平行,可判断②正确;
④根据,,可知,进而可判断④的不正确;
⑤根据三角形内角和定理字形可判断⑤正确.
本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,证明≌是解题的关键.
13.【答案】150 【解析】解:,,,
,
,
,,,
,
故答案为
根据三角形的内角和定理可求解的度数,利用对顶角的性质可得的度数,再利用多边形的内角和定理可计算求解.
本题主要考查多边形的内角和定理,三角形的内角和定理,掌握相关定理是解题的关键.
14.【答案】2 【解析】【分析】
本题考查了等腰三角形与含30度角直角三角形的性质,正确理解在直角三角形中,掌握角所对的直角边等于斜边的一半是解题的关键.
由,推出,所以,由,,推出,所以,,在中,由角所对的直角边等于斜边的一半即可得CD的长.
【解答】
解:因为,
所以,
所以,
因为,,
所以,
所以,
所以,
在中,
因为,
所以
故答案为 15.【答案】解:点,关于y轴对称,
,
解得
故 【解析】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”列方程组求出a、b的值,然后相加计算即可得解.
本题考查了关于原点对称的点的坐标,关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
16.【答案】解:,,,
,
平分,
;
是BC边上的高,
,
,
,
【解析】根据三角形的内角和定理可求解的度数,利用角平分线的定义可求解的度数;
由直角三角形的性质可求解的度数,利用可求解.
本题主要考查三角形内角和定理,三角形的角平分线,高线,掌握三角形的高线,角平分线的定义是解题的关键.
17.【答案】证明:,
在和中
【解析】根据直角三角形全等的判定定理解答.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
18.【答案】解:,
根据线段垂直平分线的性质可推出
【解析】首先利用线段垂直平分线的性质推出,根据等腰三角形的性质可求出,易求的度数.
本题主要考查了线段垂直平分线的性质以及等腰三角形的性质,利用线段垂直平分线的性质是解答此题的关键.
19.【答案】解:如图所示:即为所求;
如图所示:即为所求. 【解析】直接利用网格结合全等三角形的判定方法分析得出答案;
直接利用网格结合全等三角形的判定方法分析得出答案.
此题主要考查了应用设计与作图,正确借助网格分析是解题关键.
20.【答案】解:是等边三角形.理由如下:
是等边三角形,
,,
,
,
,
在和中,
,
≌,
,
同理,≌,
,
,
是等边三角形. 【解析】根据等边三角形的性质得出,,进而推出,,利用SAS证明≌,≌,根据全等三角形的性质及等边三角形的判定即可得解.
此题考查了全等三角形的判定与性质、等边三角形的判定与性质,熟记全等三角形的判定与性质定理是解题的关键.
21.【答案】解:如图,即为所求;
,与D关于y轴对称,
;
【解析】利用轴对称变换的性质分别作出A,B,C的对应点,,即可;
利用轴对称的性质求解即可;
把三角形的面积看成矩形的面积减去周围三个三角形面积即可.
本题考查作图-轴对称变换,三角形的面积等知识,解题的关键是掌握轴对称的性质,属于中考常考题型.
22.【答案】解:,
,
平分,
,
,
,
,
【解析】求出,根据角平分线定义求出,根据平行线的性质求出,根据等腰三角形的性质和三角形内角和定理求出即可.
本题考查了平行线的性质、等腰三角形的性质、三角形内角和定理、角平分线定义等知识点,能根据知识点求出的度数是解此题的关键.
23.【答案】 【解析】证明:,,
在与中,
,
≌,
,
;
由得:,
在与中,
,
≌,
,
,,
,
,
在中,
故答案为
根据全等三角形的判定和性质得出≌,进而得出;
根据全等三角形的判定和性质以及三角形内角和解答.
此题考查全等三角形的判定和性质,关键是根据全等三角形的判定和性质解答.
24.【答案】 【解析】解:,理由如下:
是等边三角形,是等边三角形,
,,,
,
即,
在与中,
,
≌,
;
,理由如下:
是等边三角形,是等边三角形,
,,,
,
即,
在与中,
,
≌,
故答案为:
根据等边三角形的性质和全等三角形的判定和性质解答即可;
根据等边三角形的性质和全等三角形的判定和性质解答即可.
本题考查了等边三角形的性质、全等三角形的判定及其性质等知识.利用相等的角进行等效转是解答本题的关键.
25.【答案】证明:,
,
,
在和中,
,
≌,
,
,,,,
,
,
;
由知,
,
,
,
是等腰三角形;
存在,、、都是等腰三角形. 【解析】证明≌,则,进而可证;
,易求出,由,根据等腰三角形性质,可求出,进而可证是等腰三角形;
由可分别求出,,,进而可得、、都是等腰三角形.
本题考查了等腰三角形的性质等知识点,证明三角形的全等是解本题的关键,此类试题可看成是顶角相等的等腰三角形手拉手模型,解题时注意图形的变化,综合性较强,难度较大.
26.【答案】解:由题意可知,,
,
,
当为等腰三角形时,则有,
即,解得,
出发秒后能形成等腰三角形;
①当是以BC为底边的等腰三角形时:,如图1所示,
则,
,
,
,
,
秒,
秒,
秒
②当,是以BQ为底边的等腰三角形时:,如图2所示,
则秒,
秒
综上所述:当t为11秒或12秒时,是以BC或BQ为底边的等腰三角形. 【解析】用t可分别表示出BP和BQ,根据等腰三角形的性质可得到,可得到关于t的方程,可求得t;
用t分别表示出BQ和CQ,利用等腰三角形的性质可分和三种情况,分别得到关于t的方程,可求得t的值.
本题考查了勾股定理、等腰三角形的性质、方程思想及分类讨论思想等知识.用时间t表示出相应线段的长,化“动”为“静”是解决这类问题的一般思路,注意方程思想的应用.
相关试卷
这是一份2022-2023学年吉林省白城市大安市七年级(上)期末数学试卷,共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份吉林省白城市大安市2021-2022学年八年级(上)第一次月考数学试卷(解析版),共22页。试卷主要包含了选擇题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年吉林省白城市大安市七年级(上)期中数学试卷(含答案解析),共12页。试卷主要包含了94×1010B,5,12,−112,4,0,2,6×13)÷],【答案】B,【答案】−3,【答案】12h−12πa2,【答案】7或−1等内容,欢迎下载使用。









