2022-2023学年江苏省连云港市东海县八年级（上）期中数学试卷（含答案解析）

2022-2023学年江苏省连云港市东海县八年级（上）期中数学试卷

1.     甲骨文是中国的一种古代文字，是汉字的早期形式．下列甲骨文中，是轴对称图形的是(    )

A.  B.  C.  D.

2.     下列生活实物中，没有用到三角形的稳定性的是(    )

A.  B.
C.  D.

3.     下列说法正确的是(    )

A. 两个形状相同的图形称为全等图形 B. 两个圆是全等图形
C. 全等图形的形状、大小都相同 D. 面积相等的两个三角形是全等图形

4.     如图，小明家仿古家具的一块三角形形状的玻璃坏了，需要重新配一块．小明通过电话给玻璃店老板提供相关数据，为了方便表述，将该三角形记为，提供下列各组元素的数据，配出来的玻璃不一定符合要求的是(    )
    

A. AB，BC，CA B. AB，BC， C. AB，AC， D. ，，BC

5.     满足下列条件的三角形中，不是直角三角形的是(    )

A. 三内角之比为1：2：3 B. 三边长之比为2：2：3
C. 三边长之比为3：4：5 D. 三边长的平方之比为1：2：3

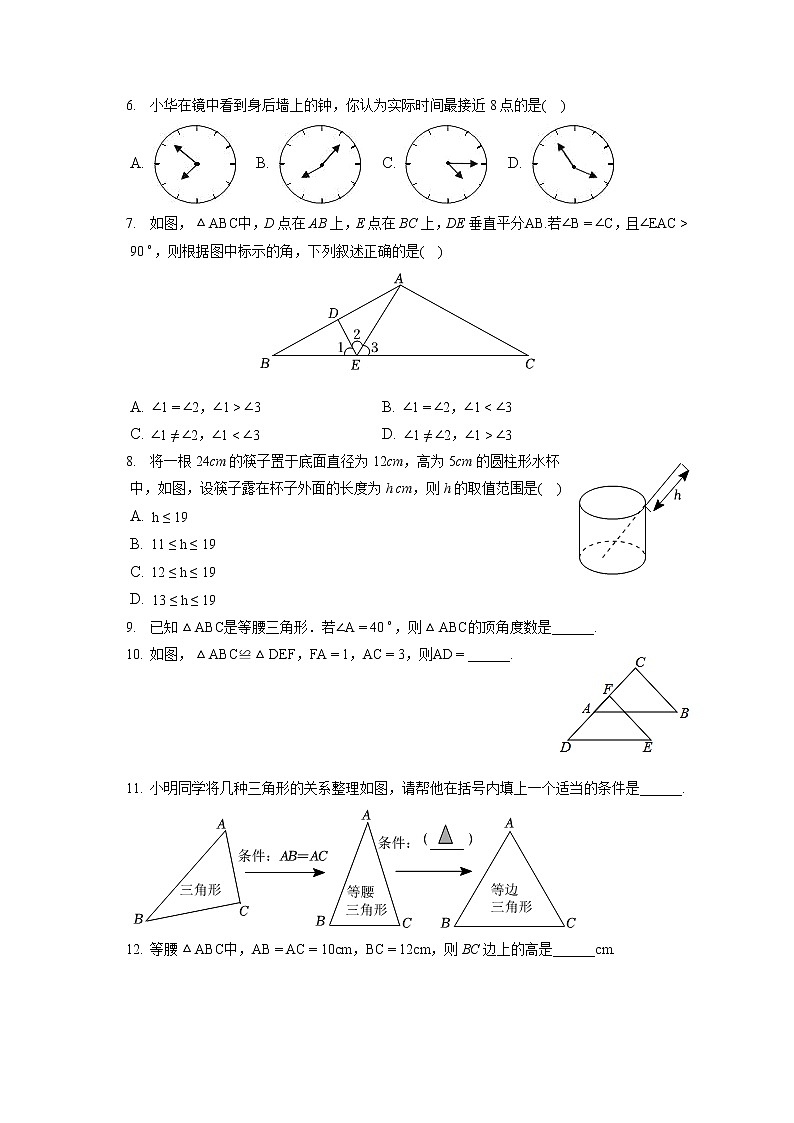
6.     小华在镜中看到身后墙上的钟，你认为实际时间最接近8点的是(    )

A.  B.  C.  D.

7.     如图，中，D点在AB上，E点在BC上，DE垂直平分若，且，则根据图中标示的角，下列叙述正确的是(    )

A. ， B. ，
C. ， D. ，

8.     将一根24cm的筷子置于底面直径为12cm，高为5cm的圆柱形水杯中，如图，设筷子露在杯子外面的长度为h cm，则h的取值范围是(    )

A.
B.
C.
D.

9.     已知是等腰三角形．若，则的顶角度数是______.
10. 如图，≌，，，则______.

11. 小明同学将几种三角形的关系整理如图，请帮他在括号内填上一个适当的条件是______.
     
12. 等腰中，，，则BC边上的高是______
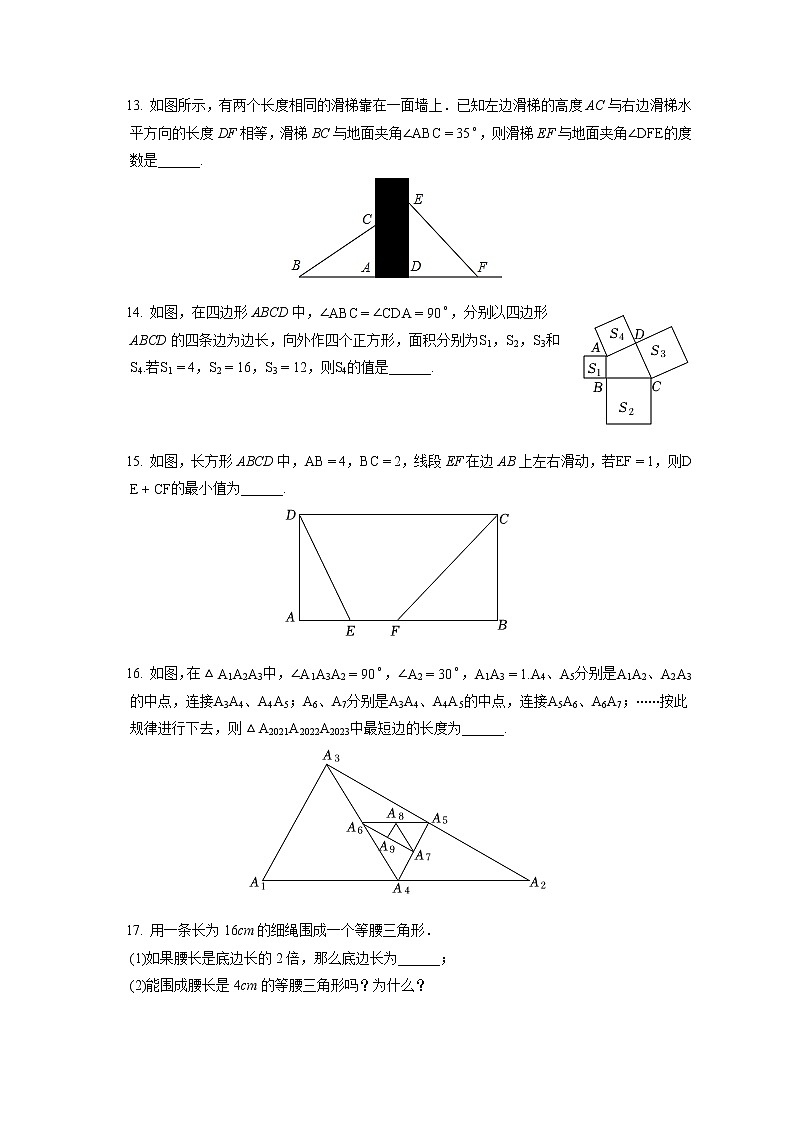
13. 如图所示，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，滑梯BC与地面夹角，则滑梯EF与地面夹角的度数是______.

14. 如图，在四边形ABCD中，，分别以四边形ABCD的四条边为边长，向外作四个正方形，面积分别为，，和若，，，则的值是______.

15. 如图，长方形ABCD中，，，线段EF在边AB上左右滑动，若，则的最小值为______.

16. 如图，在中，，，、分别是、的中点，连接、；、分别是、的中点，连接、；⋯⋯按此规律进行下去，则中最短边的长度为______.

17. 用一条长为16cm的细绳围成一个等腰三角形．
    如果腰长是底边长的2倍，那么底边长为______；
    能围成腰长是4cm的等腰三角形吗？为什么？
18. 如图，在的正方形网格中，每个小正方形的边长均为1，的三个顶点均在小正方形的顶点上．
    在图1中画点D在小正方形的顶点上，使与全等，且点D在直线AB的下方点D不与点C重合；
    在图2中画点E在小正方形的顶点上，使与全等，且；
    请直接写出的面积．
     
19. 如图，在中，点D在边BC上，，，求证：

20. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点和顶点为网格线的交点，以及过格点的直线
    将向右平移两个单位长度，再向下平移两个单位长度，画出平移后的三角形；
    画出关于直线l对称的三角形；
    观察画图结果，根据理解直接填空：______

21. 如图，已知，利用直尺和圆规作图．保留作图痕迹，不写作法
    作的角平分线AD；
    在的边AC上方作，在射线AE上截取，连接CD，直接写出CD和AB的关系．

22. 如图，BD是的角平分线，，交AB于点
    求证：
    当时，请判断CD与ED的大小关系，并说明理由．

23. 在创建“全国文明城市”期间，某小区在临街的拐角清理出了一块可以绿化的空地．如图，经技术人员的测量，已知，，，，若平均每平方米空地的绿化费用为100元，试计算绿化这片空地共需花费多少元？

24. 如图，中，，，点D在线段BC上，，，DE与AB相交于点F，延长BE到点N，使得，连接DN，交AB于点
    求证：；
    若，求DF的长．

25. 如图，已知在中，，，点P从B点出发沿射线BC以每秒1个单位的速度向右运动，设点P的运动时间为t，连接
    当秒时，求AP的长度；
    当为等腰三角形时，求t的值；
    请直接写出在点P的运动过程中，当t的值是多少时，PA平分？

26. 【问题呈现】在中，，，点D是斜边AB上的一点，连接CD，试说明AD、BD、CD之间的数量关系，并说明理由．
    【解决策略】小敏同学思考后是这样做的：将绕点C逆时针旋转，得到对应的，连接DE，如图1经过推理使问题得到解决．请回答：
    的形状是______，的形状是______；
    直接写出AD、BD、CD之间的数量关系是______；
    【方法感悟】在解决问题时，条件中若出现“等边三角形”、“等腰直角三角形”字样，可以考虑旋转某个三角形，把分散的条件或结论集中到一起，从而使问题得到解决．
    如图2，在四边形ABCD中，，连接对角线AC、BD，，，若，，求CA的长；
    如图3，在四边形ABCD中，，，若，，求A、C两点之间的最大距离．
    
    

答案和解析

1.【答案】C 

【解析】解：A、不是轴对称图形，故本选项不符合题意；
B、不是轴对称图形，故本选项不符合题意；
C、是轴对称图形，故本选项符合题意；
D、不是轴对称图形，故本选项不符合题意．
故选：
根据轴对称图形的概念对各选项分析判断即可得解．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 

2.【答案】B 

【解析】解：A、应用到三角形的稳定性，不符合题意；
B、没有应用到三角形的稳定性，符合题意；
C、应用到三角形的稳定性，不符合题意；
D、应用到三角形的稳定性，不符合题意；
故选：
根据三角形具有稳定性判断即可．
本题考查的是三角形的性质，熟记三角形具有稳定性是解题的关键．
 

3.【答案】C 

【解析】解：A、两个形状相同、大小相同的图形是全等图形，故原命题错误，不符合题意；
B、两个圆的形状相同但大小不相同，不是全等图形，故原命题错误，不符合题意；
C、全等图形的形状、大小都相同，正确，符合题意；
D、面积相等的两个三角形不一定是全等图形，故原命题错误，不符合题意．
故选：
利用全等图形的定义分别判断后即可确定正确的选项．
本题考查了全等图形的定义，解题的关键是了解能够完全重合的两个图形是全等图形，难度不大．
 

4.【答案】C 

【解析】解：根据三边分别相等的两个三角形全等，三角形形状确定，故此选项不合题意；
B.根据两边和它们的夹角分别相等的两个三角形全等，三角形形状确定，故此选项不合题意；
C.AB，AC，，无法确定三角形的形状，故此选项符合题意；
D.根据两角分别相等且其中一组等角的对边相等的两个三角形全等，三角形形状确定，故此选项不合题意；
故选：
直接利用全等三角形的判定方法分析得出答案．
此题主要考查了全等三角形的应用，正确掌握全等三角形的判定方法是解题关键．
 

5.【答案】B 

【解析】解：A、根据三角形内角和定理，求得各角分别为，，，故A选项是直角三角形，不符合题意；
B、，不符合勾股定理的逆定理，故B选项不是直角三角形，符合题意；
C、三边长之比为3：4：5时，符合勾股定理的逆定理，故C选项是直角三角形，不符合题意；
D、三边长的平方之比为1：2：3时，符合勾股定理的逆定理，故D选项是直角三角形，不符合题意；
故选：
根据三角形内角和公式和勾股定理的逆定理判定是否为直角三角形．
本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
 

6.【答案】D 

【解析】解：实际时间为8点的时针关于过12时、6时的直线的对称点是4点，
那么8点的时钟在镜子中看来应该是4点的样子，
所以应该是C或D答案之一，这两个答案中更接近八点的应该是第四个图形．
故选
此题考查镜面对称，根据镜面对称的性质，在平面镜中的钟面上的时针、分针的位置和实物应关于过12时、6时的直线成轴对称．
本题考查了镜面反射的原理与性质；这是一道开放性试题，解决此类题注意技巧．
 

7.【答案】A 

【解析】解：垂直平分AB，
，，
，
，
，
，
，，
，
，，
故选：
根据线段垂直平分线的性质，等腰三角形的性质解答即可．
本题主要考查了线段垂直平分线的性质和等腰三角形的性质，熟练掌握相关的性质定理是解答本题的关键．
 

8.【答案】B 

【解析】解：如图，当筷子的底端在D点时，筷子露在杯子外面的长度最长，
此时，
当筷子的底端在A点时，筷子露在杯子外面的长度最短，
在中，，，
，
此时，
所以h的取值范围是
故选：
当筷子的底端在A点时，筷子露在杯子外面的长度最短；当筷子的底端在D点时，筷子露在杯子外面的长度最长．然后根据勾股定理求出AB的长，即可解决问题．
本题考查了勾股定理的应用，能够读懂题意和求出h的值最大值与最小值是解题关键．
 

9.【答案】或 

【解析】解：当是顶角时，的顶角度数是；
当是底角时，则的顶角度数为；
综上，的顶角度数是或
故答案为：或
分是顶角和底角两种情况讨论，即可解答．
本题考查了等腰三角形的性质，此类题目，难点在于要分情况讨论．
 

10.【答案】2 

【解析】解：≌，
，
，
，，
，
故答案为：
直接利用全等三角形的对应边相等得到，进而得出答案．
此题主要考查了全等三角形的性质，正确得出对应边是解题的关键．
 

11.【答案】答案不唯一 

【解析】解：有一个角是的等腰三角形是等边三角形，
故答案为：答案不唯一
根据等边三角形的判定定理填空即可．
本题考查等边三角形的判定，解题的关键是掌握等边三角形的定义及等边三角形与等腰三角形的关系．
 

12.【答案】8 

【解析】解：如图，AD是BC边上的高线．
，，
，
在直角中，由勾股定理得到：
故答案是：
利用等腰三角形的“三线合一”的性质得到，然后在直角中，利用勾股定理求得高线AD的长度．
本题主要考查了等腰三角形的三线合一定理和勾股定理．等腰三角形底边上的高线把等腰三角形分成两个全等的直角三角形．
 

13.【答案】 

【解析】解：在和中，
，
，
，

故答案为：
利用“HL”证明和全等，根据全等三角形对应角相等可得，再根据直角三角形两锐角互余列式计算即可得解．
本题考查了全等三角形的应用，直角三角形两锐角互余的性质，准确识图判断出全等三角形是解题的关键．
 

14.【答案】8 

【解析】解：如图，连接AC，

由题意可知，，，
，
即，
，
故答案为：
由题意可知，，，得出，再代入数据即可求解．
本题考查了勾股定理，熟练掌握勾股定理是解题的关键．
 

15.【答案】5 

【解析】解：如图，作D关于AB的对称点，在CD上截取，然后连接交AB于E，在EB上截取，此时的值最小，

，，
四边形EFCH是平行四边形，
，
，
，，
，，
由勾股定理得：，
即的最小值为
故选答案为：
作D关于AB的对称点，在CD上截取，然后连接交AB于E，在EB上截取，此时的值最小，利用勾股定理即可求出．
此题主要考查了利用轴对称求最短路径问题以及勾股定理等知识，确定最小时E，F位置是解题关键．
 

16.【答案】 

【解析】解：在中，，，，
、分别是、的中点，

是的中点，
在中最短的边长度为，
在中最短的边长度为，
在中最短的边长度为，

在中最短的边长度为，
中最短边的长度为，
故答案为：
根据已知条件和图形的变化可得前几个图形中最短边的长度，找出规律，可得结论．
本题主要考查了规律型，图形的变化类，解决本题的关键是观察图形变化寻找规律．e
 

17.【答案】 

【解析】解：设底边长为xcm，则腰长为2xcm，则
解得，，
底边长为：；
故答案为：；
不能围成有长是4cm的等腰三角形，
当4cm为腰时，底边，因为，故不能构成三角形，故舍去；
故不能构成腰长为4cm的等腰三角形．
设底边长为xcm，则腰长为2xcm，根据周长公式列一元一次方程，解方程即可求得各边的长；
题中没有指明4cm所在边是底还是腰，故应该分情况进行分析，注意利用三角形三边关系进行检验．
此题主要考查等腰三角形的性质及三角形三边关系的综合运用，熟练掌握三角形的三边关系是解题的关键．
 

18.【答案】解：如图1，即为所求．
如图2，即为所求．

的面积为 

【解析】根据全等三角形的判定，取格点D，连接AD，BD即可．
在直线AB的上方取格点E，连接BE，AE，使四边形ACBE为平行四边形即可．
利用三角形的面积公式可得答案．
本题考查作图-应用与设计作图、全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解答本题的关键．
 

19.【答案】证明：在和中，
，
≌，
 

【解析】利用ASA证明≌，可得结论．
本题考查了全等三角形的判定与性质等知识，熟练掌握全等三角形的判定与性质是解题的关键．
 

20.【答案】45 

【解析】解：如图，即为所求；

如图，即为所求；
由图形知，，是等腰直角三角形，
，
故答案为：
根据平移的性质，即可画出；
根据轴对称的性质，即可画出；
作出等腰直角，即可求出答案．
本题主要考查了作图-平移变换，旋转变换，等腰直角三角形的性质等知识，熟练掌握平移和旋转的性质是解题的关键．
 

21.【答案】解：如图，AD即为所求．

如图，和AD即为所求．

，
，
，
四边形ABCD为平行四边形，
，且 

【解析】按照角平分线的作图方法作图即可．
按照作一个角等于已知角的作图方法，作，再以点A为圆心，BC的长为半径画弧，交射线AE于点D，连接CD即可．可判断出四边形ABCD为平行四边形，即可得，
本题考查作图-复杂作图、平行四边形的判定与性质，熟练掌握角平分线的作图方法、作一个角等于已知角的作图方法以及平行四边形的判定与性质是解答本题的关键．
 

22.【答案】证明：是的角平分线，
，
，
，

解：，理由如下：
，
，
，
，，
，
，
，
由得，，
，
 

【解析】利用角平分线的定义和平行线的性质可得结论；
利用平行线的性质可得，则，从而有，由得，，可知，等量代换即可．
本题主要考查了平行线的性质，等腰三角形的判定与性质，角平分线的定义等知识，熟练掌握平行与角平分线可推出等腰三角形是解题的关键．
 

23.【答案】解：，，，
，
，，
，
是直角三角形，，
，，
，
元，
答：绿化这片空地共需花费11400元． 

【解析】由勾股定理得出AC，再由勾股定理逆定理得出，然后由直角三角形面积求法得出这片空地的面积，即可得出答案．
此题主要考查了勾股定理的应用，熟练掌握勾股定理以及勾股定理逆定理是解题的关键．
 

24.【答案】证明：，，
，
又，
，
，，
，
，
；
解：，
，，
又，
，
在和中，
，
≌，
，
，
 

【解析】由线段中垂线的性质可得，由等腰三角形的性质可求，可得结论；
由“ASA”可证≌，可得
本题考查了全等三角形的判定和性质，线段垂直平分线的性质，等腰直角三角形的性质，证明三角形全等是解题的关键．
 

25.【答案】解：当时，，
，
，
在中，；
由题意可知，
当时，P点在BC上时，，
，
当时，，
解得；
当时，P点在BC的延长线上，，
，
当时，，
解得舍或；
当时，；
综上所述：t是的值为或30或17；
过点P作交于点E，
平分，
，
，，
，
≌，
，
，
，
在中，，
，
解得 

【解析】求出，再由勾股定理求AP的长即可；
分两种情况讨论：当时，P点在BC上时，；当时，P点在BC的延长线上，时，；时，；
过点P作交于点E，在中，，即，求出t的值即可．
本题考查三角形的综合应用，熟练掌握直角三角形的性质，角平分线的性质，等腰三角形的性质，勾股定理是解题的关键．
 

26.【答案】直角三角形  等腰直角三角形   

【解析】【解决策略】解：将绕点C逆时针旋转，得到对应的，
，，
是等腰直角三角形，
，
，
在和中，
，
≌，
，
，
，
是直角三角形，
故答案为：直角三角形，等腰直角三角形；
≌，
，
，
，
，
，
；
故答案为：；
【方法感悟】
过点D作，交CB的延长线于E，连接AE，如图2，

，
是直角三角形，
由可知≌，
，，
，
，
，，
，，
；
将绕点A顺时针旋转，得到对应的，连接CE，如图3，

，
，，
是等边三角形，
，
，
当C，B，E三点共线时，CE最大，
、C两点之间的最大距离是
【解决策略】
由旋转的性质得出是等腰直角三角形，证明≌，由全等三角形的性质得出，则可得出结论；
由全等三角形的性质得出结论；
【方法感悟】
过点D作，交CB的延长线于E，连接AE，证出，由勾股定理可得出答案；
将绕点A顺时针旋转，得到对应的，连接CE，则，证出，求出CE的最大值可得出答案．
本题是四边形综合题，考查了全等三角形的判定与性质，旋转的性质，等腰直角三角形的性质，勾股定理，熟练掌握全等三角形的判定与性质是解题的关键．