2022-2023学年浙江省绍兴市新昌县拔茅中学等五校八年级（上）期中数学试卷（含答案解析）

这是一份2022-2023学年浙江省绍兴市新昌县拔茅中学等五校八年级（上）期中数学试卷（含答案解析），共17页。试卷主要包含了5cm，5cm，5cm，10cm，5cmD，则S3=______，【答案】D，【答案】A，【答案】B，【答案】C等内容，欢迎下载使用。
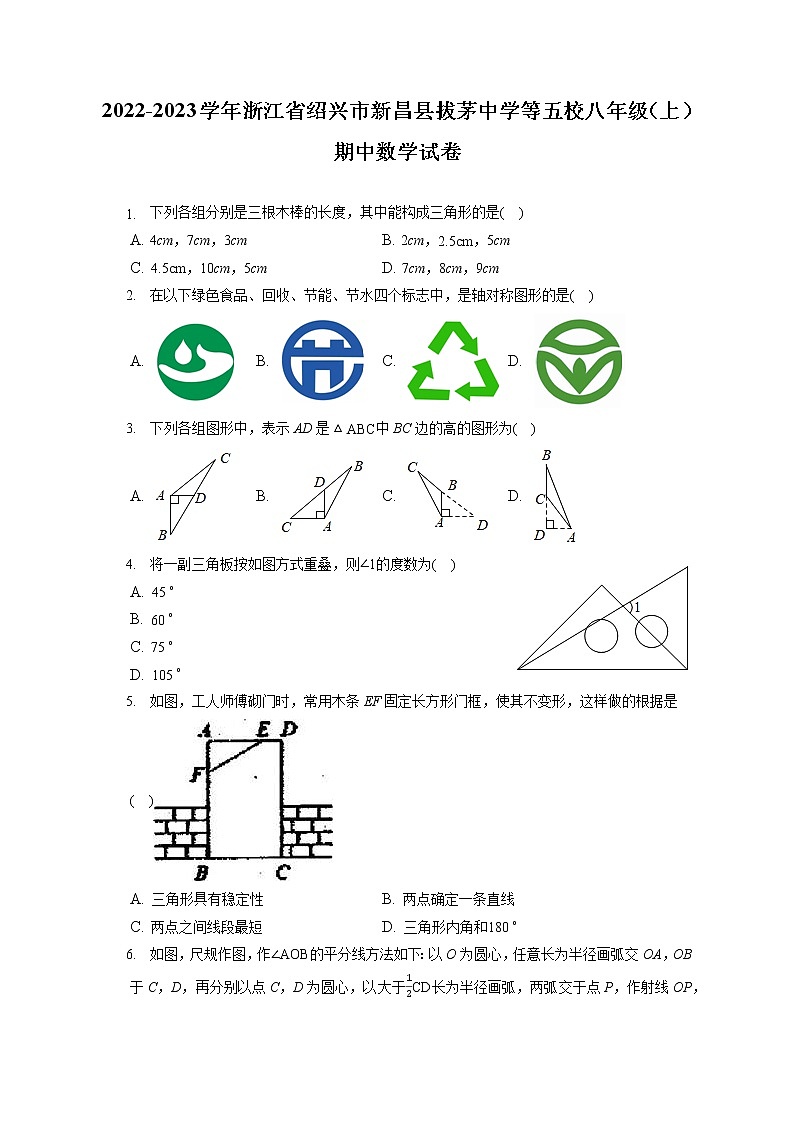
2022-2023学年浙江省绍兴市新昌县拔茅中学等五校八年级（上）期中数学试卷     下列各组分别是三根木棒的长度，其中能构成三角形的是(    )A. 4cm，7cm，3cm B. 2cm，，5cm
C. ，10cm，5cm D. 7cm，8cm，9cm    在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是(    )A.  B.  C.  D.     下列各组图形中，表示AD是中BC边的高的图形为(    )A.  B.  C.  D.     将一副三角板按如图方式重叠，则的度数为(    )A.
B.
C.
D.     如图，工人师傅砌门时，常用木条EF固定长方形门框，使其不变形，这样做的根据是(    )A. 三角形具有稳定性 B. 两点确定一条直线
C. 两点之间线段最短 D. 三角形内角和    如图，尺规作图，作的平分线方法如下：以O为圆心，任意长为半径画弧交OA，OB于C，D，再分别以点C，D为圆心，以大于长为半径画弧，两弧交于点P，作射线OP，由作法得≌的根据是     (    )
 A. SAS B. ASA C. AAS D. SSS    对于命题“若，则”，下面四组关于a，b的值中，能说明这个命题是假命题的是(    )A. ， B. ， C. ， D. ，    如图，DE是的边BC的垂直平分线，分别交边AB，BC于点D，E，且，，则的周长是(    )A.
B. 12
C. 15
D. 18    若一个等腰三角形的一条边是另一条边的k倍，我们把这样的等腰三角形叫做“k倍边等腰三角形”．如果一个等腰三角形是“4倍边等腰三角形”，且周长为18cm，则该等腰三角形底边长为(    )A. 12cm B. 12cm或2cm C. 2cm D. 4cm或12cm如图，M，A，N是直线l上的三点，，，P是直线l外一点，且，，若动点Q从点M出发，向点N移动，移动到点N停止，在形状的变化过程中，依次出现的特殊三角形是(    )
A. 直角三角形一等边三角形一直角三角形一等腰三角形
B. 直角三角形一等腰三角形一直角三角形一等边三角形
C. 等腰三角形一直角三角形一等腰三角形一直角三角形
D. 等腰三角形一直角三角形一等边三角形一直角三角形把命题“垂直于同一条直线的两直线平行”，改写成“如果…，那么…”的形式：______ .如图，是的一个外角，CE平分，若，，则的大小是______度．
 如图，点P是的平分线AD上一点，于点若，则点P到AB的距离是______.
 如图，点A，D，B，E在同一条直线上，，，要使≌，只需添加一个条件，这个条件可以是______.
 如图，中，，以的三边为边向外作正方形，其面积分别为，，，且，则______.
 如图，等腰三角形ABC中，，AD、BE是等腰三角形ABC的高线，连接DE，若，，则______.
如图，，点D，E分别在AC，AB上，且求证：
请将下列证明过程补充完整：
证明：在和中，
______
____________公共角
______已知
≌______
______
如图，中，AD是BC边上的高，AE是的平分线，，，求的度数.如图，，
求证：≌
线段EB与EC相等吗？请说明理由．
如图，在中，，，F为AB延长线上一点，点E在BC上，且
求证：
延长AE交CF于点D，请判断直线AE与CF的位置关系．
如图，在正方形网格中，点A、B、C、M、N都在格点上．
作关于直线MN对称的图形；
若网格中最小正方形的边长为1，求的面积；
在直线MN上找一点P，使的值最小，标出点P的位置保留作图痕迹
如图，已知中，，以点B为圆心，BC长为半径的弧分别交AC，AB于点D，E，连接BD，
写出图中所有的等腰三角形，并说明理由．
若，求的度数．
如图1，在中，AD为BC边上的中线，延长AD至E，使，连结求证：≌
如图2，在中，，，D为AB的中点，求的面积．
如图，在长方形ABCD中，，，点P从点B出发，以秒的速度沿BC向点C运动，设点P的运动时间为t秒：
______用t的代数式表示
当t为何值时，≌？
当点P从点B开始运动，同时，点Q从点C出发，以秒的速度沿CD向点D运动，是否存在这样v的值，使得与全等？若存在，请求出v的值；若不存在，请说明理由．

答案和解析 1.【答案】D 【解析】解：A、，不能围成三角形，故本选项不符合题意；
B、，不能围成三角形，故本选项不符合题意；
C、，不能围成三角形，故本选项不符合题意；
D、，能围成三角形，故本选项符合题意．
故选：
根据三角形的三边关系对各选项进行逐一分析即可．
本题考查的是三角形三边关系，即三角形任意两边之和大于第三边，任意两边之差小于第三边．
 2.【答案】D 【解析】解：选项A、B、C不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
选项D能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
故选：
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 3.【答案】D 【解析】解：的高AD是过顶点A与BC垂直的线段，只有D选项符合．
故选：
根据高的定义：”过三角形的顶点向对边作垂线，顶点和垂足之间的线段叫做三角形的高线“解答．
本题考查了三角形的高线，属于基础题，熟记概念是解题的关键．
 4.【答案】C 【解析】解：根据三角板的度数知，，，
，
故选：
直接利用一副三角板的内角度数，再结合三角形外角的性质得出答案．
此题主要考查了三角形的外角以及三角尺的特征，正确利用三角形外角的性质是解题关键．
 5.【答案】A 【解析】【分析】
本题考查三角形稳定性的实际应用，三角形的稳定性在实际生活中有着广泛的应用，要使一些图形具有稳定的结构，往往通过连接辅助线转化为三角形而获得．
当三角形三边的长度确定后，三角形的形状和大小就能唯一确定下来，故三角形具有稳定性．根据三角形的稳定性，可直接选择．
【解答】
解：加上EF后，原图形中具有了，
故这种做法根据的是三角形的稳定性．
故选  6.【答案】D 【解析】【分析】
本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角，认真阅读作法，从角平分线的作法得出与的两边分别相等，加上公共边相等，于是两个三角形符合SSS判定方法要求的条件，答案可得．
【解答】
解：以O为圆心，任意长为半径画弧交OA，OB于C，D，即；
以点C，D为圆心，以大于长为半径画弧，两弧交于点P，即；
在和中，
，
≌
故选  7.【答案】B 【解析】【分析】
本题主要考查假命题的判断，举反例是说明假命题不成立的常用方法，但需要注意所举反例需要满足命题的题设，但结论不成立。
说明命题为假命题，即a、b的值满足，但不成立，把四个选项中的a、b的值分别代入验证即可.
【解答】
解：A、，，且，满足“若，则”，故A选项不符合题意；
B、，，且，此时虽然满足，但不成立，故B选项符合题意；
C、，，且，满足“若，则”，故C选项不符合题意；
D、，，此时不满足，故D选项不符合题意.
故选  8.【答案】C 【解析】解：是的边BC的垂直平分线，
，
的周长，
，，
的周长，
故选：
由DE是的边BC的垂直平分线，可得，则所求的周长，再将已知代入即可．
本题考查线段垂直平分线的性质，熟练掌握线段垂直平分线的性质是解题的关键．
 9.【答案】C 【解析】解：设该等腰三角形的较短边长为，则较长边长为
①当x cm为腰时，
，
，x，4x不能组成三角形；
②当4x cm为腰时，4x，4x，x能够组成三角形，
，
，
该等腰三角形底边长为
故选：
设该等腰三角形的较短边长为，则较长边长为分①x cm为腰；②4x cm为腰两种情况讨论即可．
本题考查了等腰三角形的性质，三角形三边关系定理，进行分类讨论是解题的关键．
 10.【答案】D 【解析】【分析】
本题考查了等边三角形的性质与判定，等腰三角形的判定与性质，熟练掌握等边三角形和等腰三角形的判定与性质是解题的关键．
把点Q从点M出发，沿直线l向点N移动，移动到点N停止的整个过程，逐次考虑确定三角形的形状即可判断．
【解答】
解：当点Q移动到，此时Q在A的左侧，且，是等腰三角形，
当点Q移动到点A的右侧，且时，是直角三角形，
当点Q移动到点A的右侧，且时，是等边三角形，
当点Q移动到点A的右侧，且时，是直角三角形，
在形状的变化过程中，依次出现的特殊三角形是：等腰三角形一直角三角形一等边三角形一直角三角形，
故选：  11.【答案】如果两条直线垂直于同一条直线，那么这两条直线平行 【解析】【分析】
命题由题设和结论两部分组成．题设是已知事项，结论是由已知事项推出的事项．命题常常可以写为“如果…那么…”的形式，如果后面接题设，而那么后面接结论．根据命题的定义来写．如果后面接题设，而那么后面接结论．
【解答】
解：把命题“垂直于同一条直线的两直线平行”，改写成“如果…，那么…”的形式：如果两条直线垂直于同一条直线，那么这两条直线平行．
故答案为：如果两条直线垂直于同一条直线，那么这两条直线平行．  12.【答案】50 【解析】解：是的一个外角，，，
，
平分，
，
故答案为：
根据角平分线的定义得到，利用三角形的外角性质解答即可．
本题考查的是三角形的外角的性质，掌握角平分线的定义是解题的关键．
 13.【答案】5 【解析】解：作于F，
是的平分线，，，
，
故答案为：
作于F，根据角平分线的性质解答即可．
本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
 14.【答案】答案不唯一 【解析】解：添加
，
，
，
在和中，
，
≌，
故答案为：答案不唯一
根据全等三角形的判定方法可以由SAS证明≌
本题主要考查了全等三角形的判定，解题的关键是掌握AAS，SAS证明两个三角形全等，此题难度不大．
 15.【答案】20 【解析】解：由勾股定理得，
，
，
，
故答案为：
利用勾股定理得，再根据正方形的面积公式可得答案．
本题主要考查了勾股定理，正方形的面积等知识，熟练掌握勾股定理是解题的关键．
 16.【答案】 【解析】解：是的高，
，
，，
，
，
，
，，

故答案为：
先根据等腰可知，由勾股定理计算BE和BC的长，最后由直角三角形斜边中线的性质可得DE的长．
本题考查了等腰三角形的性质，勾股定理，直角三角形斜边中线的性质，掌握等腰三角形三线合一的性质是本题的关键．
 17.【答案】已知  BAD CAE AE SAS 全等三角形的对应边相等 【解析】证明：在和中，
，
≌，
全等三角形的对应边相等，
故答案为：已知，BAD，CAE，AE，SAS，全等三角形的对应边相等．
由“SAS”可证≌，可得
本题考查了全等三角形的判定和性质，掌握三角形全等判定方法是解题的关键．
 18.【答案】解：是BC边上的高，，
，
，
，
是的角平分线，
，
 【解析】本题考查了三角形的角平分线、中线和高，主要利用了直角三角形两锐角互余，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记各性质并准确识图是解题的关键．
根据直角三角形两锐角互余求出，再根据三角形的一个外角等于与它不相邻的两个内角的和求出，然后根据角平分线的定义求出，再利用三角形的内角和定理列式计算即可得解．
 19.【答案】证明：在与中，
，
≌；
解：理由如下：
≌，
，
 【解析】根据SSS定理证明结论；
由中全等三角形得，再由等角对等边定理得结论．
本题考查了全等三角形的性质与判定，等腰三角形的判定，关键是掌握全等三角形的判定与性质．
 20.【答案】证明：，
，
在和中，
，
；
解：，理由如下：

≌，
，
，
，
，
，
 【解析】由，，，即可利用HL证得；
由全等三角形得，再由，得，即可得结论．
本题考查了全等三角形的判定与性质，利用HL证得是解题的关键．
 21.【答案】解：如图，即为所求；
的面积为：；

如图，点P即为所求． 【解析】根据轴对称的性质即可作出；
根据网格即可求的面积；
连接交直线MN于点P，此时的值最小．
本题考查了作图-轴对称变换，轴对称-最短路径问题，三角形的面积，解决本题的关键是掌握轴对称的性质准确作出点
 22.【答案】解：，
，
是等腰三角形；
，
，是等腰三角形；
图中所有的等腰三角形有：，，；
，

，

 【解析】根据等腰三角形的判定，两底角相等或两条边相等的三角形是等腰三角形，即可找出图中所有的等腰三角形；
根据等腰三角形的性质可求得，，在中可求得
此题考查了等腰三角形的判定与性质，三角形内角和定理，难度一般．
 23.【答案】证明：如图1中，

在和中，
，
≌；

解：如图2中，延长CD到T，使得，连接

由可知≌，
，，
，
，
 【解析】根据SAS证明三角形全等；
如图2中，延长CD到T，使得，连接由可知≌，推出，，利用勾股定理求出CT，即可解决问题．
本题考查了全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
 24.【答案】


当时，≌，
理由：，，
≌，
，
，
，
①当≌时，
，，
，
，
，
，
解得：，
，
，
解得：；
②当≌时，
，
，
，
，
解得：，
，
，
解得：
综上所述：当或时，与全等． 【解析】解：点P从点B出发，以秒的速度沿BC向点C运动，点P的运动时间为t秒时，，
则；
见答案；
见答案.
【分析】
根据P点的运动速度可得BP的长；
根据全等三角形的性质即可得出即可；
此题主要分两种情况①≌得到，，②≌得到，，然后分别计算出t的值，进而得到v的值．
此题是四边形综合题，主要考查了全等三角形的性质，矩形的性质，解本题的关键是全等三角形性质的掌握．