沪科版八年级上册第11章 平面直角坐标系综合与测试当堂达标检测题

2021-2022学年八年级数学上册尖子生同步培优题典【沪科版】

专题11.6平面直角坐标系大题专练（重难点培优）

姓名：__________________     班级：______________   得分：_________________

注意事项：

本试卷试题共30题，解答30道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．

三、解答题（本大题共30小题，解答时应写出文字说明、证明过程或演算步骤）

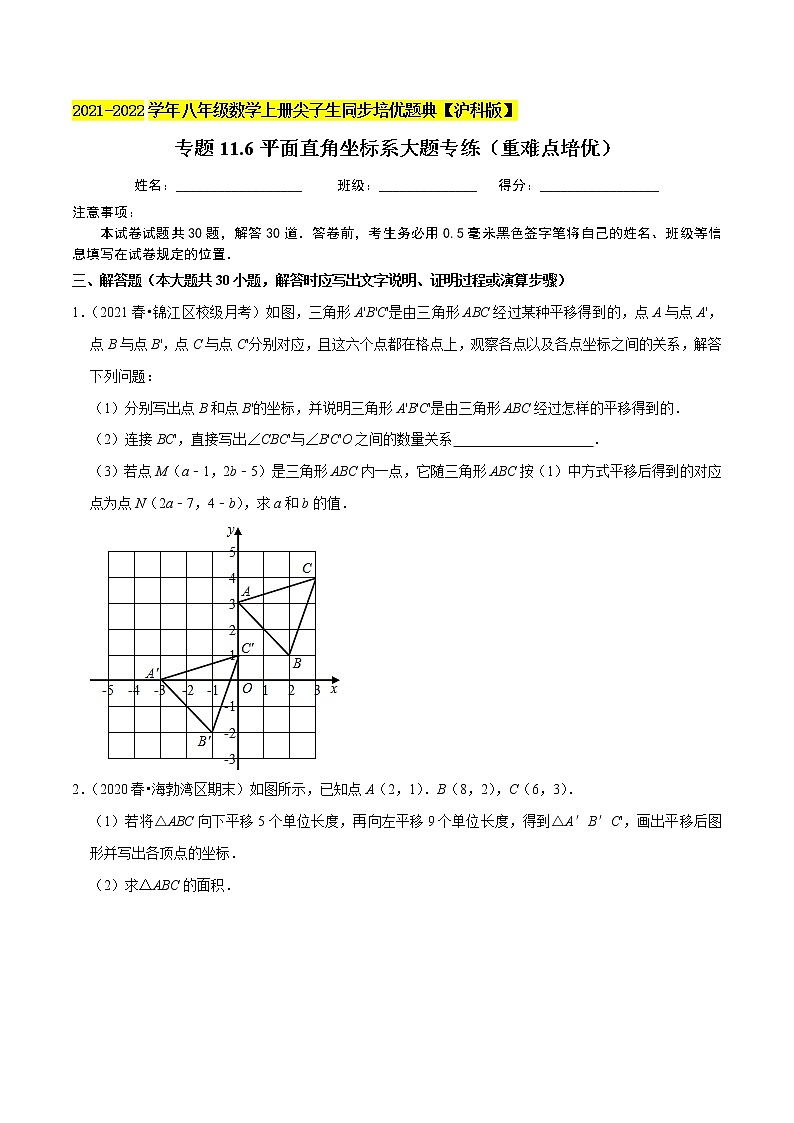
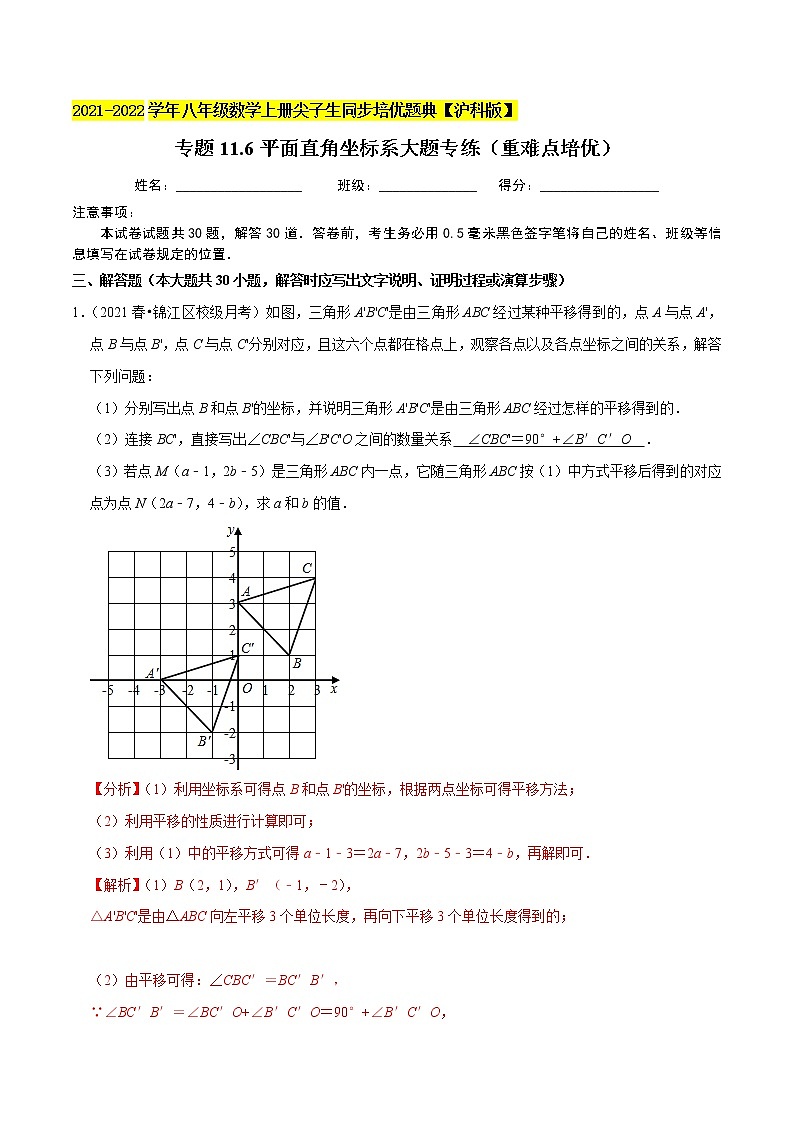
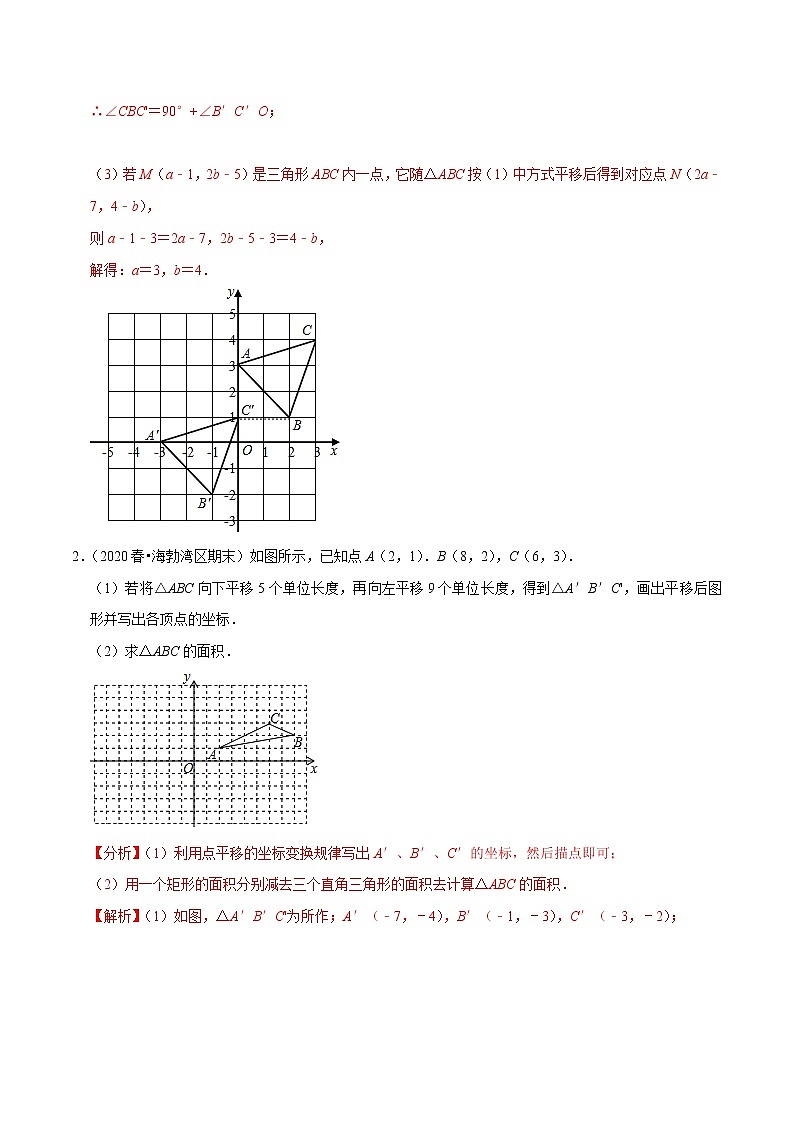
1．（2021春•锦江区校级月考）如图，三角形A'B'C'是由三角形ABC经过某种平移得到的，点A与点A'，点B与点B'，点C与点C'分别对应，且这六个点都在格点上，观察各点以及各点坐标之间的关系，解答下列问题：

（1）分别写出点B和点B'的坐标，并说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的．

（2）连接BC'，直接写出∠CBC'与∠B'C'O之间的数量关系　                　．

（3）若点M（a﹣1，2b﹣5）是三角形ABC内一点，它随三角形ABC按（1）中方式平移后得到的对应点为点N（2a﹣7，4﹣b），求a和b的值．

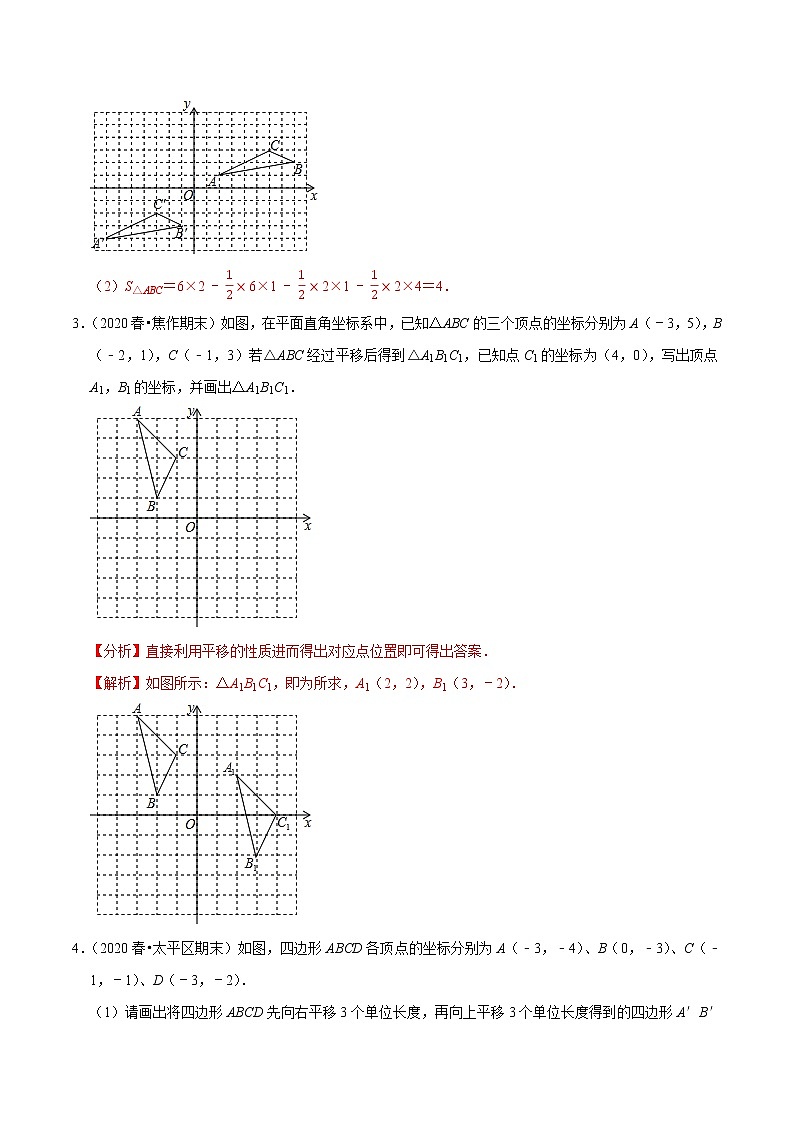
2．（2020春•海勃湾区期末）如图所示，已知点A（2，1）．B（8，2），C（6，3）．

（1）若将△ABC向下平移5个单位长度，再向左平移9个单位长度，得到△A′B′C'，画出平移后图形并写出各顶点的坐标．

（2）求△ABC的面积．

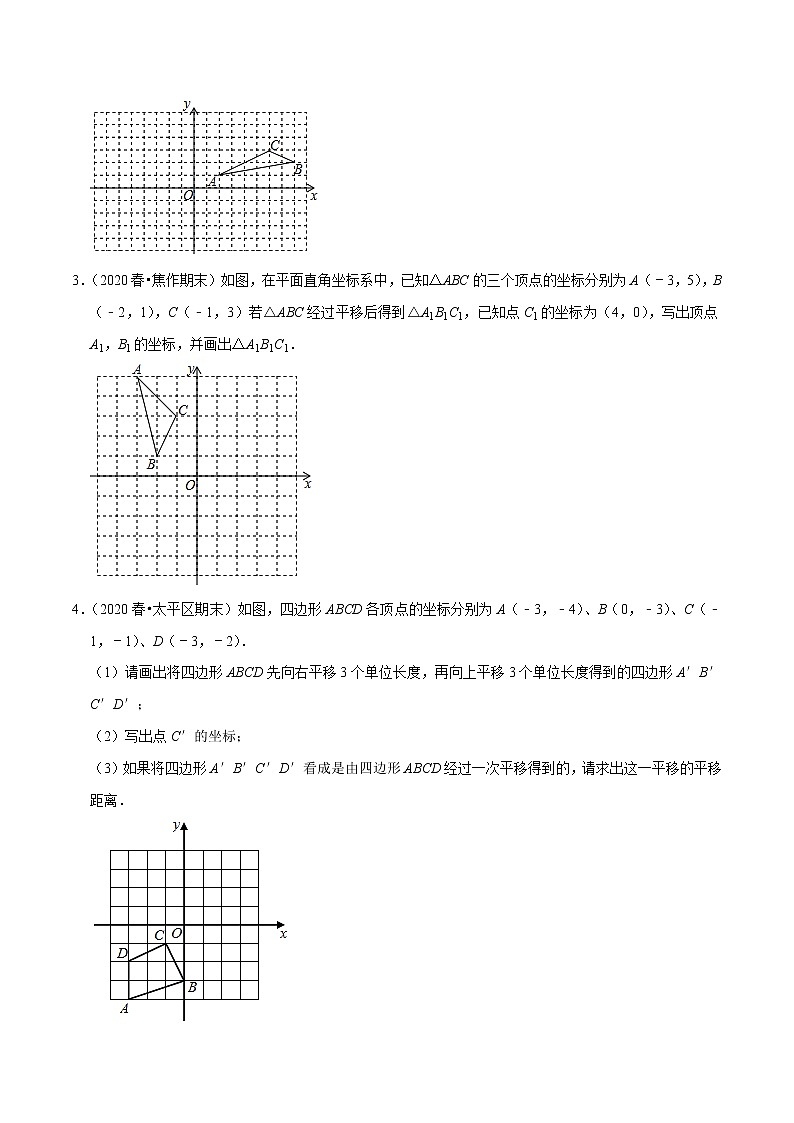
3．（2020春•焦作期末）如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）若△ABC经过平移后得到△A1B1C1，已知点C1的坐标为（4，0），写出顶点A1，B1的坐标，并画出△A1B1C1．

4．（2020春•太平区期末）如图，四边形ABCD各顶点的坐标分别为A（﹣3，﹣4）、B（0，﹣3）、C（﹣1，﹣1）、D（﹣3，﹣2）．

（1）请画出将四边形ABCD先向右平移3个单位长度，再向上平移3个单位长度得到的四边形A′B′C′D′；

（2）写出点C′的坐标；

（3）如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的，请求出这一平移的平移距离．

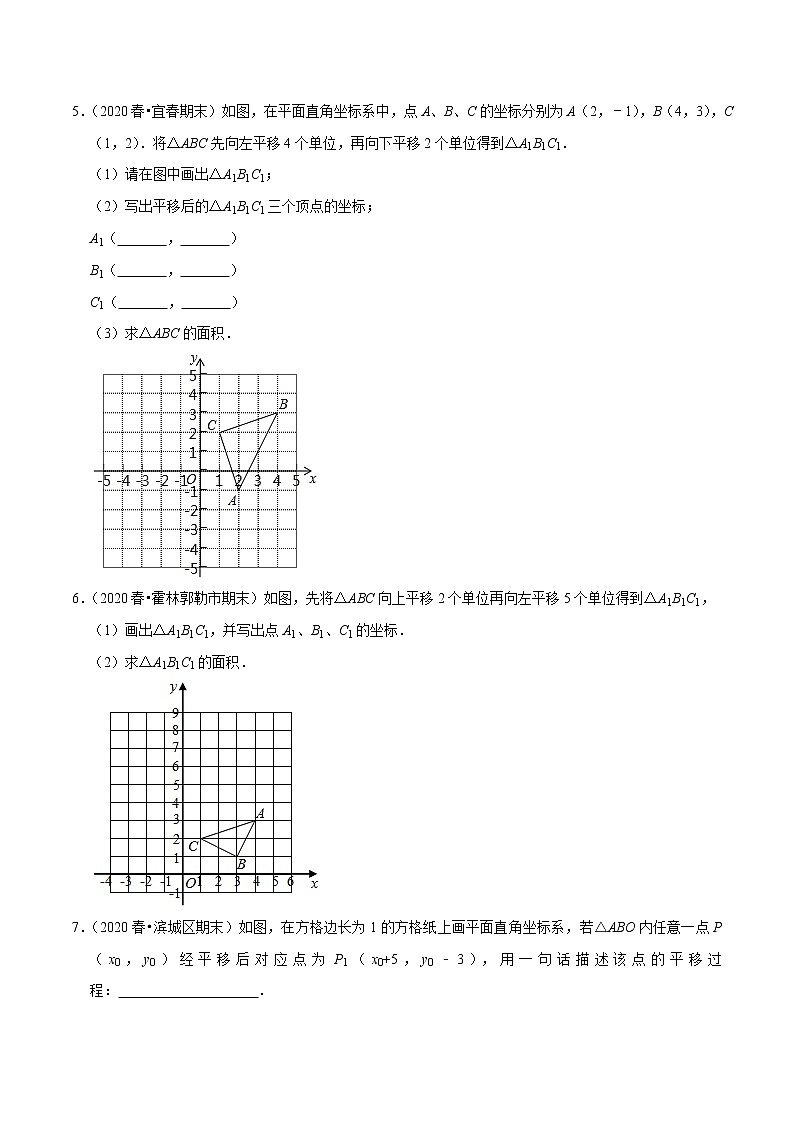
5．（2020春•宜春期末）如图，在平面直角坐标系中，点A、B、C的坐标分别为A（2，﹣1），B（4，3），C（1，2）．将△ABC先向左平移4个单位，再向下平移2个单位得到△A1B1C1．

（1）请在图中画出△A1B1C1；

（2）写出平移后的△A1B1C1三个顶点的坐标；

A1（　   　，　   　）

B1（　   　，　   　）

C1（　   　，　   　）

（3）求△ABC的面积．

6．（2020春•霍林郭勒市期末）如图，先将△ABC向上平移2个单位再向左平移5个单位得到△A1B1C1，

（1）画出△A1B1C1，并写出点A1、B1、C1的坐标．

（2）求△A1B1C1的面积．

7．（2020春•滨城区期末）如图，在方格边长为1的方格纸上画平面直角坐标系，若△ABO内任意一点P（x0，y0）经平移后对应点为P1（x0+5，y0﹣3），用一句话描述该点的平移过程：　                　．

若将△ABC作同样的平移得到△A1B1C1．完成下面问题：

（1）画出△A1B1C1，并写出A1，B1，C1的坐标；

（2）求△A1B1C1的面积．

8．（2020春•单县期末）如图，在平面直角坐标系中，△ABC的三个顶点分别是A（4，0），B（1，﹣5），C（5，﹣3），点A经过平移后对应点为A1（0，6），将△ABC作同样的平移得到△A1B1C1．

（1）若BC边上一点P（x，y）经过上述平移后的对应点为P1，用含x，y的式子表示点P1的坐标为　          　（直接写出结果即可）．

（2）画出平移后的△A1B1C1；

（3）求平移距离．

9．（2020春•兴城市期末）把三角形ABC放在直角坐标系中如图所示，现将三角形ABC向上平移1个单位长度，再向右平移3个单位长度就得到三角形A1B1C1．

（1）在图中画出三角形A1B1C1，并写出A1、B1、C1的坐标；

（2）点P在x轴上，且三角形PAC与三角形ABC面积相等，请直接写出点P的坐标．

10．（2020春•濮阳期末）如图，在平面直角坐标系中，已知A（﹣2，2），B（2，0），C（3，3），P（a，b）是三角形ABC的边AC上的一点，把三角形ABC经过平移后得三角形DEF，点P的对应点为P'（a﹣2，b﹣4）．

（1）写出D，E，F三点的坐标；

（2）画出三角形DEF；

（3）求三角形DEF的面积．

11．（2020春•昭通期末）如图，在平面直角坐标系xOy中，三角形ABC三个顶点的坐标分别为A（﹣2，﹣2），B（3，1），C（0，2）．点P（a，b）是三角形ABC的边AC上任意一点，三角形ABC经过平移后得到三角形A′B′C′，点P的对应点为P′（a﹣2，b+3）．

（1）写出点A′的坐标：点A′　       　．

（2）在图中画出平移后的三角形A′B′C′；

（3）三角形ABC的面积为　       　．

12．（2020春•荔城区期末）在平面直角坐标系中，△ABC的位置如图所示，把△ABC先向右平移3个单位，再向下平移4个单位可以得到△A'B'C'．

（1）画出平移后的图形△A′B′C′；

（2）请写出平移后A′B′C′的各个顶点A′，B′，C′的坐标．

13．（2020春•浦北县期末）如图，点A，B，C都落在网格的顶点上．

（1）写出点A，B，C的坐标；

（2）求三角形ABC的面积；

（3）把三角形ABC先向左平移4个单位长度，再向下平移5个单位长度，得三角形A'B'C'，画出三角形A'B'C'．

14．（2020春•洛阳期末）如图，△ABC在建立了平面直角坐标系的方格纸中，方格纸中的每个小方格都是边长为1个单位长度的正方形．

（1）请写出△ABC各顶点的坐标；

（2）直接写出△ABC的面积；

（3）把△ABC平移得到△A′B′C′，点B经过平移后对应点为B′（6，5），请在图中画出△A′B′C′．

15．（2020春•花都区期末）如图，在直角坐标系中，已知A（﹣1，4），B（﹣2，1），C（﹣4，1），将△ABC向右平移3个单位再向下平移2个单位得到△A1B1C1，点A、B、C的对应点分别是点A1、B1、C1．

（1）画出△A1B1C1；

（2）直接写出点A1、B1、C1的坐标；

（3）直接写出△A1B1C1的面积．

16．（2020春•澄迈县期末）在如图的方格纸中，三角形ABC的顶点均在格点上，建立平面直角坐标系后，点A、B的坐标分别为（﹣4，1）、（﹣2，0），三角形ABC内任意一点P的坐标为（a，b）

（1）三角形ABC向右平移　 　个单位长度到△A1B1C1位置，点C对应点C1的坐标为（　 　）：点P对应点P1的坐标为（　 　）（用含a、b的代数式表示）；

（2）三角形ABC经平移后点P的对应点为P2（a+3，b﹣4），请画出上述平移后的三角形A2B2C2，并写出点A2、B2的坐标．

17．（2020春•海淀区校级期末）如图，在平面直角坐标系xOy中，三角形ABC三个顶点的坐标分别为A（﹣5，1），B（﹣4，4），C（﹣1，﹣1）．将三角形ABC向右平移5个单位长度，再向下平移4个单位长度，得到三角形A'B'C'，其中点A'，B'，C'分别为点A，B，C的对应点．

（1）请在所给坐标系中画出三角形A'B'C'，并直接写出点C'的坐标；

（2）若AB边上一点P经过上述平移后的对应点为P'（x，y），用含x，y的式子表示点P的坐标；（直接写出结果即可）

（3）求三角形A'B'C'的面积．

解：（1）点C'的坐标为　       　；

（2）点P的坐标为　       　；

（3）　       　．

18．（2020春•大同期末）综合与实践

问题背景

如图，在平面直角坐标系中，点A的坐标为（﹣3，5），点B的坐标为（0，1），点C的坐标为（4，5），将线段AB沿AC方向平移，平移距离为线段AC的长度．

动手操作

（1）画出AB平移后的线段CD，直接写出B的对应点D的坐标；

探究证明

（2）连接BD，试探究∠BAC，∠BDC的数量关系，并证明你的结论；

拓展延伸

（3）若点E在线段BD上，连接AD，AE，且满足∠EAD＝∠CAD，请求出∠ADB：∠AEB的值，并写出推理过程．

19．（2020春•天门期末）已知三角形ABC的顶点分别为A（﹣4，﹣1），B（﹣5，﹣4），C（﹣1，﹣3），三角形A′B′C′是三角形ABC经过平移得到的，三角形ABC中任意一点P（x，y）平移后的对应点为P'（x+6，y+4）．

（1）请写出三角形ABC平移的过程；

（2）写出点A′，C′的坐标；

（3）请在图中建立直角坐标系，求三角形A′B′C′的面积．

20．（2020春•娄星区期末）如图，△ABC在直角坐标系中，

（1）请写出△ABC各顶点的坐标．

（2）若把△ABC向上平移2个单位，再向右平移3个单位得到△A1B1C1，请在图中画出△A1B1C1，并写出点A1、B1、C1的坐标．

（3）求出△ABC的面积．

21．（2020春•玉溪期末）如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（﹣4，3），B（﹣2，4），C（﹣1，1），若把△ABC向右平移5个单位长度，再向下平移3个单位长度得到△A'B'C'，点A，B，C的对应点分别为A'，B'，C'．

（1）写出A'，B'，C'的坐标；

（2）在图中画出平移后的△A'B'C'；

（3）求△A'B'C'的面积．

22．（2020春•玉州区期末）如图，在直角坐标系中，△ABC的顶点都在网格点上，其中C点的坐标为（1，2）．

（1）直接写出点B的坐标为　      　；

（2）求△ABC的面积；

（3）将△ABC向左平移1个单位，再向上平移2个单位，画出平移后的△A1B1C1，并写出△A1B1C1三个顶点的坐标．

23．（2020春•江汉区期末）如图所示，在平面直角坐标系中，△ABC的三个顶点A、B、C的坐标分别是A（﹣3，3）、B（﹣5，﹣1）、C（﹣1，1）；点P（m，n）是△ABC内部的一点，平移△ABC，点P随△ABC一起平移，点A、B、C、P的对应点的分别是A'、B'、C'、P'．若点P'坐标为（m+5，n﹣2）．

（1）画出平移后的△A'B'C'；

（2）连接BB'、CA'，已知A'B'交x轴于点M，则四边形CBB'A'的面积为　   　；点M的坐标为　   　；

（3）已知A'C'交x轴于点N，若P'恰好在线段B'N上，且满足S△P′MN＝2S△A′MN，则此时P的坐标为　   　．（说明：S△P′MN表示三角形P'MN的面积，后面类似）

24．（2020春•石泉县期末）如图，三角形A′B'C'是由三角形ABC平移得到的．

（1）若点P（a，b）是三角形ABC内部一点，求平移后三角形A′B′C'内的对应点P′的坐标

（2）画出将三角形ABC向左平移4个单位，再向下平移1个单位得到的三角形A1B1C1．

25．（2020春•红河州期末）如图，在边长为1个单位长度的小正方形网格中建立平面直角坐标系．已知三角形ABC的顶点A的坐标为A（﹣1，4），顶点B的坐标为（﹣4，3），顶点C的坐标为（﹣3，1）．

（1）把三角形ABC向右平移5个单位长度，再向下平移4个单位长度得到三角形A′B′C′，请你画出三角形A′B′C′；

（2）请直接写出点A′，B′，C′的坐标；

（3）求三角形ABC的面积．

26．（2020春•金乡县期末）在平面直角坐标系中，点A的坐标为（0，4），线段MN的位置如图所示，其中点M的坐标为（﹣3，﹣1），点N的坐标为（3，﹣2）．

（1）将线段MN平移得到线段AB，其中点M的对应点为A，点N的对应点为B．

①点M平移到点A的过程可以是：先向　 　平移　 　个单位长度，再向　 　平移　 　个单位长度；

②点B的坐标为　 　；

（2）在（1）的条件下，若点C的坐标为（4，0），连接AC，BC，求△ABC的面积．

（3）在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为3，若存在，请直接写出点P的坐标；若不存在，请说明理由．

27．（2020春•鞍山期末）如图，在平面直角坐标系中，点A的坐标是（﹣1，0），点B的坐标是（4，0），现将线段AB向右平移一个单位，向上平移4个单位，得到线段CD，点P是y轴上的动点，连接BP；

（1）当点P在线段OC上时（如图一），判断∠CPB与∠PBA的数量关系；

（2）当点P在OC所在的直线上时，连接DP（如图二），试判断∠DPB与∠CDP，∠PBA之间的数量关系，请直接写出结论．

28．（2020春•嘉祥县期末）（1）如图，在平面直角坐标系中有一个三角形ABC，请写出它的三个顶点坐标．A．　      　、B　      　、C　      　．

（2）在平面直角坐标系中描出以下3个点：A'（﹣2，1）、B'（1，﹣1）、C'（﹣3，﹣3），然后顺次连接A'、B'、C'，得到三角形A'B'C'．

（3）观察所画的图形，判断三角形A'B'C'能否由三角形ABC平移得到，如果能，请说出三角形A'B'C'是由三角形ABC怎样平移得到的；如果不能，说明理由．

29．（2020春•桃江县期末）如图，△ABC的三个顶点坐标分别为A（0，2），B（﹣3，1），C（﹣2，﹣2）．

（1）将△ABC向右平移2个单位，作出△A'B'C'；

（2）写出△A'B'C'的顶点坐标．

30．（2020春•通山县期末）如图，在平面直角坐标系中，点A（2，6），B（4，3），将线段AB进行平移，使点A刚好落在x轴的负半轴上，点B刚好落在y轴的负半轴上，A，B的对应点分别为A'，B'，连接AA'交y轴于点C，BB'交x轴于点D．

（1）线段A'B'可以由线段AB经过怎样的平移得到？并写出A'，B'的坐标；

（2）求四边形AA'B'B的面积；

（3）P为y轴上的一动点（不与点C重合），请探究∠PCA′与∠A'DB'的数量关系，给出结论并说明理由．