




数学八年级上册第11章 平面直角坐标系综合与测试单元测试达标测试
展开2021-2022学年八年级数学上册尖子生同步培优题典【沪科版】
专题11.8第11章 平面直角坐标系单元测试(能力过关卷)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分120分,考试时间90分钟,试题共26题,选择10道、填空8道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2021•长春模拟)在平面直角坐标系中,点(﹣2,﹣3)到x轴的距离是( )
A.﹣2 B.﹣3 C.2 D.3
【分析】根据点的纵坐标的绝对值是点到x轴的距离,可得答案.
【解析】在平面直角坐标系中,点(﹣2,﹣3)到x轴的距离为3.
故选:D.
2.(2021春•裕华区校级期末)已知点P(m,n)在第三象限,则点Q(﹣m,|n|)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据第三象限点的横坐标与纵坐标都是负数,然后判断点Q所在的象限即可.
【解析】∵点P(m,n)在第三象限,
∴m<0,n<0,
∴﹣m>0,|n|>0,
∴点Q(﹣m,|n|)在第一象限.
故选:A.
3.(2021春•武安市期末)已知点P(x,y)为第四象限内一点,且满足|x|=3,y2=4,则P点的坐标为( )
A.(﹣3,2) B.(3,2) C.(3,﹣2) D.(﹣3,﹣2)
【分析】点在第四象限内,那么其横坐标大于0,纵坐标小于0,进而根据所给的条件判断具体坐标.
【解析】∵点P(x,y)在第四象限,
∴x>0,y<0,
又∵|x|=3,y2=4,
∴x=3,y=﹣2,
∴点P的坐标是(3,﹣2).
故选:C.
4.(2020秋•会宁县期末)点P(a,b)在第四象限,且|a|>|b|,那么点Q(a+b,a﹣b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】直接利用各象限内点的坐标特点得出a,b的符号,进而结合绝对值的性质得出a+b,a﹣b的符号即可得出答案.
【解析】∵点P(a,b)在第四象限,且|a|>|b|,
∴a>0,b<0,a+b>0,a﹣b>0,
∴点Q(a+b,a﹣b)在第一象限.
故选:A.
5.(2021春•任丘市期末)如图,象棋盘上“将”位于点(2,﹣1),“象”位于点(4,﹣1),则“炮”位于点( )
A.(1,2) B.(2,﹣1) C.(﹣1,2) D.(2,1)
【分析】直接利用已知点坐标得出原点位置,进而得出答案.
【解析】如图所示:“炮”位于点(﹣1,2).
故选:C.
6.(2020春•海淀区校级期末)如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见,一号暗堡的坐标为(4,2),四号暗堡的坐标为(﹣2,4),原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大约是( )
A.A处 B.B处 C.C处 D.D处
【分析】直接利用已知点坐标得出原点位置进而得出答案.
【解析】如图所示:敌军指挥部的位置大约是B处.
故选:B.
7.(2017秋•深圳校级期中)在平面直角坐标系中,将点A(a,b)纵坐标乘以﹣1,得到点A′,则点A与点A′的关系是( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.将点A向x轴负方向平移一个单位得点A′
【分析】直接利用关于x轴对称点的性质得出答案.
【解析】将点A(a,b)纵坐标乘以﹣1,得到点A′,则点A与点A′的关系是:关于x轴对称.
故选:A.
8.(2020秋•建平县期末)若xy>0,则关于点P(x,y)的说法正确的是( )
A.在一或二象限 B.在一或四象限
C.在二或四象限 D.在一或三象限
【分析】根据xy>0,可得x>0,y>0或x<0,y<0,再根据各象限内点的坐标的符号特征判断即可.
【解析】∵xy>0,
∴x>0,y>0或x<0,y<0,
∴点P(x,y)在一或三象限.
故选:D.
9.(2020秋•未央区期中)如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(﹣3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为( )
A.(0,﹣3) B.(﹣1,﹣3) C.(3,0) D.(﹣2,0)
【分析】直接利用已知点坐标得出原点位置,进而得出答案.
【解析】如图所示:图书馆C的坐标为(﹣1,﹣3).
故选:B.
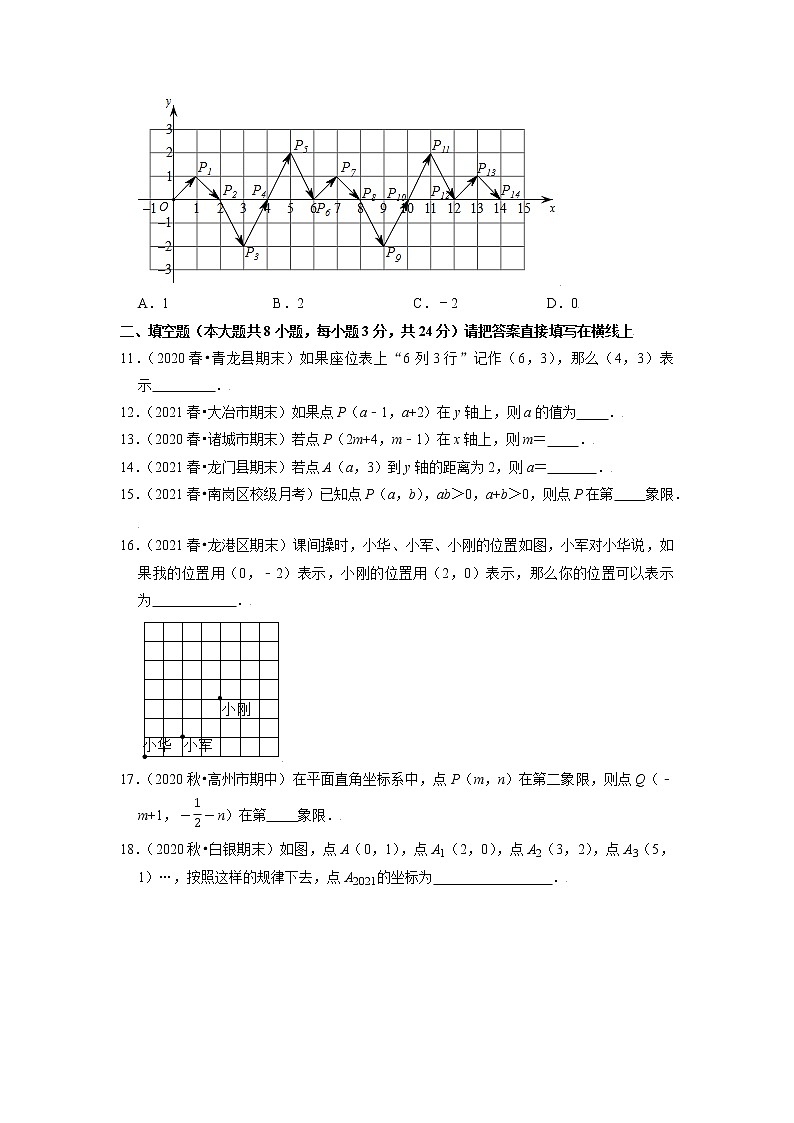
10.(2021春•赣州期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),…,按这样的运动规律,第2021次运动后,动点P2021的纵坐标是( )
A.1 B.2 C.﹣2 D.0
【分析】观察图象,结合第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),…,运动后的点的坐标特点,分别得出点P运动的横坐标和纵坐标的规律,再根据循环规律可得答案.
【解析】观察图象,结合第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),…,运动后的点的坐标特点,
由图象可得纵坐标每6运动组成一个循环:P1(1,1),P2(2,0),P3(3,﹣2),P4(4,0),P5(5,2),P6(6,0)…;
∵2021÷6=336…5,
∴经过第2021次运动后,动点P的坐标与P5坐标相同,为(5,2),
故经过第2021次运动后,动点P的纵坐标是2.
故选:B.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020春•青龙县期末)如果座位表上“6列3行”记作(6,3),那么(4,3)表示 4列3行 .
【分析】由题意得出第1个数字表示列、第2个数字表示行,据此可得.
【解析】∵座位表上“6列3行”记作(6,3),
∴(4,3)表示4列3行.
故答案为:4列3行.
12.(2021春•大冶市期末)如果点P(a﹣1,a+2)在y轴上,则a的值为 1 .
【分析】点在y轴上的条件是:横坐标是a﹣1=0,解方程即可得出结论.
【解析】∵点P(a﹣1,a+2)在y轴上,
∴a﹣1=0,
解得a=1.
故答案为:1.
13.(2020春•诸城市期末)若点P(2m+4,m﹣1)在x轴上,则m= 1 .
【分析】直接利用x轴上点的坐标特点为纵坐标为零,进而得出答案.
【解析】∵点P(2m+4,m﹣1)在x轴上,
∴m﹣1=0,
解得m=1,
故答案为:1.
14.(2021春•龙门县期末)若点A(a,3)到y轴的距离为2,则a= ±2 .
【分析】根据到y轴的距离等于横坐标的绝对值解答即可.
【解析】∵点A(a,3)到y轴的距离为2,
∴a=±2.
故答案为:=±2.
15.(2021春•南岗区校级月考)已知点P(a,b),ab>0,a+b>0,则点P在第 一 象限.
【分析】根据有理数的乘法、有理数的加法,可得a、b的符号,根据第一象限内点的横坐标大于零,纵坐标大于零,可得答案.
【解析】因为ab>0,a+b>0,
所以a>0,b>0,
点P(a,b)在第一象限,
故答案为:一.
16.(2021春•龙港区期末)课间操时,小华、小军、小刚的位置如图,小军对小华说,如果我的位置用(0,﹣2)表示,小刚的位置用(2,0)表示,那么你的位置可以表示为 (﹣2,﹣3) .
【分析】直接利用根据题意建立平面直角坐标系,进而得出小华的位置.
【解析】如图所示:小华的位置为:(﹣2,﹣3).
故答案为:(﹣2,﹣3).
17.(2020秋•高州市期中)在平面直角坐标系中,点P(m,n)在第二象限,则点Q(﹣m+1,-12-n)在第 四 象限.
【分析】先根据第二象限的点的横坐标为负数,纵坐标为正数求出m<0、n>0,然后确定出点Q的横坐标与纵坐标的正负情况,即可判断点Q所在的象限.
【解析】∵点P(m,n)是第二象限的点,
∴m<0、n>0,
∴﹣m>0,﹣n<0,
∴﹣m+1>0,-12-n<0,
∴点Q的坐标在第四象限.
故答案为:四.
18.(2020秋•白银期末)如图,点A(0,1),点A1(2,0),点A2(3,2),点A3(5,1)…,按照这样的规律下去,点A2021的坐标为 (3032,1010). .
【分析】观察图形得到奇数点的规律为,A1(2,0),A3(5,1),A5(8,2),…,A2n﹣1(3n﹣1,n﹣1),由2019是奇数,且2021=2n﹣1,则可求A2n﹣1(3032,1010).
【解析】观察图形可得,A1(2,0),A3(5,1),A5(8,2),…,A2n﹣1(3n﹣1,n﹣1),
A2(3,2),A4(6,3),A6(9,4),…,A2n(3n,n+1),
∵2021是奇数,且2021=2n﹣1,
∴n=1011,
∴A2n﹣1(3032,1010),
故答案为(3032,1010).
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020春•原州区期末)这是一所学校的平面示意图,建立适当的平面直角坐标系,并用坐标表示校门、图书馆、教学楼、旗杆和实验楼的位置.
【分析】直接建立平面直角坐标系进而得出各点的坐标.
【解析】如图所示:校门(0,0)、图书馆(0,3)、教学楼(3,2)、旗杆(4,0)、实验楼(2,﹣3).
20.建立直角坐标系,解决以下问题:
(1)画出下列各点,并把各点依次连接成封闭图形.
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0).
(2)指出上面各点所在的象限或坐标轴.
(3)分别写出上面各点关于x轴,y轴和原点的对称点.
【分析】(1)建立直角坐标系,在直角坐标系中画出下列各点,并把各点依次连接成封闭图形即可;
(2)根据各点的特征指出各点所在的象限或坐标轴即可;
(3)根据关于x轴对称的点的横坐标相等、纵坐标互为相反数,关于y轴对称的点的纵坐标相等、横坐标互为相反数,关于原点对称的点的横坐标互为相反数、纵坐标互为相反数,可得答案.
【解析】(1)如图所示;
(2)A(﹣2,3)在第二象限,
B(2,3)在第一象限,
C(5,0)在x轴的正半轴上,
D(2,﹣3)在第四象限,
E(﹣2,﹣3)在第三象限,
F(﹣5,0)在x轴的负半轴上;
(3)A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于x轴的对称点分别为:(﹣2,﹣3),(2,﹣3),(5,0),(2,3),(﹣2,3),(﹣5,0);
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于y轴的对称点分别为:(2,3),(﹣2,3),(﹣5,0),(﹣2,﹣3),(2,﹣3),(5,0);
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于原点的对称点分别为:(2,﹣3),(﹣2,﹣3),(﹣5,0),(﹣2,3),(2,3),(5,0);
21.(2020春•桃江县期末)如图,△ABC的三个顶点坐标分别为A(0,2),B(﹣3,1),C(﹣2,﹣2).
(1)将△ABC向右平移2个单位,作出△A'B'C';
(2)写出△A'B'C'的顶点坐标.
【分析】(1)分别作出A,B,C的对应点A′,B′,C′即可.
(2)根据A′,B′,C′的位置写出坐标即可.
【解析】(1)如图,△A'B'C'即为所求.
(2)A′(2,2),B′(﹣1,1),C′(0,﹣2).
22.(2021春•西城区校级期中)已知点A(3a﹣6,a+1),试分别根据下列条件,求出点A的坐标,
(1)点A在x轴上;
(2)点A在过点P(3,﹣2),且与y轴平行的直线上.
【分析】(1)根据x轴上点的纵坐标为0列方程求出a的值,再求解即可;
(2))根据平行于y轴的直线上的点的纵坐标相同列方程求出a的值,再求解即可.
【解析】(1)∵点A(3a﹣6,a+1)在x轴上,
∴a+1=0,
解得a=﹣1,
∴3a﹣6=﹣3﹣6=﹣9,
∴点A的坐标为(﹣9,0);
(2)∵点A在过点P(3,﹣2),且与y轴平行的直线上,
∴3a﹣6=3,
解得a=3,
∴a+1=3+1=4,
∴点A的坐标为(3,4).
23.(2021春•宜城市期末)如图,在平面直角坐标系xOy中,A、B、C三点的坐标分别为(﹣5,4)、(﹣3,0)、(0,2).
(1)画出三角形ABC,并求其面积;
(2)如图,△A′B′C′是由△ABC经过怎样的平移得到的?
(3)已知点P(a,b)为△ABC内的一点,则点P在△A′B′C′内的对应点P′的坐标( a+4 , b﹣3 ).
【分析】(1)根据A,B,C的坐标作出图形即可.
(2)根据平移变换的规律解决问题即可.
(3)利用平移规律解决问题即可.
【解析】(1)如图,△ABC即为所求.
S△ABC=4×5-12×2×4-12×2×5-12×2×3=8;
(2)先向右平移4个单位,再向下平移3个单位.
(3)由题意P′(a+4,b﹣3).
故答案为:a+4,b﹣3.
24.(2020春•广宁县期末)如图是某学校的平面示意图,已知旗杆的位置是(﹣2,3),实验室的位置是(1,4).
(1)画出图中的直角坐标系;
(2)写出图中食堂、图书馆的位置;
(3)已知办公楼的位置是(﹣2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
(4)如果一个单位长度表示30米,请求出宿舍楼到教学楼的实际距离.
【分析】(1)根据旗杆的坐标可以得到原点的位置,建立平面直角坐标系即可;
(2)写出这两点的坐标即可;
(3)根据坐标,描出点的位置即可;
(4)宿舍楼到教学楼的距离是8个单位长度,乘以30m即可.
【解析】(1)直角坐标系如图所示;
(2)食堂(﹣5,5)、图书馆(2,5);
(3)如图所示;
(4)由图可知宿舍楼到教学楼的实际距离为8×30=240(m).
25.(2019秋•台山市期中)如图是一个平面直角坐标系,按要求完成下列各小题.
(1)写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标;
(2)说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?
(3)写出点E关于y轴的对称点E′的坐标,并指出点E′与点C有怎样的位置关系.
【分析】(1)根据平面直角坐标系写出各点的坐标即可;
(2)根据点的坐标并结合图形解答即可;
(3)根据图形写出点E′的坐标,再根据关于原点对称的点的坐标特征解答.
【解析】(1)点A的坐标为(﹣2,0),点B的坐标为(0,﹣3),点D的坐标为(4,0),点F的坐标为(0,3);
(2)点B与点C的纵坐标相等,线段BC平行于x轴;
(3)点E关于y轴的对称点的坐标为(﹣3,3),它与点C关于原点对称.
26.(2018春•天心区校级期中)对于平面直角坐标系中任一点(a,b),规定三种变换如下:
①A(a,b)=(﹣a,b).如:A(7,3)=(﹣7,3);
②B(a,b)=(b,a).如:B(7,3)=(3,7);
③C(a,b)=(﹣a,﹣b).如:C(7,3)=(﹣7,﹣3);例如:A(B(2,﹣3))=A(﹣3,2)=(3,2)
规定坐标的部分规则与运算如下:
①若a=b,且c=d,则(a,c)=(b,d);反之若(a,c)=(b,d),则a=b,且c=d.
②(a,c)+(b,d)=(a+b,c+d);
(a,c)﹣(b,d)=(a﹣b,c﹣d).
例如:A(B(2,﹣3))+C(B(2,﹣3))=A(﹣3,2)+C(﹣3,2)=(3,2)+(3,﹣2)=(6,0).
请回答下列问题:
(1)化简:A(C(5,﹣3))= (5,3) (填写坐标);
(2)化简:C(A(﹣3,﹣2))﹣B(C(﹣1,﹣2))= (﹣5,1) (填写坐标);
(3)若A(B(2x,﹣kx))﹣C(A(1+y,﹣2))=C(B(ky﹣1,﹣1))+A(C(y,x)),且k为整数,点P(x,y)在第四象限,求满足条件的k的所有可能取值.
【分析】根据新定义进行化简即可.
【解析】(1)A(C (5,﹣3))=A(﹣5,3)=(5,3);
故答案为:(5,3);
(2)C(A(﹣3,﹣2))﹣B(C(﹣1,﹣2))
=C(3,﹣2)﹣B(1,2)
=(﹣3,2)﹣(2,1)
=(﹣5,1);
故答案为:(﹣5,1);
(3)A(B (2x,﹣kx))﹣C(A(1+y,﹣2))=C(B(ky﹣1,﹣1))+A(C(y,x)),
A(﹣kx,2x)﹣C(﹣1﹣y,﹣2)=C(﹣1,ky﹣1)+A(﹣y,﹣x)
(kx,2x)﹣(1+y,2)=(1,﹣ky+1)+(y,﹣x)
(kx﹣1﹣y,2x﹣2)=(1+y,1﹣ky﹣x)
∴kx﹣1﹣y=1+y且2x﹣2=1﹣ky﹣x,
∴2y=kx-23x=3-ky,
即y=kx-22x=3-ky3,
k=2y+2xk=3-3xy,
∵k为整数,点P(x,y)在第四象限,
∴x>0,y<0,
∴k=﹣2,﹣1,0,1,
沪科版八年级下册第18章 勾股定理综合与测试单元测试习题: 这是一份沪科版八年级下册第18章 勾股定理综合与测试单元测试习题,文件包含专题186第18章勾股定理单元测试能力过关卷解析版docx、专题186第18章勾股定理单元测试能力过关卷原卷版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
初中数学沪科版九年级上册第22章 相似形综合与测试单元测试课堂检测: 这是一份初中数学沪科版九年级上册第22章 相似形综合与测试单元测试课堂检测,文件包含专题227第22章相似形单元测试能力过关卷解析版docx、专题227第22章相似形单元测试能力过关卷原卷版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
八年级上册第11章 平面直角坐标系综合与测试单元测试课后作业题: 这是一份八年级上册第11章 平面直角坐标系综合与测试单元测试课后作业题,文件包含专题119第11章平面直角坐标系单元测试能力过关卷解析版docx、专题119第11章平面直角坐标系单元测试能力过关卷原卷版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。













