新疆乌鲁木齐市沙依巴克区2022-2023学年八年级上学期期中数学试卷(含答案)

这是一份新疆乌鲁木齐市沙依巴克区2022-2023学年八年级上学期期中数学试卷(含答案)，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
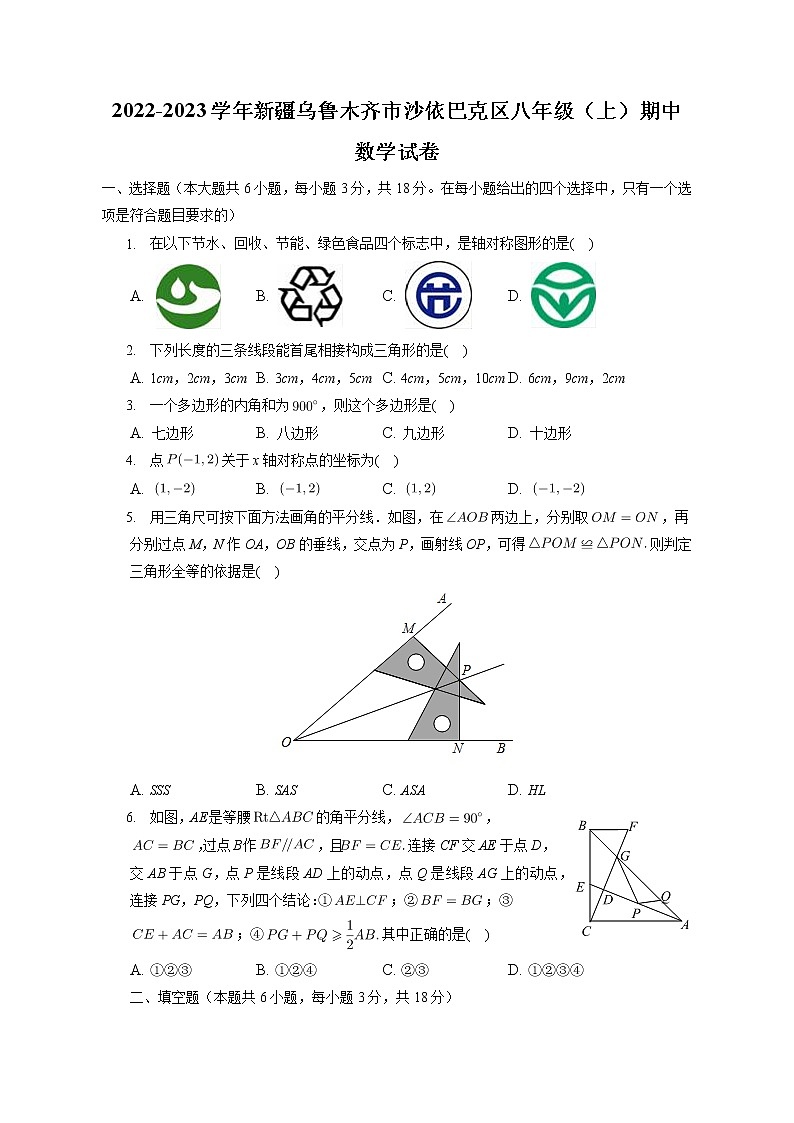
2022-2023学年新疆乌鲁木齐市沙依巴克区八年级（上）期中数学试卷一、选择题（本大题共6小题，每小题3分，共18分。在每小题给出的四个选择中，只有一个选项是符合题目要求的）    在以下节水、回收、节能、绿色食品四个标志中，是轴对称图形的是(    )A.  B.  C.  D.     下列长度的三条线段能首尾相接构成三角形的是(    )A. 1cm，2cm，3cm B. 3cm，4cm，5cm C. 4cm，5cm，10cm D. 6cm，9cm，2cm    一个多边形的内角和为，则这个多边形是(    )A. 七边形 B. 八边形 C. 九边形 D. 十边形    点关于x轴对称点的坐标为(    )A.  B.  C.  D.     用三角尺可按下面方法画角的平分线．如图，在两边上，分别取，再分别过点M，N作OA，OB的垂线，交点为P，画射线OP，可得≌则判定三角形全等的依据是(    )
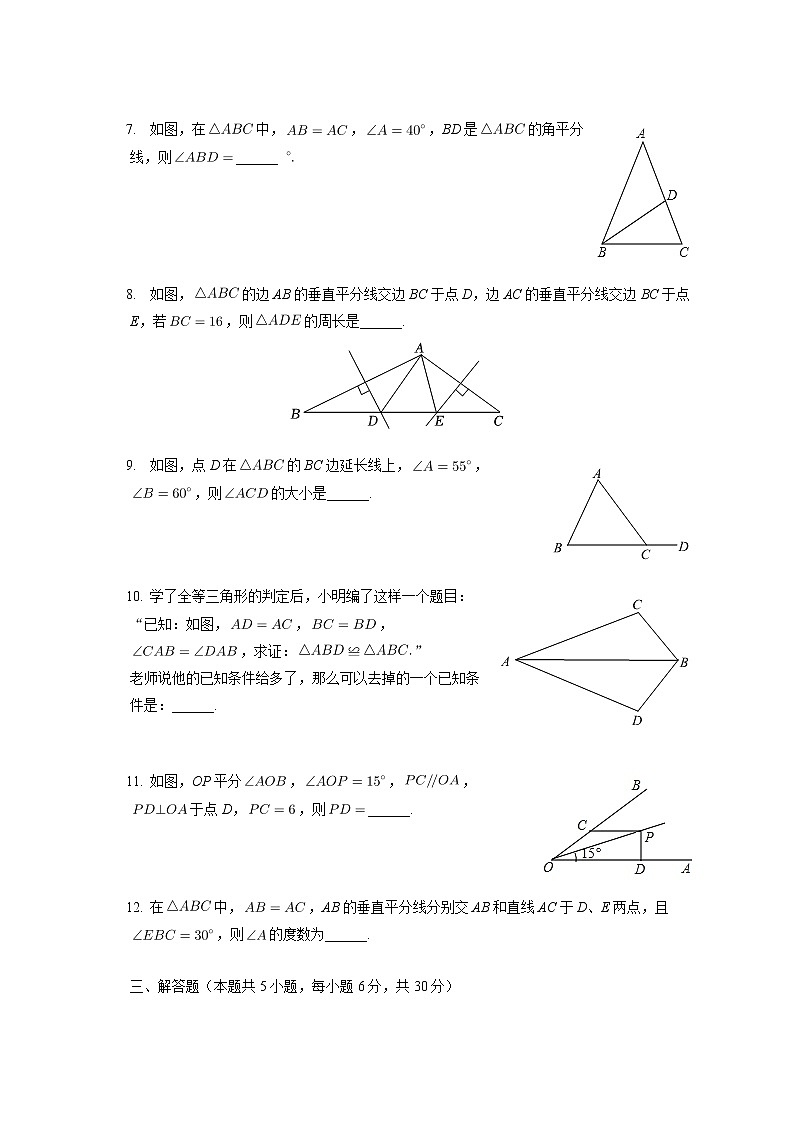
A. SSS B. SAS C. ASA D. HL    如图，AE是等腰的角平分线，，，过点B作，且连接CF交AE于点D，交AB于点G，点P是线段AD上的动点，点Q是线段AG上的动点，连接PG，PQ，下列四个结论：①；②；③；④其中正确的是(    )A. ①②③ B. ①②④ C. ②③ D. ①②③④二、填空题（本题共6小题，每小题3分，共18分）     如图，在中，，，BD是的角平分线，则______
     如图，的边AB的垂直平分线交边BC于点D，边AC的垂直平分线交边BC于点E，若，则的周长是______.
    如图，点D在的BC边延长线上，，，则的大小是______.
 学了全等三角形的判定后，小明编了这样一个题目：“已知：如图，，，，求证：≌”
老师说他的已知条件给多了，那么可以去掉的一个已知条件是：______.
 如图，OP平分，，，于点D，，则______.
 在中，，AB的垂直平分线分别交AB和直线AC于D、E两点，且，则的度数为______. 三、解答题（本题共5小题，每小题6分，共30分） 如图，点B，E，C，F在同一条直线上，，，，求证：
如图，在中，D为BC延长线上一点，于F，交AC于E，若，，求的度数．
 已知，如图，，，于点E，于点F，求证：
在如图所示的正方形网格中建立平面直角坐标系，的顶点坐标分别为，，，请按要求解答下列问题：
画出关于x轴对称的，并写出点A的对应点的坐标为______，______；
平行于y轴的直线l经过，画出关于直线l对称的图形，并写出的坐标为______，______
如图所示，在中，，DE垂直平分AB，交BC于点E，垂足为点D，，，求 
四、（本题共3小题，每小题8分，共24分）如图，为等腰直角三角形，，
求证：≌；
求证：
如图，在中，，点D、E、F分别在AB、BC、AC边上，且，
 求证：是等腰三角形；当时，求的度数． 如图，在中，，DE垂直平分AB，交边AB于点D，交边AC于点E，BF垂直平分CE，交AC于点F，连接
求证：；
求的度数．
五、（本题共2小题，每小题9分，共18分）如图，在中，，AE平分
若，求的度数．
证明：
在学习完第十二章后，张老师让同学们独立完成课本56页第9题：“如图1，，，，，垂足分别为D，E，，，求BE的长．”
请你也独立完成这道题；
待同学们完成这道题后，张老师又出示了一道题：
在课本原题其它条件不变的前提下，将CE所在直线旋转到的外部如图，请你猜想AD，DE，BE三者之间的数量关系，直接写出结论，不需证明；
如图3，将中的条件改为：在中，，D，C，E三点在同一条直线上，并且有，其中为任意钝角，那么中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．
 六、（本大题12分） 如图①，在等边中，点D、E分别是AB、AC上的点，，BE与CD交于点
填空：______度；
如图②，以CO为边作等边，AF与BO相等吗？并说明理由；
如图③，若点G是BC的中点，连接AO、GO，判断AO与GO有什么数量关系？并说明理由．

答案和解析 1.【答案】D 【解析】解：A、不是轴对称图形，故此选项错误；
B、不是轴对称图形，故此选项错误；
C、不是轴对称图形，故此选项错误；
D、是轴对称图形，故此选项正确．
故选：
2.【答案】B 【解析】解：根据三角形的三边关系，得：
A、，不能构成三角形；
B、，能构成三角形；
C、，不能构成三角形；
D、，不能构成三角形．
故选：
3.【答案】A 【解析】解：设多边形的边数为n，
，解得：故选：
4.【答案】D 【解析】解：点关于x轴对称的点的坐标为，
故选：
5.【答案】D 【解析】解：在和中，
，
，故选：
6.【答案】D 【解析】解：，
，
，
又，，
≌，
，
，，，
，故①正确；
平分，，，
，，，故②正确；
，，故③正确；
如图，连接PC，CQ，过点C作于H，

，，，
，，，
是CG的中垂线，，
，点Q是线段AG上的动点，
，，故选：
7.【答案】35 【解析】解：，，
，
又为的平分线，，故答案为：
8.【答案】16 【解析】解：边AB的垂直平分线交边BC于点D，边AC的垂直平分线交边BC于点E，
，，
，
的周长
，故答案为：
9.【答案】 【解析】解：是的外角，，，
，
故答案为：
10.【答案】或 【解析】解：可以去掉的一个已知条件是：或，
理由：在和中，
，
≌
在和中，
，
≌
可去掉的条件是或
故答案为：或
11.【答案】3 【解析】解：如图，过点P作于E，
平分，
，
，
，
，
平分，，，

故答案为：
12.【答案】或 【解析】解：如图1，

，
，，
垂直且平分AB，，，
，
，
解得；
如图2，

，
，
垂直且平分AB，
，
，
，
，
，
解得，

故答案为：或
13.【答案】证明：已知，
，
即，
在和中，
，
≌，
全等三角形对应边相等 14.【答案】解：
，
，
，

所以的度数为。 15.【答案】证明：如图，连接AD，

在和中，
，
≌，
，
又，，
 16.【答案】 【解析】解：如图，即为所求；
的坐标为；
故答案为：，；

如图，即为所求；
的坐标为
故答案为：7，17.【答案】解：在中，，，
，
垂直平分AB，，
，
，
，
，
，
 18.【答案】证明：是等腰直角三角形，
，
，
，
，
在与中，
，
≌
证明：≌，
，，
，，
， 19.【答案】证明：，
，
在和中
，
≌，，是等腰三角形；
如图，

≌，
，，
，



 20.【答案】证明：垂直平分AB，，
垂直平分CE，，；
解：，，
，，
，，，
设，，
，，
，，
解得：，即 21.【答案】解：，

平分，

，
，


于D，

平分，

，

，


 22.【答案】解：，，


，

在和中，

≌
，
，，



中的猜想还成立
证明：，，，

在和中，

≌
，
 23.【答案】
解：结论：
理由：如图②中，

，都是等边三角形，
，，，

即，
在和中，
，
≌，

解：如图③中，结论：
理由：延长OG到R，使得，连接CR，

点G是BC的中点，

在和中，
，
≌，
，，
，
≌，
，，
，
，
，
，
，
在和中，
，
≌，
，
，
 【解析】解：如图①中，

是等边三角形，
，，
在和中，
，
≌，
，
，

故答案为：