高中数学人教B版 (2019)必修 第二册6.2.2 直线上向量的坐标及其运算背景图课件ppt

这是一份高中数学人教B版 (2019)必修 第二册6.2.2 直线上向量的坐标及其运算背景图课件ppt，文件包含人教B版高中数学必修第二册第6章62622直线上向量的坐标及其运算课件ppt、人教B版高中数学必修第二册第6章62622直线上向量的坐标及其运算学案doc、人教B版高中数学必修第二册课后素养落实26直线上向量的坐标及其运算含答案doc等3份课件配套教学资源，其中PPT共39页， 欢迎下载使用。
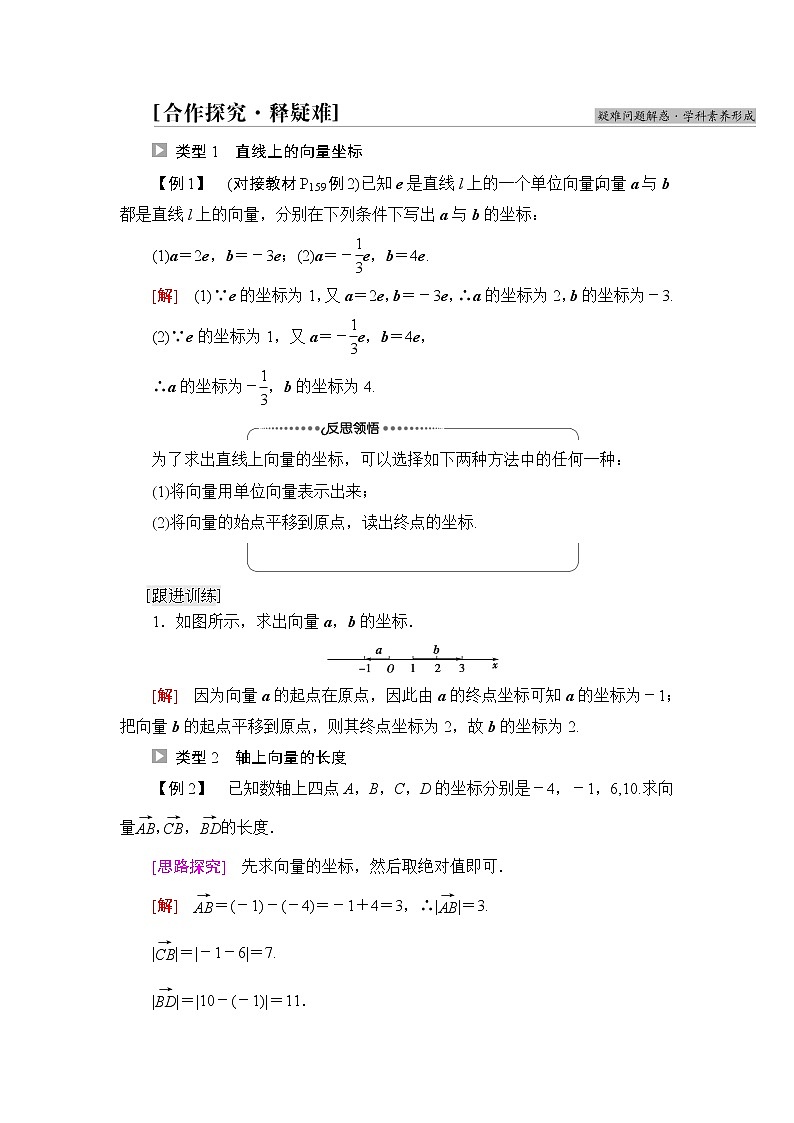
6.2.2　直线上向量的坐标及其运算学 习 任 务核 心 素 养(教师独具)1．了解直线上向量的坐标的概念，能够表示直线上向量的坐标．(重点)2．理解直线上向量的运算与坐标的关系，并能进行正确的运算．(难点)1．借助直线上向量的坐标表示，培养数学抽象的核心素养．2．通过直线上向量的运算与坐标的关系，提升数学运算的核心素养.我们在必修第一册上已学过了数轴上点的坐标，如图，已知A(－1)，B(2)．问题：(1)对应的向量坐标是多少？(2)对应的向量坐标是多少？[提示]　(1)3.(2)－3.知识点1　直线上向量的坐标1．定义给定一条直线l以及这条直线上一个单位向量e，对于直线l上的任意一个向量a，一定存在唯一的实数x，使得a＝xe，此时，x称为向量a的坐标．2．向量a的坐标为x，与|a|的关系|a|＝|xe|＝|x||e|＝|x|.当x＞0时，a的方向与e的方向相同；当x＝0时，a是零向量；当x＜0时，a的方向与e的方向相反．3．记法如果数轴上一点A对应的数为x(记为A(x)，也称点A的坐标为x)，那么向量对应的坐标为x；反之，这一结论也成立．1．已知数轴上两点A，B的坐标分别是20，－15，则向量的坐标是(　　)A．－35 B．5　　　C．35　　　 D．－5A　[＝－15－20＝－35.]2.设数轴上A，B的坐标分别是2,6，则AB的中点C的坐标是________．4　[∵xA＝2，xB＝6，∴AB中点C的坐标为xC＝＝＝4.]知识点2　直线上向量的运算与坐标的关系1．向量相等与两向量的和假设直线上两个向量a，b的坐标分别为x1，x2，即a＝x1e，b＝x2e.当a＝b时，有x1e＝x2e，由e是单位向量可知x1＝x2，也就是直线上两个向量相等的充要条件是它们的坐标相等．a＋b＝x1＋x2，这就是说，直线上两个向量和的坐标等于两个向量的坐标的和．2．数轴上两点的坐标公式与距离公式在数轴x上，点A的坐标为x1，点B的坐标为x2，则＝x2－x1．AB＝||＝|x2－x1|.3.已知数轴上A，B，C三点，若＝2，＝3，则的坐标为(　　)A．－5　 B．－1　　　　C．1　　　　 D．5D　[＝＋＝5.]4.已知e为λ上的单位向量，a＝－2e，b＝8e，则c＝8a＋5b的坐标为________．24　[向量c的坐标为(－2)×8＋5×8＝24.] 类型1　直线上的向量坐标【例1】　(对接教材P159例2)已知e是直线l上的一个单位向量，向量a与b都是直线l上的向量，分别在下列条件下写出a与b的坐标：(1)a＝2e，b＝－3e；(2)a＝－e，b＝4e.[解]　(1)∵e的坐标为1，又a＝2e，b＝－3e，∴a的坐标为2，b的坐标为－3.(2)∵e的坐标为1，又a＝－e，b＝4e，∴a的坐标为－，b的坐标为4.为了求出直线上向量的坐标，可以选择如下两种方法中的任何一种：1将向量用单位向量表示出来；2将向量的始点平移到原点，读出终点的坐标.1．如图所示，求出向量a，b的坐标．[解]　因为向量a的起点在原点，因此由a的终点坐标可知a的坐标为－1；把向量b的起点平移到原点，则其终点坐标为2，故b的坐标为2. 类型2　轴上向量的长度【例2】　已知数轴上四点A，B，C，D的坐标分别是－4，－1，6,10.求向量，，的长度．[思路探究]　先求向量的坐标，然后取绝对值即可．[解]　＝(－1)－(－4)＝－1＋4＝3，∴||＝3.||＝|－1－6|＝7.||＝|10－(－1)|＝11．求轴上向量长度的方法要先求轴上向量的坐轴，再根据距离公式求长度．提醒：首先利用数轴上点的坐标，计算出两点所对应向量的坐标，特别要注意向量坐标运算公式的顺序．2．已知A，B，C为数轴上三点，且xA＝－2，xB＝6.试求符合下列条件的点C的坐标．(1)AC＝10；(2)||＝10；(3)||＝3||.[解]　(1)∵AC＝10，∴xC－xA＝10.∴xC＝xA＋10＝8.(2)∵||＝10，∴AC＝10或AC＝－10，当AC＝10时，xC－xA＝10，xC＝xA＋10＝8；当AC＝－10时，xC－xA＝－10，xC＝xA－10＝－12.(3)∵||＝3||，∴＝3或＝－3.当＝3时，xC－xA＝3(xC－xB)．∴xC＝(3xB－xA)＝10；当＝－3时，xC－xA＝－3(xC－xB)，∴xC＝(3xB＋xA)＝4. 类型3　直线上的向量坐标运算及其应用【例3】　已知直线上的向量a与向量b，向量a的坐标为－10，向量a与向量b满足关系2a－3b＝4，求：(1)向量b的坐标；(2)a＋2b的坐标．[解]　(1)设直线上的向量b的坐标为x，由题意可得2×(－10)－3x＝4，解得x＝－8，即向量b的坐标为－8.(2)a＋2b＝－10＋2×(－8)＝－26，所以a＋2b的坐标为－26.求向量坐标：终点坐标减去起点坐标.,求向量长度：先求向量坐标，然后取绝对值.3．已知数轴上四点A，B，C，D的坐标分别是－4，－2，c，d.(1)若AC＝5，求c的值；(2)若||＝6，求d的值．[解]　(1)∵＝5，∴c－(－4)＝5，∴c＝1．(2)∵|BD|＝6，∴|d－(－2)|＝6，即d＋2＝6或d＋2＝－6，∴d＝4或d＝－8.1．设e1，e2是两个单位向量，则下列结论中正确的是(　　)A．e1＝e2　　　　　　 B．e1∥e2C．|e1|＝|e2| D．以上都不对C　[单位向量的模都等于1个单位，故C项正确．]2．已知数轴上两点A，B的坐标分别是－4，－1，则与AB分别是(　　)A．－3,3 B．3,3C．3，－3 D．－6,6B　[＝－1－(－4)＝3，AB＝||＝3.]3．已知数轴上两点A，B的坐标分别是－9,3，则＝(　　)A．－6 B．6C．12 D．－12C　[＝3－(－9)＝12.]4．数轴上点A(－3)关于点M(2)的对称点为B(x)，则x＝________.7　[由题意可得2＝，解得x＝7.]5．已知a，b是直线上的向量，a的坐标为1，且|3a－2b|＝1，则b的坐标为________．1或2　[设b的坐标为x，则|3×1－2x|＝1，即3－2x＝±1，∴x＝1或x＝2，即向量b的坐标为1或2.]回顾本节内容，自我完成以下问题：1．直线上向量的起点都认为起点为原点O，则直线上的向量与直线上的点是一一对应吗？[提示]　一一对应．2．向量a的坐标x能刻画它的模与方向吗？[提示]　能．(1)|a|＝|xe|＝|x||e|＝|x|.(2)当x＞0时，a的方向与e的方向相同；当x＝0时，a是零向量；当x＜0时，a的方向与e的方向相反．