2022-2023学年江苏省无锡市江阴市澄西片八年级（上）期中数学试卷（含解析）

2022-2023学年江苏省无锡市江阴市澄西片八年级（上）期中数学试卷

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

第I卷（选择题）

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列四个图案中，是轴对称图形的是(    )

A.  B.  C.  D.

2. 如图，要说明≌，需添加的条件不能是(    )

A.  B.  C.  D.

3. 等腰三角形的周长为，其中一边长为则该等腰三角形的底长为(    )

A.  或  B.  或  C.   D.  

4. 在联合会上，有、、三名选手站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在的(    )

A. 三边中线的交点 B. 三条角平分线的交点
C. 三边中垂线的交点 D. 三边上高的交点

5. 下列说法中，不一定正确的是(    )

A. 角是轴对称图形，对称轴是角的平分线
B. 等腰三角形至少有条对称轴，至多有条对称轴
C. 关于某直线对称的两个三角形一定是全等三角形
D. 一条直角边和斜边相等的两个直角三角形全等

6. 在正方形网格中，的位置如图所示，到两边距离相等的格点应是(    )

A. 点
B. 点
C. 点
D. 点

7. 如图，中，，为的中点，，若，，则的长为(    )

A.
B.
C.
D.

8. 如图，在正方形中，是的中点，将沿翻折至，连接，则与互余的角有(    )

A. 个
B. 个
C. 个
D. 个

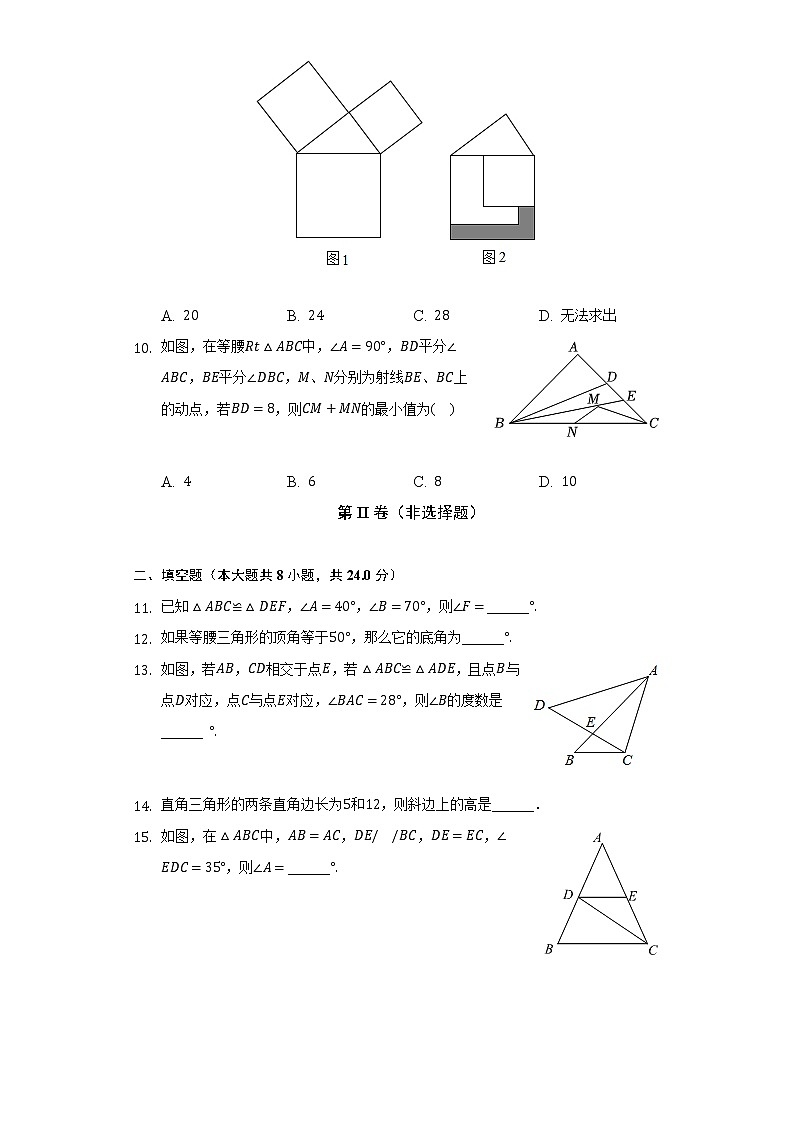
9. 勾股定理是人类最伟大的科学发现之一，在我国古算书周髀算经中早有记载，如图，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图的方式放置在最大的正方形内，若直角三角形两直角边分别为和，则图中阴影部分的面积为(    )

A.  B.  C.  D. 无法求出

10. 如图，在等腰中，，平分，平分，、分别为射线、上的动点，若，则的最小值为(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共8小题，共24.0分）

11. 已知≌，，，则______
12. 如果等腰三角形的顶角等于，那么它的底角为______
13. 如图，若，相交于点，若≌，且点与点对应，点与点对应，，则的度数是______

14. 直角三角形的两条直角边长为和，则斜边上的高是______．
15. 如图，在中，，，，，则______

16. 如图，在四边形中，，，平分，且，点为边中点，，则的面积为______．

17. 算法统宗是中国古代数学名著，作者是我国明代数学家程大位．在算法统宗中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几？”译文：“有一架秋千，当它静止时，踏板离地尺，将它往前推送尺水平距离时，秋千的踏板就和人一样高，这个人的身高为尺，秋千的绳索始终拉得很直如图所示，试问绳索有多长？”根据题意求出绳索的长为______尺．
18. 如图，在中，，，，分别为、为一直角边作等腰直角、，连接交的延长线于，则的面积为______．

三、解答题（本大题共8小题，共66.0分。解答应写出文字说明，证明过程或演算步骤）

19. 本小题分
    如图，已知，，、是上两点，且求证：≌．

20. 本小题分
    如图，，的垂直平分线交于，交于．
    若，求的度数；
    若，的周长为，求的周长．

21. 本小题分
    如图，四边形中，，为的中点，连结并延长交的延长线于点．
    求证：≌；
    连结，当，，时，求的长．

22. 本小题分
    如图，在中，，，，点是外一点，连接，，且，求：四边形的面积．

23. 本小题分
    如图，请用无刻度直尺在以下网格图中按要求作图．
    如图，四边形的顶点都在格点上，请在边上找一点，使得；
    如图，点、、均为格点，请过点画出所有满足条件的直线，使得点、到直线的距离相等．
24. 本小题分
    如图，长方形，把长方形沿对角线折叠，使点落在点处，交于点．
    请证明点在线段的垂直平分线上；
    若，，求的长．

25. 本小题分
    如图，正方形的边长为，点在边上，，动点从点出发，以的速度沿运动，设运动时间为秒．
    
    ______；
    当点在的垂直平分线上时，求的值；
    当______，平分，试猜想此时是否为的角平分线，并说明理由．
26. 本小题分
    定义：在中，若，，，，，满足则称这个三角形为“类勾股三角形”请根据以上定义解决下列问题：
    
    命题：“直角三角形都是类勾股三角形”是______填“真”或“假”命题．
    如图所示、若等腰三角形是“类勾股三角形”，其中，，请求的度数．
    如图所示，在中，，且．
    当时，你能把这一个三角形分成两个等腰三角形吗？若能，请在图中画出分割线，并标注被分割后的两个等腰三角形的顶角的度数；若不能，请说明理由．
    请证明为“类勾股三角形”．
    

答案和解析

1.【答案】 

【解析】解：选项A、、不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
选项D能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
故选：．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 

2.【答案】 

【解析】解：、在和中

≌，故本选项不符合题意；
B、在和中

≌，故本选项不符合题意；
C、，
，
，
，
在和中

≌，
，
在和中

≌，故本选项不符合题意；
D、根据，，不能推出≌，故本选项符合题意；
故选：．
根据全等三角形的判定定理逐个判断即可．
本题考查了全等三角形的判定和性质，能灵活运用定理进行推理是解此题的关键，注意：全等三角形的判定定理有，，，．
 

3.【答案】 

【解析】

【分析】
本题考查了等腰三角形的性质，三角形的三边关系，难点在于分情况讨论，此类题目，要注意判断是否能组成三角形．
分是腰长时求出底边，是底边时求出腰长，再根据三角形的任意两边之和大于第三边判断是否能够组成三角形，从而得解．
【解答】
解：是腰长时，底边，
此时，三角形的三边分别为、、，
，
不能组成三角形；
是底边时，腰长，
此时，三角形的三边分别为、、，
能够组成三角形，
综上所述，该等腰三角形的底长为．
故选：．  

4.【答案】 

【解析】解：三角形的三条垂直平分线的交点到三角形各顶点的距离相等，
凳子应放在的三条垂直平分线的交点最适当．
故选：．
为使游戏公平，要使凳子到三个人的距离相等，于是利用线段垂直平分线上的点到线段两端的距离相等可知，要放在三边中垂线的交点上．
本题主要考查了线段垂直平分线的性质的应用；利用所学的数学知识解决实际问题是一种能力，要注意培养．想到要使凳子到三个人的距离相等是正确解答本题的关键．
 

5.【答案】 

【解析】解：角是轴对称图形，对称轴是角的平分线所在的直线，原说法错误，故本选项符合题意；
B.等腰三角形至少有条对称轴，至多有条对称轴，说法正确，故本选项不合题意；
C.关于某直线对称的两个三角形一定是全等三角形，说法正确，故本选项不合题意；
D.一条直角边和斜边相等的两个直角三角形全等，说法正确，故本选项不合题意；
故选：．
选项A根据轴对称图形的定义判断即可；选项B根据等腰三角形的性质以及轴对称图形的定义判断即可；选项C根据全等三角形的定义以及轴对称的性质判断即可；选项D根据直角三角形的判定方法判断即可．
本题考查了轴对称图形的定义与性质，等腰三角形的性质，全等三角形的判断以及直角三角形的判断，掌握相关定义与判定方法是解答本题的关键．
 

6.【答案】 

【解析】解：点到两边距离相等，
理由是：角平分线上的点到角两边的距离相等，
故选：．
根据角平分线的性质得出即可．
本题考查了角平分线的性质，能熟记角平分线性质是解此题的关键，注意：角平分线上的点到角两边的距离相等．
 

7.【答案】 

【解析】解：，
，
点为的中点，
，
，
在中，由勾股定理得：，
，
故选：．
由直角三角形斜边上的中线性质得，则，再由勾股定理得，即可解决问题．
本题考查了勾股定理、直角三角形斜边上的中线性质等知识，熟练掌握勾股定理和直角三角形斜边上的中线性质是解题的关键．
 

8.【答案】 

【解析】解：连接交于点，
四边形是正方形，
，
将沿翻折得到，
，，
点与点关于直线对称，
垂直平分，
，，
，
，
，
，
，
，
，
，
，；
，，
的余角有个，
故选：．
连接交于点，由四边形是正方形，得，由翻折得，，垂直平分，即可证明，再证明，则，，，，可知的余角有个．
此题重点考查正方形的性质、同角的余角相等、轴对称的性质、三角形的中位线定理等知识，正确地作出所需要的辅助线并且证明及是解题的关键．
 

9.【答案】 

【解析】解：将阴影部分分割如图所示：

根据直角三角形的三边为、、．
所以阴影部分的面积为．
故选：．
将阴影部分分割成正方形和长方形，根据直角三角形的边关系，即可求解．
本题考查的是正方形性质即四边相等；勾股定理，即两条直角边长分别是，，斜边长为，那么．
 

10.【答案】 

【解析】解：如图所示，作于交点，再作垂直于，过点作于点，

平分，平分，
，，
．
则的最小值为的长，
设，
，
，
，
，
，
，
，
，
，

，
故选：．
先作于交点，再作垂直于，根据角平分线的性质：角分线上的点到角的两边距离相等，即可找到动点和，进而求得的最小值．
本题考查了轴对称最短路线问题、角平分线的性质，解决本题的关键是找到使最小时的动点和．
 

11.【答案】 

【解析】解：，，
，
≌，
，
故答案是：．
根据三角形内角和定理求出，根据全等三角形的性质解答即可．
本题考查的是全等三角形的性质、三角形内角和定理，掌握全等三角形的对应角相等是解题的关键．
 

12.【答案】 

【解析】解：等腰三角形的顶角等于，
又等腰三角形的底角相等，
底角等于．
故答案为：．
利用等腰三角形的性质及三角形内角和定理直接可求得答案．
本题考查了三角形内角和定理和等腰三角形的性质，熟记等腰三角形的性质是解题的关键．
 

13.【答案】 

【解析】解：≌，且点与点对应，点与点对应，
，，，
，
，，
，，
，
，
故答案为．
由全等三角形的性质得到，，，由等腰三角形的性质和三角形内角和定理求出，再根据三角形内角和定理求出，即可得到的度数．
本题主要考查了全等三角形的性质，三角形内角和定理，等腰三角形的性质，熟练掌握全等三角形的性质是解决问题的关键．
 

14.【答案】 

【解析】解：在直角三角形中，已知两直角边为，，
则斜边长为，
根据面积法，直角三角形面积可以根据两直角边求值，也可以根据斜边和斜边上的高求值，
即可求得两直角边的乘积斜边长斜边上高线长，
斜边上的高线长，
故答案为：．
在直角三角形中，已知两直角边长为，，根据勾股定理可以计算斜边的长，根据三角形面积的不同方法计算可以求得斜边的高的长度．
本题考查了勾股定理在直角三角形中的运用，三角形面积的计算，根据面积法求斜边的高是解题的关键．
 

15.【答案】 

【解析】解：，，
，
，
，
，
，
，
．
故答案为：．
根据等腰三角形的性质可求得的度数，又由，求得的度数，可求的度数，然后由等腰三角形的性质和三角形内角和定理可求的度数．
此题考查了等腰三角形的性质，平行线的性质以及三角形内角和定理，注意掌握数形结合思想的应用．
 

16.【答案】 

【解析】解：如图，过作于，
，
，
平分，
，
，
，
点为边中点，，
，
，
故答案为：．
过作于，由角平分线的性质得，再由直角三角形斜边上的中线性质得，然后由三角形面积公式即可得出结论．
本题考查了角平分线的性质、直角三角形斜边上的中线性质以及三角形面积公式，熟练掌握角平分线的性质和直角三角形斜边上的中线性质是解题的关键．
 

17.【答案】 

【解析】解：设绳索有尺长，
则，
解得：，
即绳索长尺，
故答案为：．
设绳索有尺长，根据勾股定理列方程即可得到结果．
本题考查了勾股定理的应用、理解题意能力，关键是能构造出直角三角形，用勾股定理来解．
 

18.【答案】 

【解析】解：过作交于，
，
，
，
，
≌，
，，
，，
，，
四边形是平行四边形，
，
，
的面积为，
故答案为：．
过作交于，根据全等三角形的判定和性质以及平行四边形的判定和性质即可得到结论．
本题考查了全等三角形的判定和性质，平行四边形的判定和性质，正确地作出辅助线是解题的关键．
 

19.【答案】证明：，
，
，
，
即，
在和中，
，
≌． 

【解析】根据证明即可．
本题考查全等三角形的判定，平行线的性质等知识，解题的关键是根据平行线的性质得到．
 

20.【答案】解：
，
垂直平分
，
，
；
是的垂直平分线
，，
，
的周长，
的周长． 

【解析】先根据等腰三角形的性质求出，再由垂直平分可知，所以，再根据即可得出结论；
由是的垂直平分线可知，，，所以，再由的周长，可求出的周长．
本题考查的是等腰三角形的性质，线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
 

21.【答案】解：，
，，
点为的中点，
，
在和中，
，
≌；
≌，
，，
，
，
，
的长为． 

【解析】由“”可证≌；
由全等三角形的性质可得，，由中垂线的性质可得，可得结论；
本题考查了全等三角形的判定和性质，线段垂直平分线的性质，证明≌是本题的关键．
 

22.【答案】解：中，，，，
；
在中，，，，
，
是直角三角形，
四边形的面积． 

【解析】在中，根据勾股定理即可求得的长；再利用勾股定理逆定理即可证明是直角三角形，再根据三角形的面积公式可求四边形的面积．
本题考查了勾股定理及其逆定理．勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．勾股定理的逆定理：如果三角形的三边长，，满足，那么这个三角形就是直角三角形．掌握定理是解题的关键．
 

23.【答案】解：如图中，点即为所求；
如图中，直线，直线即为所求．
 

【解析】连接，作出线段的垂直平分线交于点，连接，点即为所求；
取格点，作直线，连接取的中点，作直线即可．
本题考查作图应用与设计作图，线段的垂直平分线的性质，勾股定理等知识，解题的关键是掌握线段的垂直平分线的性质，属于中考常考题型．
 

24.【答案】证明：四边形是矩形，
，
，
由折叠得，
，
，
点在线段的垂直平分线上．
解：设，
，
，
，
，
，且，
，
解得，
，
的长是． 

【解析】先证明，得，则点在线段的垂直平分线上；
设，则，因为，所以，由，且，得，解方程求出的值即可．
此题重点考查矩形的性质、轴对称的性质、等腰三角形的判定、到线段两端距离相等的点在线段的垂直平分线上、勾股定理等知识，证明是解题的关键．
 

25.【答案】   

【解析】解：四边形是正方形，
，
，
故答案为：；

如图中，设的垂直平分线交于点，交于点，连接过点作于点．

由题意，
在中，则有，
．
，
四边形是矩形，
，，
，，，
，
≌，
，
，
运动到时，，
综上所述，满足条件的的值为或．

结论：是的角平分线．
理由：如图中，连接，过点作于点．

平分，，
，，
，
≌，
，，
，
，
，，
≌，
，
，
，，
，
平分，
，
．
故答案为：．
利用勾股定理求解即可；
如图中，设的垂直平分线交于点，交于点，连接过点作于点由题意，利用勾股定理求出，再证明，求出，可得结论；
结论：是的角平分线．如图中，连接，过点作于点利用全等三角形的性质证明，可得结论．
本题考查正方形的性质，全等三角形的判定和性质，角平分线的判定定理等知识，解题的关键是学会利用参数构建方程解决问题，学会添加常用辅助线，构造全等三角形解决问题．
 

26.【答案】假 

【解析】解：如图，假设是类勾股三角形，
，
在中，，根据勾股定理得，，
，
，
，
是等腰直角三角形，
等腰直角三角形是类勾股三角形，
即：原命题是假命题，
故答案为：假；

，，
，，
是类勾股三角形
，
，
是等腰直角三角形，
，

在中，，，
，
根据三角形的内角和定理得，，
把这个三角形分成两个等腰三角形，
Ⅰ、分割线分，
Ⅰ、当时，
，
，
，
不是等腰三角形，此种情况不成立；
Ⅱ、当时，
，
，
是等腰三角形，此种情况不成立；
Ⅲ、当时，
．
是等腰三角形，
图形如图所示：两个等腰三角形的顶角的度数分别为和．

Ⅱ、分割线分，同Ⅰ的方法，判断此种情况不成立；
Ⅲ、分割线分，同Ⅱ的方法，判断此种情况不成立；

如图，在边上取点，连接，使，作于，

，
，
，
，
，
，
，

，
，
在中，，
在中，，
，
，
是“类勾股三角形”．
先由直角三角形是类勾股三角形得出，再由勾股定理得，即可判断出此直角三角形是等腰直角三角形；
由类勾股三角形的定义判断出此三角形是等腰直角三角形，即可得出结论；
分三种情况，利用等腰三角形的性质即可得出结论；
先求出，，，，，两个直角三角形中利用勾股定理建立方程即可得出结论．
本题考查等腰三角形的判定和性质，勾股定理，“类勾股三角形”的定义等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考常考题型．